Линейные однофазные синусоидальные электрические цепи с параллельным и смешанным соединением элементов цепи

123

Во многих случаях приходится встречаться с расчётом сложных электрических цепей синусоидального тока, которые в общем случае являются цепями со смешанным соединением сопротивлений (рис. 2.1). Эти электрические цепи могут быть разделены на участки с последовательным и участки с параллельным соединением сопротивлений.

При параллельном соединении сопротивлений (участок 1 − 2, рис. 2.1) параллельные ветви электрической цепи находятся под одним и тем же напряжением U₁ = U₁₂, поэтому для каждой из этих ветвей определение всех расчётных величин производится по формулам, справедливым для отдельных сопротивлений электрических цепей с последовательным соединением сопротивлений. Для участка цепи с параллельным соединением сопротивлений ток на разветвлённом участке определяется в соответствии с I законом Кирхгофа, записанным для узла разветвления в векторной форме:

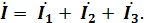
Этот ток можно определить графически с помощью векторной диаграммы как сумму составляющих векторов токов, а также с помощью комплексных чисел, так как комплексный ток ,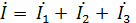

т. е. равен сумме комплексных составляющих токов.

Комплексы токов в отдельных ветвях электрической цепи могут быть определены через комплексные сопротивления или комплексные проводимости соответствующих ветвей:

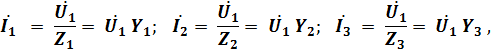
где в общем случае

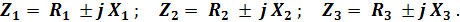
При этом ток в неразветвлённой части цепи равен произведению напряжения 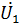на параллельном участке цепи на сумму комплексных проводимостей параллельно включённых сопротивлений

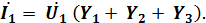
Сопротивления отдельных ветвей могут носить активно-реактивный характер при наличии индуктивных X_L и ёмкостных Х_С сопротивлений, поэтому в общем случае комплексные проводимости могут быть определены через активные q и реактивные bпроводимости:

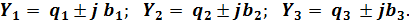
Модули полных проводимостей ветвей:

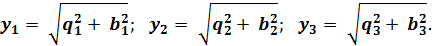
С учётом этого комплекс полной проводимости участка электрической цепи с параллельным соединением сопротивлений:

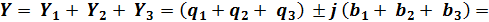
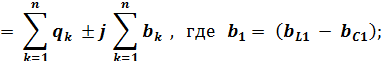
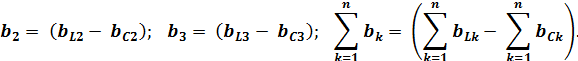
При этом активные и реактивные проводимости:

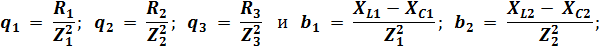
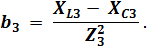
При смешанном соединении сопротивлений (см. рис. 2.1) электрическая цепь при расчёте приводится к виду рис. 2.2.

Полное сопротивление Z₁₂ участка цепи 1 – 2 может быть определено через её полную проводимость:

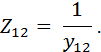При этом расчёт электрической цепи со смешанным соединением сопротивлений сводится к расчёту простейшей электрической цепи с последовательным соединением сопротивлений. Если при последовательном соединении сопротивлений векторная диаграмма строится, начиная с комплексного тока 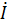, который является общим для всех сопротивлений, то при параллельном и смешанном соединении сопротивлений векторную диаграмму строят, начиная с вектора напряжения 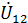на параллельном участке электрической цепи.

Литература. ГОСТ Р 52002 – 2003; [2] c. 67 − 87; [3] с. 66 – 93;

[4] с. 89 – 98, [5] с. 29 − 34.

Пример решения

Для последовательно − параллельной электрической цепи переменного тока (рис. 2.3, а,с. 21) определить токи I, I₁, I₂ на всех участках цепи, активную Р, реактивную Q и полную S мощности цепи. Построить векторную диаграмму напряжений и токов. Напряжение питания U = 127 В, активные и реактивные сопротивления цепи: R = 2 Ом; R₁ = 15 0м; R₂ = 10 Ом; X_L = 10 Ом, X_L₁ = 10 Ом; X_L₂ = 20 Ом; Х_С = 2 Ом; X_С1 = 20 Ом; Х_С2 = 30 Ом.

Решение. Полные сопротивления первой параллельной ветви

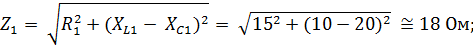
и второй параллельной ветви:

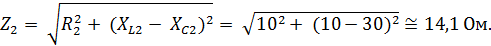
Активные проводимости первой и второй параллельных ветвей:

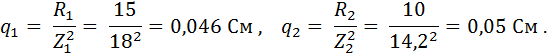
Суммарная активная проводимость параллельного участка цепи:

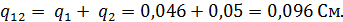
Реактивные проводимости первой и второй параллельных ветвей:

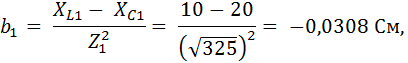
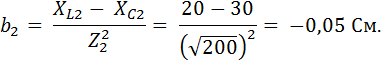
Общая реактивная проводимость параллельного участка цепи:

b₁₂ = b₁ + b₂ = − 0,0308 – 0,05 = − 0,081 См.

Полная проводимость параллельного участка цепи:

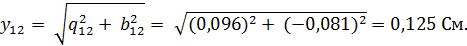
Полное сопротивление этого участка цепи:

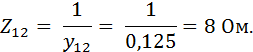
Активное и реактивное сопротивления параллельного участка цепи:

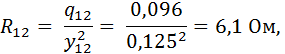
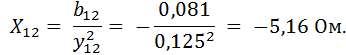
Активное и реактивное сопротивления всей цепи:

R_Ц = R + R₁₂ = 2 + 6,1 = 8,1 Ом,

Х_Ц = X_L + (−X₁₂) + (−X_C) = 10 – 5,16 – 2 = 2,84 Ом.

Полное сопротивление всей цепи:

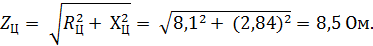
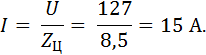Ток в неразветвленной части цепи:

Напряжения на отдельных участках цепи:

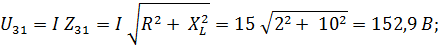
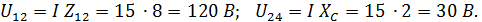
Токи в первой и во второй параллельных ветвях:

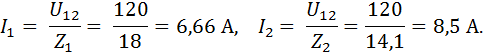
Коэффициенты мощности всей цепи:

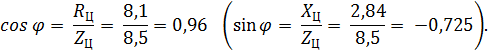
Коэффициент мощности участка 3 – 1 цепи:

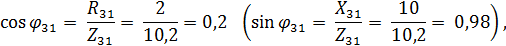
откуда .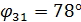

Коэффициент мощности участка 1 − 2 цепи:

для первого параллельного участка:

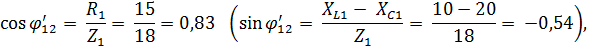
откуда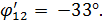

для второго параллельного участка:

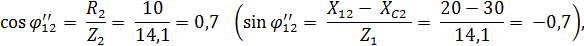
откуда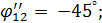

для всего участка 1− 2 цепи: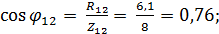

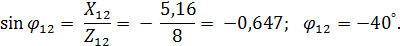
Коэффициент мощности участка 2 – 4 цепи: ,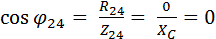

( ).

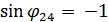Активная мощность отдельных участков цепи:

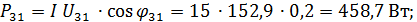
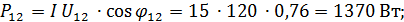
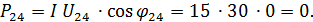
Суммарная активная мощность всей цепи:

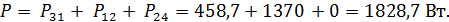
Реактивная мощность отдельных участков цепи:

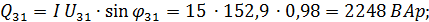
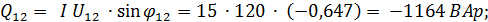
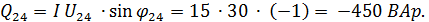
Суммарная реактивная мощность всей цепи:

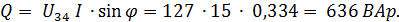
Векторная диаграмма для электрической цепи дана на рис. 2.3, б,с. 21.

Для построения векторной диаграммы составим уравнения по I и II законам Кирхгофа для схемы на рис. 2.3, а:

I з. К.: 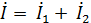(1)

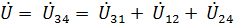II з. К.: (2)

Выбираем масштабы токов и напряжений. На комплексной плоскости строим горизонтально по действительной оси вектор напряжения 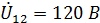на параллельном участке электрической цепи. Векторы токов 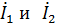опережают вектор 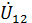на 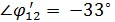, , 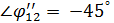т. к. в ветвях 1 – 2 преобладает активно-ёмкостной характер нагрузки. Согласно уравнению (1) общий ток 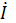равен векторной сумме токов 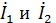и опережает вектор 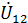на 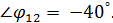Строим уравнение (2). Необходимо сложить три вектора напряжений 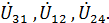К концу вектора 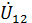под 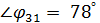к вектору тока 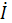строим в масштабе напряжений вектор 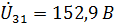(опережает , т. к. нагрузка в ветви 3 – 1 имеет активно-индуктивный характер). 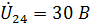Затем к концу вектора прибавляем вектор , перпендикулярный вектору тока 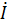(отстаёт от 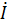, т. к. нагрузка в ветви 2 – 4 ёмкостная). Соединив начало координат с концом вектора 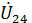получим вектор напряжения 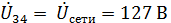согласно условию задачи. В результате вектор напряжения 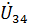опережает вектор тока 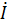, т. к. согласно расчёту вся сложная цепь имеет активно-индуктивный характер, т. е. задача решена верно.

123

Дата добавления: 2017-11-21; просмотров: 1779;