Квантово-механическая модель строения атома
В 1905 году А. Эйнштейн предсказал, что любое излучение представляет собой поток квантов энергии, называемых фотонами. Из теории Эйнштейна следует, что свет имеет двойственную (корпускулярно-волновую) природу.
В 1924 году Луи де Бройль (Франция) выдвинул предположение, что электрон также характеризуется корпускулярно-волновым дуализмом. Позднее это было подтверждено на опытах по дифракции электронов на кристаллах. Де Бройль предложил уравнение, связывающее длину волны λ электрона или любой другой частицы с ее массой m и скоростью ν:
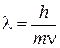 . .
| (3.6) |
Волны частиц материи Луи де Бройль назвал материальными волнами. Электрон имеет малую массу, следовательно, волновые свойства должны быть выражены ярко.
В 1927 году В. Гейзенберг (Германия) постулировал принцип неопределенности, согласно которому положение и импульс движения субатомной частицы (микрочастицы) принципиально невозможно определить в любой момент времени с абсолютной точностью. В каждый момент времени можно определить только лишь одно из этих свойств.
Таким образом, представление об атоме с определенными орбитами заменяется представлением о вероятностных положениях электронов в той или иной части атома.
Э. Шредингер (Австрия) в 1926 году вывел математическое описание поведения электрона в атоме:
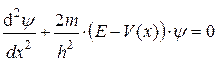
| (3.7) |
где m – масса электрона,
Е – полная энергия электрона в атоме,
V(x) – потенциальная энергия взаимодействия электрона и ядра,
ψ – волновая функция.
Распределение вероятности нахождения частицы в данный момент времени в некоторой области пространства будем описывать волновой функцией 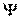 (x, y, z ,t) (пси-функция). Вероятность dP того, что частица находится в элементе объема dV, пропорциональная
(x, y, z ,t) (пси-функция). Вероятность dP того, что частица находится в элементе объема dV, пропорциональная 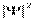 и элементу объемуdV:
и элементу объемуdV:
dP=  dV.
dV.
Физический смысл имеет не сама функция 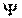 , а квадрат ее модуля – это плотность вероятности. Она определяет вероятность пребывания частицы в данной точке пространства.
, а квадрат ее модуля – это плотность вероятности. Она определяет вероятность пребывания частицы в данной точке пространства.
На базе перечисленных достижений квантовой механики была сформулирована квантово-механическая модель строения атома.
Вероятность нахождения электрона в определенной области пространства описывается волновой функцией ψ, которая характеризует амплитуду волны, как функцию координат электрона.
Волновые функции, которые удовлетворяют уравнению Шредингера, называются атомными орбиталями (АО), или по-другому, атомная орбиталь – это область пространства, в которых наиболее вероятно нахождение электрона.
Орбиталь в трехмерном пространстве ограничена поверхностями той или иной формы. Величина области пространства, которую занимает орбиталь, обычно такова, чтобы вероятность нахождения электрона внутри нее составляла не менее 95%.
Так как электрон несет отрицательный заряд, то его орбиталь представляет собой определенное распределение заряда, получившее название электронного облака.
Квантовые числа
Состояние электрона в атоме описывается при помощи четырех квантовых чисел.
Главное квантовое числоn определяет энергию и размеры электронных орбиталей. Главное квантовое число – номер энергетического уровня принимает значения 1, 2, 3, 4, 5, .... Чем больше номер уровня (n), тем выше энергия. Минимальной энергией обладает электрон, когда значение n = 1.
Энергетические уровни имеют буквенные обозначения: K (n = 1), L (n = 2), М (n = 3), N (n = 4), O (n = 5), P (n = 6), Q (n = 7). Переходы электронов с одного уровня на другой сопровождаются поглощением или выделением квантов энергии, которые могут проявиться в виде линий спектра.
Орбитальное квантовое число l. Детальное изучение спектров атомов показало, что линии спектров состоят из более тонких линий, т.е. электронные уровни расщеплены на подуровни. Орбитальное квантовое число характеризует энергию подуровня.
Орбитальные квантовые числа принимают целочисленные значения от 0 до (n – 1). Подуровни также обозначаются буквами:
| Подуровень: | s | р | d | f |
| Орбитальное квантовое число l: |
Орбитальное квантовое число определяет форму атомной орбитали (рис 3.3).
Электроны с орбитальным квантовым числом 0, называются s-электронами. Их орбитали и, соответственно, электронные облака имеют сферическую форму. Электроны с орбитальным квантовым числом 1 называются р-электронами. Форма их орбитали и, соответственно, электронных облаков напоминает гантель. Электроны с орбитальным квантовым числом 2 называют d-электронами. Орбитали имеют форму объемных четырех лепестков и «гантели с воротничком». Наконец, электроны с орбитальным квантовым числом 3 получили название f-электронов. Форма их орбиталей еще сложнее, чем форма d-орбиталей.
В одном и том же энергетическом уровне энергия энергетических подуровней возрастает (рис. 3.4): Еs < Ер < Еd < Ef.
В первом энергетическом уровне один (s-), во втором – два (s-, р-), в третьем – три (s-, р-, d-), в четвертом – четыре (s-, р-, d-, f-) подуровня
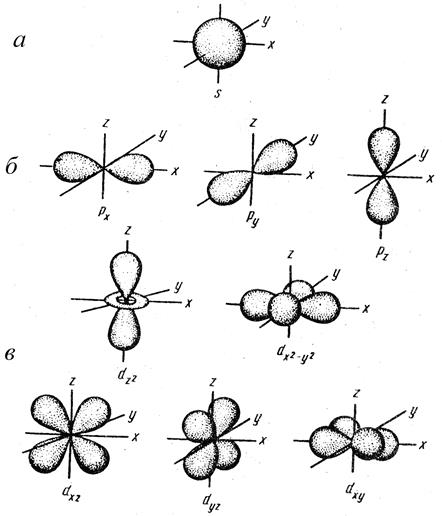
Рис. 3.3. Формы электронных облаков различных атомных орбиталей:
а – s; б – р; в – d.
Магнитное квантовое число – ml характеризует ориентацию орбиталей в пространстве. Орбитали несут отрицательный заряд, что обусловливает их взаимное отталкивание, вследствие чего орбитали имеют определенное направление в пространстве. Обладая магнитными свойствами, обусловленными движением электронов, орбитали, подобно магнитной стрелке, взаимодействуют с магнитным полем. Энергия взаимодействия разнонаправленных в пространстве орбиталей с силовыми линиями магнитного поля различна. Под воздействием внешнего магнитного поля происходит расщепление подуровней по энергии и, соответственно, расщепление линий спектра, которое было обнаружено в эксперименте.
Магнитное квантовое число принимает целочисленные значения от –l до +l, включая ноль. Соответственно, s-подуровень (l = 0) имеет одну орбиталь (ml = 0), р-подуровень (l = 1) – три орбитали (ml = –1, 0, +1), d-подуровень (l = 2) пять орбиталей (ml = –2, –1, 0, +1, +2), f-подуровень 7 орбиталей (ml = –3, –2, –1, 0, +1, +2, +3). Условно атомную орбиталь обозначают в виде клеточки.
Таблица 3.1
Значения магнитного квантового числа для орбиталей s-, p-, d-подуровней
| f | –3 | –2 | –1 | ||||
| d | –2 | –1 | |||||
| p | –1 | ||||||
| s |
Состояние электрона в атоме, характеризующееся конкретными n, m, l – то есть энергией, определенным размером, формой и ориентацией электронного облака в пространстве, называют атомной электронной орбиталью ( ). Общее число АО на уровнях равно n2.
Спиновое квантовое число ms. Изучение атомных спектров показало, что трех квантовых чисел недостаточно для описания свойств электронов. Каждый электрон также характеризуется собственным механическим моментом движения – спином.
Спиновое квантовое число ms имеет только два значения +½ и –½. Положительные и отрицательные значения спина связаны с направлением движения электрона. Два электрона с одинаковыми значениями n, m, l, но с противоположным направлением спинами, называется спаренными или неподеленной парой электронов. Электроны с разными спинами обычно обозначаются противоположно направленными стрелками ↑↓. Подобно двум электрическим катушкам, по которым электрический ток течет в противоположных направлениях, разнонаправленные электроны притягиваются друг к другу, что делает возможным их сосуществование в рамках одной орбитали.
Дата добавления: 2017-11-21; просмотров: 1425;











