ВИВЧЕННЯ РЕЗОНАНСУ В ЕЛЕКТРИЧНОМУ КОЛИВАЛЬНОМУ КОНТУРІ

Електричний коливальний контур складається з ємності С (конденсатора) та індуктивності L . В механізмі коливань в такому контурі можна виділити такі основні етапи.

1. Конденсатор заряджений, струм відсутній (рис.55.1). Вся енергія контуру зосереджена в електричному полі конденсатора - формула (55.1), де U_max - максимальне (амплітудне) значення напруги між обкладинками конденсатора.

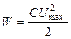(55.1)

2. Миттєвій розрядці конденсатора протидіє електрорушійна сила (ЕРС) самоіндукції. Коли струм досягне максимального (амплітудного) значення I_max(рис.55.2), конденсатор буде повністю розряджений і вся енергія контура буде рівна енергії магнітного поля індуктивності L з струмом I_max - формула (55.2).

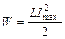(55.2)

3. Після того, як струм досягне максимального значення, ЕРС самоіндукції протидіє його зменшенню i ця ЕРС підтримує струм в тому ж напрямі, який i перезаряджає обкладинки конденсатора (рис.55.3), після чого процес розрядки конденсатора починається в зворотньому порядку. Таким чином, в електричному коливальному контурі відбуваються періодичні перетворення енергії електричного поля в енергію магнітного поля і навпаки. Такі перетворення без зовнішньої дії називаються вільними електромагнітними коливаннями. Згідно другого закону Кірхгофа для даного контуру має місце рівняння:

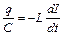, (55.3)

де 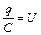- напруга між обкладинками конденсатора при миттєвому значенні заряду q, а весь вираз - ЕРС самоіндукції, яка діє в контурі. Враховуючи, що миттєве значення сили струму дорівнює (55.4), то рівняння (55.3) прийме вигляд (55.5).

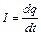, (55.4)

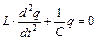, (55.5)

Розв'язком такого диференціального рівняння є гармонічна функція (55.6), де w₀ - циклічна частота коливань буде рівною (55.7),

q=q_maxsin(w₀t+j), (55.6)

(55.7)

Так, як 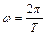, то з (55.7) отримаємо значення періоду власних незатухаючих коливань в електричному коливальному контурі:

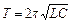. (55.8)

Що стосується максимального (амплітудного) значення заряду q_maxконденсатора і j₀ (початкової фази), то ці величини в рівнянні (55.6) визначаються тільки з початкових умов.

2. ВІЛЬНІ ЗАТУХАЮЧІ КОЛИВАННЯ В КОНТУРІ

Вільні незатухаючі коливання є ідеальним випадком. В реальних коливальних контурах завжди присутній активний опір, що приводить до затухання коливань, частина енергії контуру перетворюється у внутрішню енергію провідників (провідники нагріваються).

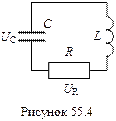На рис.55.4 наведена схема електричного коливального контуру, в якому резистор R характеризує активний опір всіх ділянок даного контуру. При силі струму I напруга U_R на кінцях резистора буде рівна (55.9) i тоді другий закон Кірхгофа прийме вигляд (55.10) (в лівій частині - сума напруг, в правій сума - ЕРС.)

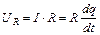(55.9)

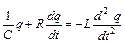(55.10)

Розв'язком рівняння (55.10) є функція (55.11),

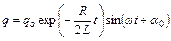, (55.11)

де q₀- заряд конденсатора в момент часу t=0, а частота коливань w в даному контурі визначається співвідношенням (55.12).

, (55.12)

Так, як миттєве значення струму знаходиться як перша похідна від заряду за часом (55.4), то взявши таку похідну, отримаємо:

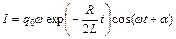, (55.13)

де добуток q₀w являє собою aмплiтyдне значення сили струму I₀ в момент часу t=0. Тому з рівняння (55.13) випливає, що в коливальному контурі з активним опором амплітуда коливань струму зменшується з часом за законом експоненти, а величину 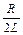позначають через b i називають коефіцієнтом затухання i тому рівняння (55.13)записують у вигляді (55.14).

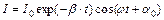, (55.14)

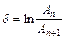(55.15)

На рис.55.5 наведений графік затухаючих коливань. Для характеристики самого затухання коливань вводять особливу величину (55.15), яку називають логарифмічним декрементом затухання: як логарифм відношення двох послідовних амплітудних значень сили струму (або амплітудних значень заряду чи напруги). Тут логарифм дуже зручна функція. Дійсно, якщо немає затухань, то А_n = А_n+1 i d = ln1 = 0, "нуль" вказує на відсутність затухань коливань.

3. ВИМУШЕНІ КОЛИВАННЯ В КОНТУРІ. ЯВИЩЕ РЕЗОНАНСУ

Якщо в електричному коливальному контурі буде діяти зовнішня змінна напруга, то в контурі під дією цієї напруги встановлюється вимушені коливання. На рис.55.6 джерело зовнішньої змінної напруги вказано символом (генератор).

Нехай зовнішня напруга U змінюється з часом за законом

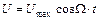, (55.16)

де U_max - амплітудне (максимальне) значення напруги, W - циклічна частота даної напруги (частота генератора). Тоді другий закон Кірхгофа для даного контуру прийме вигляд (55.17), тобто до лівої частини рівняння (55.10) ще додається зовнішня змінна напруга U.

Розв'язавши таке неоднорідне диференційне рівняння, отримаємо, що вимушені коливання в електричному коливальному контурі будуть відбуватись з частотою W, а амплітудне значення сили струму вимушених коливань буде рівним (55.18)

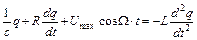(55.17).

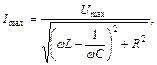(55.18)

Отримана залежність (55.18) аналогічна закону Ома, де роль опору грає величина (55.19), яка називається повним опором електричного кола змінного струму або імпедансом. Повний опір складається з активного (омічного) опору R ,індуктивного опору R_L=wL та ємнісного опору .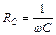

При R_L = R_C сила струму в контурі досягає максимального значення. Можна довести, що ця рівність виконується за умови: частота зовнішньої напруги Wспівпадає з частотою w₀ власних коливань контуру.

Явище різкого зростання амплітуди сили струму в коливальному контурі при наближенні частоти Wвимушуючої напруги до частоти w₀ власних коливань контуру називається явищем резонансу в електричному колі (коливальному контурі).

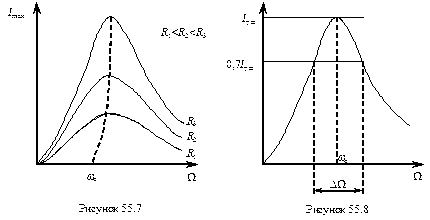На рис. 55.7 наведені залежності амплітудного значення сили струму в контурі від частоти зовнішньої (вимушуючої) напруги при різних значеннях активного опору контуру. Такі залежності називаються резонансними кривими. 3 зменшенням активного опору резонансні криві стають все більш "гострішими". Для визначення гостроти резонансної кривої задають однакове для всіх кривих зменшення сили струму 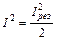або I = 0,7×I_рез . Чим гостріша резонансна крива, тим менший інтервал частот DWбіля резонансної частоти w₀, на кінцях якого виконується задана умова I = 0,7×I_рез (рис.55.8).

Відношення 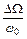характеризує відносну ширину резонансної кривої, а величина Q (55.20), обернена відносній ширині резонансної кривої називається добротністю контуру. Як показують окремі розрахунки, добротність контуру визначається через його електричні параметри співвідношенням (55.21).

, (55.20)

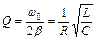, (55.21)

Можна довести, що добротність контуру дорівнює помноженому на 2p відношенню повної енергії електромагнітних коливань у контурі до енергії, яка витрачається на тепло Ленца-Джоуля за час одного повного коливання.