Сформулируем вторую задачу динамики для несвободной точки.

В случае несвободной материальной точки, во второй основной задаче динамики, требуется по заданным массе, активной силе, начальному положению и начальной скорости точки определить движение точки и реакцию связей .

Какая задача более сложная для свободной, или не свободной?

Эта задача для несвободной материальной точки принципиально отличается от подобной задачи для свободной материальной точки.

При решении второй основной задачи динамики для свободной точки главное правильно составить дифференциальные уравнения движения, после чего их всегда можно проинтегрировать точно или приближёнными способами, известными из теории дифференциальных уравнений.

Для несвободной точки, мы не можем приступить непосредственно к интегрированию ДУ.

Дело в том, что в эти уравнения входят шесть неизвестных: три координаты x, y, z точки и три проекции N_x, N_y, N_z силы реакции 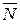, которая зависит не только от вида связи и активной силы 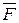, но и от самого движения точки. Поэтому прежде всего нужно каким бы то ни было способом исключить эту реакцию и только после этого можно приступить к интегрированию дифференциальных уравнений, уже не содержащих неизвестную реакцию, а затем по найденным уравнениям движения

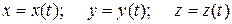
можно легко найти N_x, N_y, N_z

РС

При решении задач все силы можно разделить на силы зависящие от положения, скорости и времени.

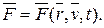
Примерами сил, зависящих от положения точки, являются упругая сила пружины, силы всемирного тяготения, кулоновы силы взаимодействия между зарядами.

К силам, зависящим от скорости, относятся силы сопротивления различных сред.

Сила, вызывающая колебания неуравновешенного мотора на упругом основании, служит примером силы, являющейся периодической функцией времени. К этому же классу сил относятся гидродинамические силы, действующие на винт корабля.