Векторный способ задания движения точки(дополнительно)
Пусть дано:
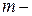 масса точки;
масса точки;
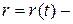 уравнение движения точки в векторной форме.
уравнение движения точки в векторной форме.
Определить 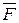 .
.
По заданному уравнению движения дифференцированием по времени находим вектор ускорения точки:
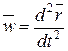
и, подставляя его в уравнение (1.6),определяем искомую силу
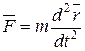 .
.
Координатный способ задания движения точки(обязательно)
Пусть дано:
m – масса точки;
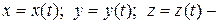 уравнения движения точки.
уравнения движения точки.
Определить: модуль и направление силы 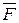 .
.
Дифференцируя дважды по времени уравнения движения, находим проекции ускорения точки на координатные оси
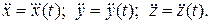
Затем воспользуемся уравнениями (1.8), из которых определяем проекции искомой силы
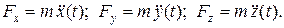
Эти проекции вполне определяют силу как величину векторную. Действительно, модуль силы равен
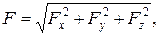
а её направление характеризуется выражениями
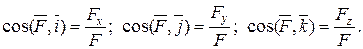
Адача
Материальная точка массой m движется согласно уравнениям
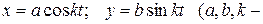 постоянные).
постоянные).
Определить силу, вызывающую заданное движение точки. (модуль и направление)
Решение.
Воспользуемся следующими уравнениями:
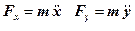
Определим вид траектории.
В кинематике мы рассматривали подобную задачу? Да.
Траекторией точки является эллипс

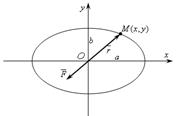
 |
Находим проекции ускореий на координатные оси.
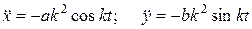 ,
,
т.к
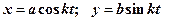
то данные уравнеия можно записать в другом виде
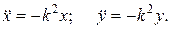
Отличие уравнений состоит в том, что в превом случае мы видим в чему равны производные в любой момент времени, а во втором случае в любом положении точки.
Следовательно проекции силы на оси координат будут равны:
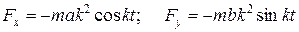 ,
,
или
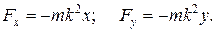
Откуда
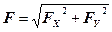
таким образом
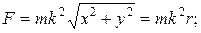
где

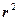 - модуль радиуса вектора.
- модуль радиуса вектора.
Сила действующая на точку , 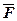 – переменная, пропорциональная первой степени растояния до точки О начала координат.
– переменная, пропорциональная первой степени растояния до точки О начала координат.
Определим как она направленна.
Силу 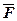 предстовляем в виде:
предстовляем в виде:
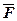 = FX
= FX 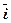 + FУ
+ FУ 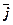
Подставляем
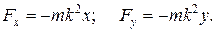 в данную формулу и получаем
в данную формулу и получаем
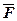 = - mk2(x
= - mk2(x 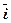 + у
+ у 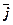 )
)
так как
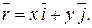
Итак
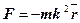
Чем отличается вектор силы от радиуса вектора?
Знаком и скаляром.
Сила 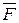 в любом положении точки на эллипсе направлена в противоположную сторону вектора
в любом положении точки на эллипсе направлена в противоположную сторону вектора 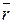 , то есть
, то есть 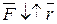
Таким образом, действующая на точку сила пропорциональна расстоянию точки от центра O , и её линия действия в любой момент движения проходит через неподвижный центр O.
Дата добавления: 2017-11-21; просмотров: 1348;











