Естественный способ задания движения точки (дополнительно)

Пусть дано:

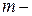масса точки;

траектория точки (следовательно, и её радиус кривизны );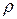

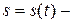уравнение движения точки в естественной форме (закон движения по траектории).

Определить: модуль и направление силы .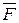

По уравнению движения точки вычисляем скорость, касательное и нормальное ускорения точки:

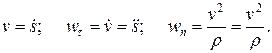
Далее из уравнения (1.10) находим проекции силы на естественные оси координат

Наконец,

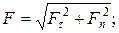
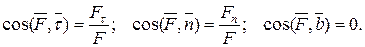
Итак, первая основная задача динамики свободной точки решается весьма просто при помощи операции дифференцирования.

Несмотря на свою простоту, эта задача сыграла важную роль в науке.

Опираясь на три эмпирических закона Кеплера (1571 ― 1630) ― немецкий математик и астроном, кинематически определяющих движение планет вокруг Солнца, Ньютон исследовал вопрос о том, какие силы действуют на планеты.

В результате решения этой первой задачи динамики Ньютон пришёл к открытию закона всемирного тяготения.

Первая задача динамики несовободной точки:

В случае несвободной точки в первой задаче динамики необходимо по заданной массе, активной силе, определить реакцию связей