Параметрические гипотезы.

В тех случаях, когда известен закон, но неизвестны значения его параметров (дисперсия или математическое ожидание) в конкретной ситуации, статистическую гипотезу называют параметрической.

Например, предположение об ожидаемом среднем доходе по акциям или разбросе дохода являются параметрическими гипотезами.

Большинство параметрических методов разработаны для нормально распределенных совокупностей. Некоторые методы позволяют анализировать данные, распределенные по другим законам (например, биномиальному или Пуассона).

Когда закон распределения генеральной совокупности не известен, но есть основания предположить, каков его конкретный вид, выдвигаемые гипотезы о виде его распределения называются непараметрическими.

Например, можно выдвинуть гипотезу, что число дневных продаж в магазине или доход населения подчинены нормальному закону распределения.

Непараметрические методы позволяют исследовать данные без допущений о характере распределения переменных. Так как в этих тестах обрабатывается не само измеренное значение, а его ранг, то эти тесты нечувствительны к выбросам. Непараметрические тесты могут применяться в тех случаях, когда переменные измерены при помощи порядковой или метрической шкалы. Существуют тесты, предназначенные для анализа номинальных данных.

Непараметрические методы наиболее приемлемы, когда объем выборок мал. Если данных много (например, n > 100), то не имеет смысла использовать непараметрические статистики. Когда выборки становятся очень большими, то выборочные средние подчиняются нормальному закону, даже если исходная переменная не является нормальной или измерена с погрешностью.

Таким образом, параметрические методы, являющиеся более чувствительными (имеют большую статистическую мощность), практически всегда подходят для больших выборок.

Предположение, которое касается неизвестного значения параметра распределения, входящего в некоторое параметрическое семейство распределений, называется параметрической гипотезой (напомним, что параметр может быть и многомерным). Предположение, при котором вид распределения неизвестен (т.е. не предполагается, что оно входит в некоторое параметрическое семейство распределений), называется непараметрической гипотезой. Таким образом, если распределение F(x) результатов наблюдений в выборке согласно принятой вероятностной модели входит в некоторое параметрическое семейство {F(x; θ), θ 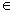Θ}, т.е. F(x) = F(x;θ₀) при некотором θ₀ 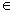Θ, то рассматриваемая гипотеза – параметрическая, в противном случае – непараметрическая.

Если и H₀ и H₁ – параметрические гипотезы, то задача проверки статистической гипотезы – параметрическая. Если хотя бы одна из гипотез H₀ и H₁ – непараметрическая, то задача проверки статистической гипотезы – непараметрическая. Другими словами, если вероятностная модель ситуации – параметрическая, т.е. полностью описывается в терминах того или иного параметрического семейства распределений вероятностей, то и задача проверки статистической гипотезы – параметрическая.