Представление ограничений ресурсов, капиталовложений и т.д. в виде линейных неравенств.

Первое упоминание (1938 г.) о математических методах в эффективном управлении производством принадлежит советскому математику Л. В. Канторовичу. Год спустя, в 1939 г., Л. В. Канторович опубликовал работу «Математические методы организации и планирования производства» и практически применил полученные результаты.

Термин «линейное программирование» ввели американские математики Дж. Данциг и Т. Купманс в конце 40-х годов. Дж. Данциг разработал математический аппарат симплексного метода решения задач линейного программирования (1951 г.). Симплексный метод находит применение для решения широкого круга задач линейного программирования и до настоящего времени является одним из основных методов.

Линейное программирование — это раздел математики, ориентированный на нахождение экстремума (максимума или минимума) в задачах, которые описываются линейными уравнениями. Причем линейными уравнениями описывается как сама целевая функция, так и входные параметры (переменные) условия ограничений на входные параметры.

Необходимым условием задач линейного программирования является обязательное наличие ограничений на ресурсы (сырье, материалы, финансы, спрос произведенной продукции и т.д.).

Другим важным условием решения задачи является выбор критерия останова алгоритма (проблема остановки (или проблема останова) - это одна из центральных проблем в теории алгоритмов, которая может неформально быть поставлена в виде: даны описание процедуры и её начальные входные данные, требуется определить, завершится ли когда-либо выполнение процедуры с этими данными. Альтернативой этому является то, что она работает всё время без остановки. Проблема остановки занимает центральное место в теории вычислимости, поскольку представляет собой первый пример задачи, которую невозможно решить алгоритмическим путём. Для многих других задач можно доказать их алгоритмическую неразрешимость, попытавшись свести задачу к проблеме остановки. Это делается по следующей схеме: пусть есть некая задача, для которой требуется установить её неразрешимость), т.е. целевая функция должна быть оптимальна в некотором смысле. Оптимальность целевой функции должна быть выражена количественно. Если целевая функция представлена одним или двумя уравнениями, то на практике такие задачи решаются достаточно легко.

Критерий останова алгоритма (или критерий оптимальности) должен удовлетворять следующим требованиям:

1. быть единственным для данной задачи;
2. измеряться в единицах количества;
3. линейно зависеть от входных параметров.

Исходя из вышесказанного, можно сформулировать задачу линейного программирования в общем виде:

• найти экстремум целевой функции

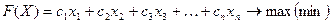
· при ограничениях в виде равенств:

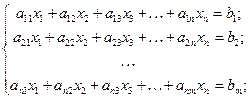
· при ограничениях в виде неравенств:

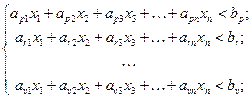
· и условиях неотрицательности входных параметров:

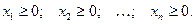
В краткой форме задача линейного программирования может быть записана так:

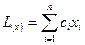
при условии

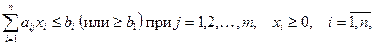
где 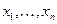- входные переменные;

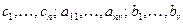- числа положительные, отрицательные и равные нулю.

В матричной форме эта задача может быть записана так:

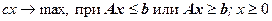
Задачи линейного программирования можно решить аналитически и графически.