Схема применения критерия

1. Выдвижение начальной гипотезы 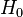, состоящей в том, что случайная величина X распределена по нормальному закону распределения.

2. Необходимо сравнить эмпирические (найденные экспериментальным путем) и теоретические (найденные исходя из закона распределения) частот. Однако как бы точно не был подобран закон распределения между теоретическими и эмпирическими частотами неизбежны расхождения возникает вопрос, объяснимы ли эти расхождения только случайными факторами, связанные с ограниченным числом наблюдений, или это связано с неправильным выбором теоретического закона распределения. Критерий Пирсона позволяет ответить на этот вопрос, однако как и любой другой критерий, он не доказывает справедливости гипотез, а лишь устанавливает ее согласие или несогласие с экспериментальными данными на принятом уровне значимости. 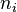В качестве проверки нулевой гипотезы применяется случайная величина χ², которая вычисляется по формуле где - эмпирические частоты, 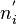- теоретические частоты.

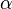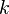3. По таблице χ²-Пирсона находят критические значения χ², которое зависит от двух параметров и , где 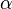- заданный уровень значимости (обычно 0,05 0,01 0,1) (то есть с вероятностью 0,95 0,99 0,9 можно гарантировать принятие или опровержение гипотезы) 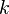- число степеней свободы. Оно находится по формул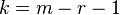е , где 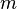- число групп (интервалов в вариационном ряду), - число параметров распределения (для нормального распределения , для показательного распределения 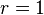, для равномерного )

4. Необходимо сравнить χ² критическое и χ² наблюдаемое. Если χ² критическое больше χ² наблюдаемого, то гипотеза принимается, если χ² критическое меньше χ² наблюдаемого, то гипотеза опровергается.

5. Сделать вывод из пункта 1.