Непараметрические обнаружители
Обнаружение на фоне негауссовских помех – сложный и недостаточно разработанный раздел теории обнаружения. Обнаружители, не зависящие от вида распределения, уменьшают зависимость вероятности ложной тревоги от статического характера сигнала на входе обнаружителя. Такой обнаружитель должен быть полезным в более широком кругу реальных ситуаций, чем параметрический обнаружитель. Для реализации непараметрических обнаружителей необходим переход к знаковым и ранговым алгоритмам.
В основе построения знаковых алгоритмов лежит нелинейное преобразование выборочного вектора 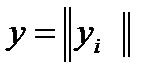 в знаковый sgn y
в знаковый sgn y
с элементами +1 при yi ≥ 0 и –1 при yi<0. В основе построения ранговых алгоритмов лежит нелинейное преобразованное выборочного вектора y в ранговый
rang y = 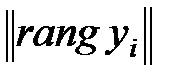
Ранги rang yi – это номера элементов yi вектора y, присваиваемые в порядке их возрастания (после «выстраивания по ранжиру»). Для выборочного вектора 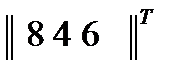 ранговым является вектор
ранговым является вектор 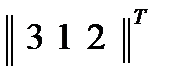 , т.е. наименьший ранг 1 имеет элемент 4, наибольший ранг 3 – элемент 8. Поскольку ранжирование учитывает наряду с фазовыми амплитудные соотношения, ранговый вектор несет большую информацию, чем знаковый той же размерности.
, т.е. наименьший ранг 1 имеет элемент 4, наибольший ранг 3 – элемент 8. Поскольку ранжирование учитывает наряду с фазовыми амплитудные соотношения, ранговый вектор несет большую информацию, чем знаковый той же размерности.
Знаковый и ранговый алгоритмы обнаружения сводятся к сопоставлению с порогом некоторой функции знакового (рангового) вектора, называемой знаковой (ранговой) статистикой. Для m-элементных сигналов с известными параметрами используют линейные статистики вида
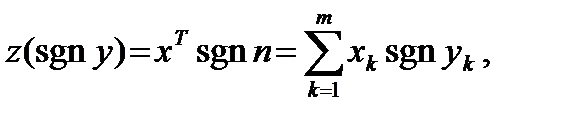 (4.17)
(4.17)
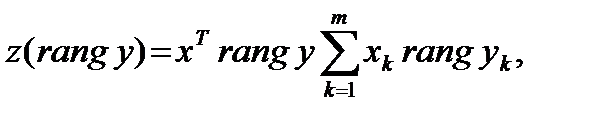 (4.18)
(4.18)
и нелинейные статики, в частности
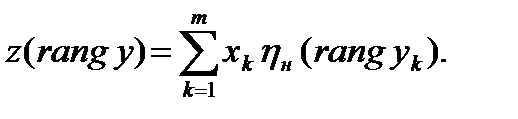 (4.19)
(4.19)
Функция ηн(u) – нелинейная, способная изменять динамический диапазон помеховых колебаний после ранговой обработки. Оказывается, что переход к рангам сжимает динамический диапазон дискрет стационарного гауссовского шума. Нелинейная ранговая статистика Ван-дер-Вардена предусматривает, поэтому расширение динамического диапазона перед корреляционной обработкой. Для этого функция ηн(u) берется обратной функции «интеграл вероятности».
Обнаружители, не зависящие от вида распределения, можно классифицировать несколькими способами. Эти обнаружители могут быть с фиксированными или последовательными объемами выборок и бинарными или многоальтернативными. Можно выделить следующие модели обнаружителей.
Модель 1. Соответствует случаям, когда совместная функция распределения входного сигнала обнаружителя при отсутствии сигнала известна, а совместная функция распределения смеси сигнала с шумом — неизвестна.
Модель 2. Соответствует случаям, когда обе выше названные функции распределения неизвестны, но имеется выборка данных, о которой известно, что она имеет распределение шума. Эта выборка называется выборкой чистого шума.
Модель 3. К ней относятся обнаружители с k-выборкой, когда неизвестны распределения, указанные в модели 1 и отсутствует выборка чистого шума. Эта модель характерна для радиолокационных обнаружителей, так как большинство обзорных РЛС обладают большим числом элементов разрешения по дальности, по допплеровской частоте и т.д.
Дата добавления: 2021-02-19; просмотров: 509;











