Главные направления, главные диаметры

О п р е д е л е н и е. Направление называется главным направлением относительно линии второго порядка, если оно сопряжено с перпендикулярным ему направлением.

Т е о р е м а. Относительно любой линии второго порядка, отличной от окружности, существуют два и только два главных направления. Относительно окружности любое направление является главным.

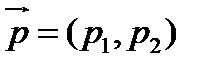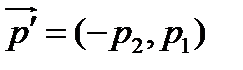Д о к а з а т е л ь с т в о. Записав условие сопряженности для ортогональных направлений и , получим условие

, ( )

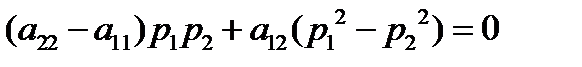которое позволяет найти главные направления и определить их число.

I. Пусть в ( ) 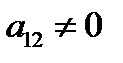. Тогда 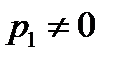(в противном случае получим 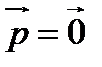). Из ( ) получаем квадратное уравнение с неизвестным 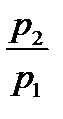. Это уравнение имеет два различных корня, так как дискриминант больше нуля. Следовательно, в этом случае относительно линии второго порядка существуют ровно два главных направления.

II. Если в ( ) 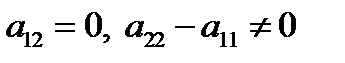, то получаем 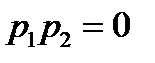. Имеем два главных направления 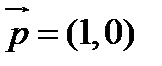и 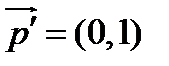– направления координатных осей.

III. Если в ( ) 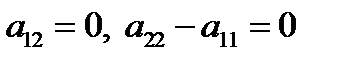, то есть ( ) является тождеством, то любое направление является главным относительно линии второго порядка. В этом случае уравнение линии приводится к каноническому уравнению 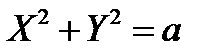. То есть линия является окружностью (вещественного, нулевого или мнимого радиуса).

О п р е д е л е н и е. Диаметр линии второго порядка называется главным диаметром, если он перпендикулярен сопряженным хордам.

Таким образом, главный диаметр является осью симметрии линии второго порядка.

Из следствия о диаметрах нецентральной линии следует, что нецентральная линия имеет только один главный диаметр – ось симметрии асимптотического направления.