ГЛАВНЫЕ ЗАКОНЫ МЕХАНОДИНАМИКИ

Прежде чем знакомиться с главными законами механодинамики, обратим внимание на то, что главный носитель информации и тепловой энергии – фотон движется в пространстве прямолинейно и равномерно со скоростью 300000км/с и нам надо иметь математическую модель, описывающую такое движение фотона. Но, первый закон динамики Ньютона, описывающий словесно равномерное и прямолинейное движение, не имеет математической модели и это сразу затрудняет анализ поведения фотона в различных процессах и явлениях.

Так как фотон имеет массу, то согласно первому закону динамики Ньютона сумма сил, действующих на него, равна нулю и мы лишаемся возможности описать прямолинейное и равномерное движение фотона и найти силы, движущие его с постоянной скоростью, близкой к 300000км/сек. Это явный и яркий пример нарушения принципа причинности. Следствие – равномерное прямолинейное движение фотона - известный факт, а причина, реализующая это движение, отсутствует. Почему?

Ошибка, сформировавшая такое представление, оказалась простой. Равномерное прямолинейное движение любого тела и любого материального объекта, в том числе и фотона, всегда следует после ускоренного движения, поэтому закон, описывающий равномерное движение любых материальных объектов нельзя ставить на первое место. Равномерное движение материальных объектов всегда- следствие ускоренного движения. Поставка на первое место следствия затрудняет определение причины рождения этого следствия. Вроде бы просто, но человечеству потребовалось более 300 лет, чтобы увидеть и понять эту простоту, в которой скрывалось нарушение причинно-следственных связей.

Исправление описанной ошибки, привело к пересмотру законов динамики Ньютона, которая получила уже более точное название – Механодинамика. Так как обитатели микромира имеют массы, электрические и магнитные поля, то невозможно описание их поведения и взаимодействий без знаний новых законов механодинамики.

Учитывая, что учебная информация в существующих школьных и вузовских учебниках по физике и химии находится сейчас в полностью разрушенном состоянии, непригодном для образования, мы приведём здесь лишь начальные основы механодинамики, так как без них невозможно понимание ряда разделов физхимии микромира.

Обратим внимание на главное ещё раз: все тела всегда начинают двигаться ускоренно. У нас нет ни единого примера, когда тело сразу начало бы двигаться равномерно. Теоретически это возможно, а в реальности этого нет. Поэтому у нас остаётся одна возможность - начинать изучение законов движения тел с фазы ускоренного движения. На рис. 2 закономерность равномерного изменения скорости тела при его ускоренном движении представлена линией ОА.

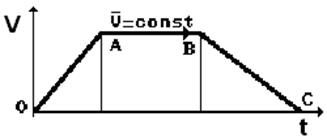
Рис. 2. График изменения скорости движения тела

И так, все тела всегда начинают свои движения с фазы увеличения скорости от нулевой величины. Эту фазу называют фазой ускоренного движения тела. Она является начальной фазой у всех тел и всегда. Значит, это - закон Природы и мы не имеем права игнорировать его. Мы не имеем права начинать изучение движения тела с любой последующей фазы, которая может быть фазой равномерного движения тела (АВ на рис. 2) или с фазы его замедленного движения (ВС на рис. 2). Почему мы не имеем научного права начать изучение тела с фазы его равномерного движения (АВ на рис. 2)? Да потому что мы обязаны знать кинематические и динамические характеристики тела, перешедшего с фазы ускоренного движения к фазе равномерного движения.

Равномерное движение тела является следствием ускоренного движения. Поэтому, начав изучать фазу равномерного движения тела, проигнорировав предшествующую этому фазу его ускоренного движения, мы теряем информацию о силах, которые действовали на тело в фазе его ускоренного движения. В результате первый закон динамики Ньютона не имеет математической модели сил, действующих на равномерно движущееся тело. Это главная научная причина, которая запрещает нам начинать изучение движения тела с фазы его равномерного движения. Но эту причину игнорировали все со времён Ньютона. К чему это привело? Покажем на конкретном примере. Поскольку все тела начинают свои движения с фазы ускоренного движения, то, взяв автомобиль в качестве модели такого тела, приложим к нему все силы, которые действуют на него в фазе ускоренного движения (рис. 3) [2].

Главная сила, движущая автомобиль ускоренно, - ньютоновская сила 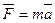. Далее, Даламбер установил, что на всякое ускоренно движущееся тело, действует сила инерции, направленная противоположно движению и равная произведению массы тела на его ускорение 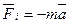. Но сила инерции не одна сопротивляется ускоренному движению автомобиля, а вместе с механическими и аэродинамическими силами, которые мы обозначаем символом 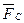. Согласно принципу Даламбера сумма сил, действующих на движущееся тело в каждый данный момент времени, равна нулю и мы имеем уравнение сил, действующих на ускоренно движущийся автомобиль

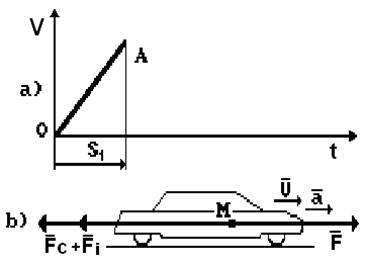
Рис. 3. Схема сил, действующих на автомобиль в фазе его ускоренного движения

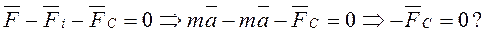(1)

Странный результат (1). Сумма сил механических и аэродинамических сопротивлений, действующих на ускоренно движущийся автомобиль, равна нулю. Почему? Почему не искали ответ на этот вопрос со времён Даламбера? Первое предположение побуждает нас поставить под сомнение правильность определения силы инерции. Действительно, если бы сила инерции не была равна 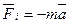, то и не было в формуле (1) столь абсурдного противоречия. Так как сила инерции сопротивляется ускоренному движению не одна, а вместе с силами механических и аэродинамических сопротивлений, то она в принципе не может быть равна массе 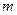тела умноженной на ускорение 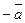. Возникает вопрос: на каком основании в определении силы инерции участвует ускорение? Ведь оно не ускоряет, а замедляет движение автомобиля, причём замедляет не одна, а вместе с силами механических и аэродинамических сопротивлений. Из этого следует, что в выражениях силы инерции и сил механических и аэродинамических сопротивлений должен быть показатель, который бы разделял между ними их общее замедляющее действие, которое должно быть равно ньютоновскому ускорению. Назовём этот показатель замедлением и обозначим, замедление, формируемое силой инерции, символом 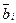, а замедление, формируемое силами механических и аэродинамических сопротивлений, символом 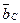и внесём эти изменения в рисунок (рис. 4).

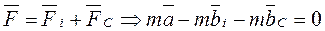. (2)

Из этого уравнения автоматически следует логическая связь между ньютоновским ускорением 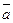и замедлениями 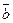, формируемыми силами сопротивления ускоренному движению автомобиля

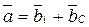. (3)

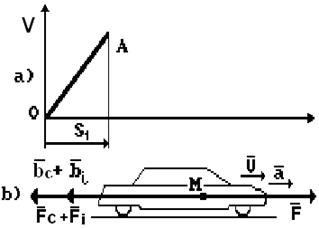
Рис. 4. Схема сил, действующих на ускоренно движущийся автомобиль,

а также - ускорений и замедлений, формируемых этими силами

Итак, сила инерции равна 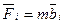. Замедление 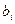, формируемое силой инерции, определится по формуле

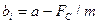. (4)

А теперь представим схему сил, действующих на автомобиль, перешедший с фазы ускоренного движения в фазу равномерного движения (рис. 5).

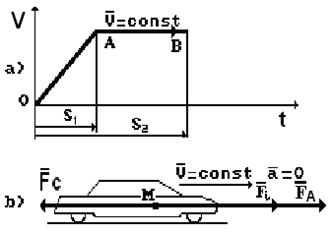
Рис. 5. Схема сил, действующих на равномерно движущийся автомобиль

(5)

Это математическая модель второго закона механодинамики, бывшего первого закона динамики Ньютона, не имевшего математической модели. Сила инерции , входящая в эту модель (5), определяется из математической модели (2) ускоренного движения автомобиля, а суммарная сила всех видов сопротивлений - экспериментальная сила, определяемая с помощью соответствующих экспериментальных коэффициентов сопротивления равномерному движению автомобиля.

Итак, ошибочная постановка на первое место ньютоновского закона равномерного движения тела приводит к тому, что в сумме сил, действующих на равномерно движущееся тело, теряется сила инерции, которая возникает при ускоренном движении тела и продолжает действовать на него после перехода к фазе равномерного движения, изменив при этом своё направление на противоположное.

Следующая ошибка связана с законом сохранения импульса, который широко используется при описании поведения обитателей микромира. Поясним её на примере галилеевского эксперимента (рис. 6).

а)	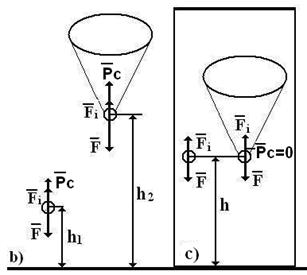b) современное представление эксперимента Галилея

Рис. 6. Схема эксперимента Галилея

Галилей разместил в трубке предметы разной массы и плотности, выкачал из неё воздух и показал, что все они опускаются под действием силы тяжести с одной и той же скоростью (рис. 6, а). Тогда как скорость их падения в открытом пространстве разная.

Удивительно то, что Исаак Ньютон и все его последователи, включая Даламбера, не поняли физическую суть этого эксперимента и его следствия. Для прояснения причины этого представим более наглядную схему этого эксперимента (рис. 6, b и с). Возьмём одно тело – металлический шарик. Представим его падение на Землю в двух вариантах: без парашюта и с парашютом, в свободном воздушном пространстве (рис. 6, b) и в изолированном пространстве с выкаченным воздухом (рис. 6, с). Приложим силы, которые действуют на шарик с парашютом и без него в воздушном пространстве и в пространстве с выкаченным воздухом.

Главная сила, действующая на шарик, - сила тяжести Земли 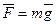. Эта сила эквивалентна силе второго закона Ньютона, поэтому назовём её ньютоновской силой. Так как шарик движется под действием силы тяжести с ускорением свободного падения 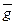, то на него действует сила инерции, которую Даламбер определил по формуле 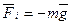и направил её противоположно направлению ускорения 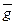. Но в открытом пространстве, кроме силы инерции, направленной противоположно его движению, действует и аэродинамическая сила 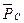(сила сопротивления воздуха), также направленная противоположно движению шарика (рис. 6, b). Вполне естественно, что на шарик с парашютом действует большая сила аэродинамического сопротивления 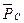, чем на шарик без парашюта. Согласно принципу Даламбера, в любой момент времени сумма сил, действующих на движущееся тело, равна нулю

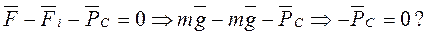(6)

Итак, мы не нарушили ни одного закона динамики Ньютона и ни одного правила составления уравнения сил, действующих на падающее тело, и получили абсурдный результат (6) – сопротивление воздуха, действующего на падающий шарик, равно нулю.

А теперь составим уравнение сил, действующих на шарик, когда он движется под действием силы тяжести в безвоздушной среде (рис. 6, с). Вполне естественно, что силы сопротивления воздуха не будет. Шарик с парашютом и без парашюта будут опускаться под действием одной и той же силы – силы тяжести (если массу парашюта не учитывать) и с одной и той же скоростью. Но сила инерции останется, так как величина силы тяжести по мере приближения шарика к Земле будет увеличиваться в соответствии с законом всемирного тяготения Ньютона

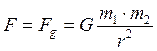. (7)

Уравнение сил, действующих на шарик, в этом случае запишется так

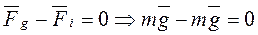. (8)

Но шарик ведь опускается. Почему? Потому что сила гравитации 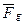- величина переменная. В данном случае она увеличивается в соответствии с законом всемирного тяготения (7)

По мере приближения шарика к Земле расстояние между ним и центром Земли уменьшается, а сила гравитации 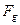растёт, поэтому будет точнее, если уравнение (7) записать так

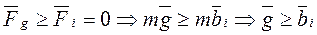. (9)

Как видно, символ ускорения свободного падения 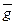в выражении даламберовской силы инерции 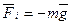мы заменили новым символом 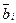( 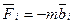). Поскольку сила инерции не ускоряет, а замедляет движение шарика, то она формирует замедление, которое мы обозначили символом 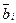. Это позволяет нам объяснить причину падения шарика (рис. 6, с). Он падает потому, что замедление 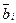, формируемое силой инерции, меньше ускорения 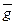свободного падения шарика. Обозначим замедление падению шарика в открытом пространстве, формируемое воздухом, символом 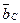. Тогда уравнение (6) запишется так

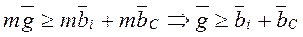. (10)

Представленный анализ эксперимента Галилея значительно проясняет его физическую суть, а новые законы механодинамики, как мы увидим ниже, значительно упрощают описание поведения обитателей микромира, особенно - фотона.

ФОТОН

Вводная часть

В ХХ веке считалось, что электромагнитное излучение формируется электромагнитными волнами Максвелла, состоящими из двух взаимно перпендикулярных синусоид, описывающих изменение напряжённостей электрического Е и магнитного Н полей (рис. 7). Однако, новые интернетовские процессы формирования, передачи и приёма информации поставили такую структуру излучения под сомнение, так как она не позволяла получать ответы на многие вопросы. Поэтому пришлось вернуться к идее индийского учёного Бозе, который предположил в 1924 году, что излучаемое электромагнитное поле представляет собой совокупность фотонов, которую он назвал идеальным фотонным газом.

Английский учёный Алан Холден представил совокупность фотонов, формирующих волну, в виде шариков (рис. 8). В результате возникла задача выявления внутренней структуры шариков, формирующих такую волну. Но эта задача оказалась достаточно сложной [1].

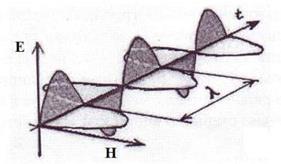
Рис. 7. Схема электромагнитной волны

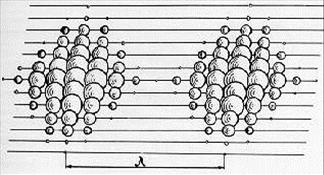
Рис. 8. Схема фотонной волны длиною

Тем не менее, она была решена российской наукой и мы проследим последовательность её решения. Необходимость знания этой последовательности обусловлена тем, что на ней базируется вся последующая информация о формировании и поведении обитателей микромира. Поэтому изучению теории фотона надо уделить особое внимание. Её математическое содержание многократно проще математических теорий электромагнитного излучения, господствовавших в ХХ веке. Однако, образное представление физической сути, содержащейся в математических символах новой теории фотона, сложнее.

В XX веке мало уделялось внимания пониманию физической сути излучений, поэтому сформировались условия, при которых математическое описание было поставлено на первое место. Мы же на первое место ставим формирование физических представлений о структурах и поведении обитателей микромира при их взаимодействиях, а математическое описание – на второе место.

Вполне естественно, что последовательность познания структуры фотона надо базировать на давно известных математических моделях, которые описывают его поведение в различных экспериментах. Поскольку фотонную волну (рис. 8) формируют корпускулы - фотоны, то теория, которая описывает их корпускулярные свойства, названа корпускулярной теорией фотона.