Центр линии второго порядка
Пусть относительно аффинной системы координат 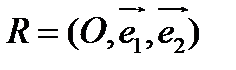 линия
линия 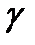 второго порядка задана уравнением
второго порядка задана уравнением
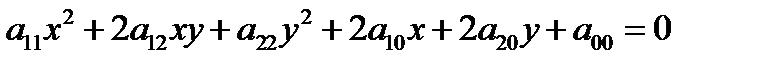 (1)
(1)
О п р е д е л е н и е. Центром линии второго порядка называется точка, координаты которой удовлетворяют системе
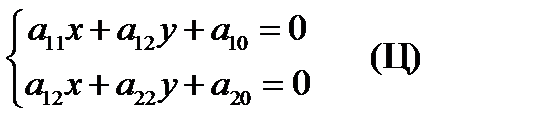
Число центров линии второго порядка зависит от определителя системы (Ц):
· Если 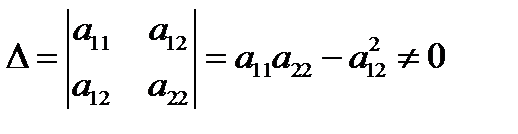 , то система (Ц) имеет единственное решение, то есть линия
, то система (Ц) имеет единственное решение, то есть линия 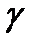 имеет единственный центр и называется центральной линией.
имеет единственный центр и называется центральной линией.
Можно проверить, что эллипс, мнимый эллипс, гипербола, пара пересекающихся прямых, пара мнимых пересекающихся прямых являются центральными линиями.
· Если 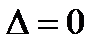 , то система (Ц) либо имеет бесконечно много решений, либо не имеет решений. Соответственно линия второго порядка либо имеет бесконечно много центров (пара параллельных прямых, пара мнимых параллельных прямых, пара совпавших прямых), либо не имеет центра (парабола).
, то система (Ц) либо имеет бесконечно много решений, либо не имеет решений. Соответственно линия второго порядка либо имеет бесконечно много центров (пара параллельных прямых, пара мнимых параллельных прямых, пара совпавших прямых), либо не имеет центра (парабола).
Перенеся начало репера 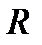 в точку
в точку 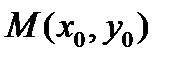 – центр линии
– центр линии 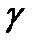 , получим уравнение этой линии в репере
, получим уравнение этой линии в репере 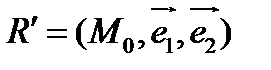 :
:
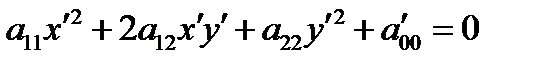 ,
,
из которого видно, что точка 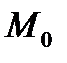 – центр линии второго порядка, является центром симметрии линии
– центр линии второго порядка, является центром симметрии линии 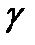 .
.
Дата добавления: 2021-09-25; просмотров: 567;











