Диаграммы состав - свойство для равновесия жидкость - пар
Для изучения сложных многокомпонентных систем в тех случаях, когда трудно установить точные аналитические зависимости между различными параметрами состояния и свойствами системы применяется метод физико-химического анализа.
Физико-химический анализ – это метод, который посредством геометрического исследования диаграмм фактор равновесия - свойство устанавливает число, химическую природу и границы существования фаз в равновесных системах образованных одним, двумя или несколькими компонентами. Основным приемом физико-химического анализа является построение диаграмм состояния в виде диаграмм состав – свойство. Состав на диаграммах обычно откладывают по оси абсцисс, а свойство по оси ординат.
Геометрический метод изучения превращений, происходящих в равновесных системах, основывается на двух основных положениях, сформулированных Курнаковым: принцип непрерывности и принцип соответствия.
Принцип непрерывностизаключается в том, что при непрерывном изменении параметров, определяющих состояние системы (давление, температура, концентрация), свойство ее отдельных фаз изменяются тоже непрерывно. При появлении новых или исчезновении существующих фаз свойства системы как целого изменяются скачком.
Принцип соответствиясостоит в том, что каждой фазе или комплексу фаз на диаграмме отвечает определенный геометрический образ (точка, линия, поверхность и т.п.).
Диаграммы давление насыщенного – состав, температура – состав, состав жидкости – состав пара для идеальных растворов могут быть рассчитаны с использованием законов Рауля и Дальтона. На практике используются в основном диаграммы температура – состав (диаграммы перегонки) для расчетов процессов разделения и очистки жидких смесей.
Диаграммы температура – состав (T – x) могут быть получены и экспериментально на основе измерений температуры кипения растворов и чистых компонентов и определения состава равновесного с кипящей жидкостью пара.
Диаграммы перегонки идеальных растворов имеют вид, подобный рисунку 2.3.
Рисунок 2.3 - Диаграмма температура кипения – состав при постоянном давлении
для идеального раствора
Точки a и b на рисунке 2.3 показывают температуры кипения чистых компонентов: a – температура кипения чистого компонента 1, b – температура кипения чистого компонента 2. Ниже кривой aceb лежит область устойчивого существования одной жидкой фазы, выше кривой adfb – область устойчивого существования пара. Между кривыми aceb и adfb наблюдается такое сочетание температур и составов, при котором неустойчивая однофазная система распадается на две термодинамически устойчивые фазы – взаимно насыщенные раствор и пар. Нижняя кривая aceb изображает зависимость температуры начала кипения от состава раствора и состав жидкой фазы в двухфазной системе жидкость – пар (точки c и e). Ее называют линией кипения или линией испарения. Верхняя кривая adfb показывает температуру конца кипения, т. е. температуру, при которой вся жидкость превратится в пар, и состав паровой фазы в двухфазной системе жидкость – пар (точки d и f). Эта же линия показывает температуру начала конденсации пара, если насыщенный пар охлаждать. Ее называют линией конденсации.
Из рисунка 2.3 видно, что пар по сравнению с жидкостью обогащен компонентом 2, температура кипения которого ниже. Таким образом, пар, находящийся в равновесии с жидкостью, обогащен тем компонентом, добавление которого приводит к понижению температуры кипения, т.е. более летучим компонентом. Это заключение носит название – первый закон Коновалова-Гиббса.
Анализируя диаграмму температура – кипения состав, можно определить, какие фазы находятся в равновесии в определенном диапазоне температур и составов, температуру начала и конца кипения раствора, температуру начала и конца конденсации пара, состав жидкости и состав пара при кипении и конденсации.
Для неидеальных растворов закон Рауля не выполняется. Возможны два вида отклонений от закона Рауля: положительные и отрицательные.
При положительных отклонениях от закона Рауля давление пара больше, чем над идеальными растворами. Примерами таких систем являются растворы кислород – азот, этанол – диэтиловый эфир, бензол – ацетон. Положительные отклонения приводят к тому, что температура кипения раствора понижается, так как при более низких температурах достигается равенство давления насыщенного пара и внешнего давления, что и приводит к кипению. При этом линия кипения на диаграмме T – x прогибается вниз.
При определенных соотношениях между разностью давлений пара чистых компонентов и степенью положительных отклонения от закона Рауля на диаграммах T – x возможно появление минимумов (рисунок 2.4а).
| | |
| Рисунок 2.4 – Диаграммы температура кипения – состав для неидеальных растворов с сильными положительными (а) и с сильными отрицательными отклонениями (б) от закона Рауля |
При отрицательных отклонениях от закона Рауля давление пара ниже, чем над идеальными растворами. Примерами таких систем являются растворы хлороформ – диэтиловый эфир, хлороформ – бензол, четыреххлористый углерод – диэтиловый эфир. Отрицательные отклонения приводят к тому, температура кипения раствора повышается, так как при более высоких температурах достигается равенство давления насыщенного пара и внешнего давления, соответствующее кипению. При этом линия кипения на диаграмме T – x прогибается вверх.
При определенных соотношениях между разностью давлений пара чистых компонентов и степенью отрицательных отклонения от закона Рауля на диаграммах T – x возможно появление максимумов (рисунок 2.4б).
Экстремумы на зависимостях температура кипения – состав (точки c на рисунке 2.4) называются азеотропными точками. В этих точках состав жидкости и пара одинаков.
Таким образом, по виду диаграммы температура кипения – состав можно определить идеальный раствор или нет и какие отклонения от закона Рауля для него характерны.
Пример: По диаграмме температура кипения – состав системы диэтиловый эфир – четыреххлористый углерод, представленной на рисунке 2.5 определим:
1. Идеальный ли раствор образуют эти вещества? Если нет, то, какие отклонения от закона Рауля характерны для этого раствора?
2. При какой температуре закипит жидкость, содержащая 70 % (мол.) (C2H5)2O.
3. При какой температуре вся первоначальная жидкость обратится в пар, если при нагревании пар не отводить?
4. Как будет меняться состав первоначальной жидкости по мере испарения?
5. Каков состав первых пузырьков пара?
6. Как изменяется состав равновесного с кипящей жидкостью пара в ходе испарения?
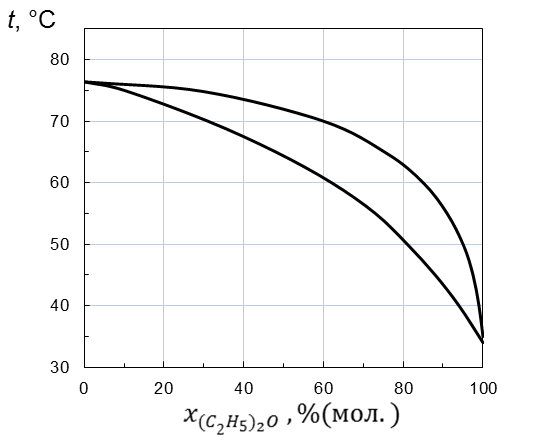
Рисунок 2.5– Диаграмма температура кипения – состав системы
(C2H5)2O – CCl4 при стандартном давлении
Решение:
1. Нижняя линия, показывающая зависимость температуры кипения раствора от состава прогибается вверх, т. е. температура кипения раствора выше, чем, если бы он был идеальным. Следовательно, раствор неидеальный с отрицательными отклонениями от закона Рауля.
2. По нижней линии находим, что жидкость, содержащая 70 % (мол.) (C2H5)2O закипит при температуре 56 ºС.
3. По верхней линии находим, что вся первоначальная жидкость, содержащая 70 % (мол.) (C2H5)2O превратится в пар, т. е. кипение закончится, при температуре 67 ºС.
4. По нижней линии находим, что последние капли жидкости при температуре конца кипения 67 ºС будут содержать 40 % (мол.) диэтилового эфира. Следовательно, состав первоначальной жидкости по мере испарения будет меняться от 70 до 40 % (мол.) (C2H5)2O.
5. По верхней линии при температуре начала кипения 56 ºС находим, что состав первых пузырьков пара 89 % (мол.) (C2H5)2O.
6. По верхней линии находим, что состав равновесного с кипящей жидкостью пара в ходе испарения меняется от 89 до 70% (мол.)(C2H5)2O.
Диаграммы температура кипения – состав дают возможность оценить не только составы соответствующих фаз, но и их относительные количества. Для этой цели используют, так называемое, правило рычага, которое можно записать в форме уравнения (см. рисунок 2.6):
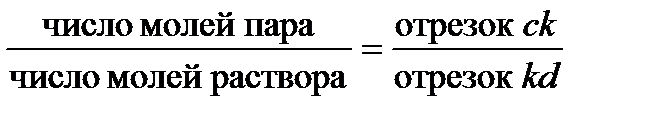
| (2.29) |
Если состав раствора выражен не молярными долями, а массовыми (или массовыми процентами), то и количества фаз следует выражать в единицах массы:
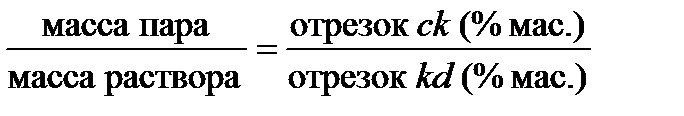
| (2.29а) |
Рисунок 2.6 – К выводу правила рычага
Чтобы найти абсолютные количества надо использовать еще одно соображение: при кипении общее количество веществ в системе остается постоянным, происходит лишь перераспределение веществ между фазами. Таким образом, чтобы определить массу жидкой и паровой фазы при любой температуре надо решить систему уравнений:
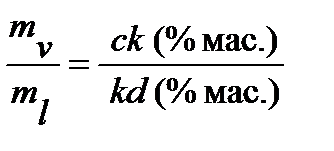
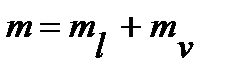
Использование правила рычага не ограничивается упомянутым соотношением количеств жидкости и пара. Оно применимо к любым двухфазным равновесным системам.
Пример: Какое количество каждого из компонентов смеси будет находиться в жидкой фазе и в паре, если 0,9 кг раствора (C2H5)2O – CCl4, содержащего 70 % (мол.) (C2H5)2O, нагреть до температуры 60 ºC?
Решение:
Количество жидкой и парообразной фазы находится по правилу рычага (рисунок 2.7):
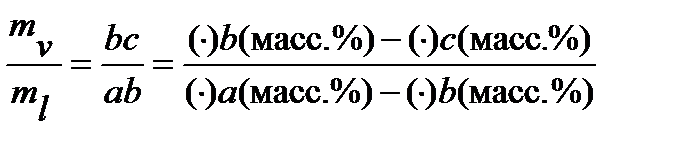
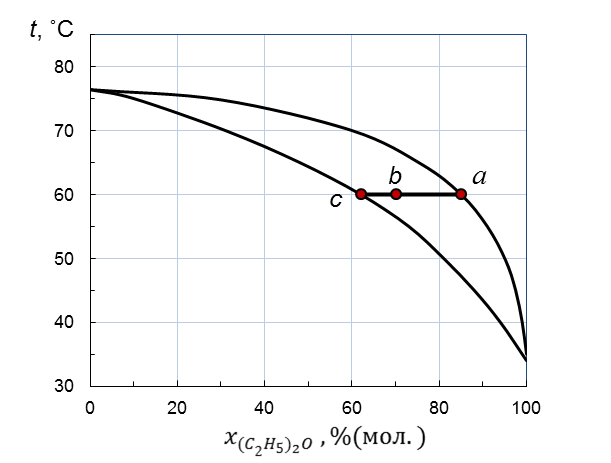
Рисунок 2.7 – Правило рычага для диаграммы температура кипения – состав
системы (C2H5)2O – CCl4 при стандартном давлении
Из рисунка 2.7 находим координаты точек a, b, c в % (мол.) при t = 60ºC:
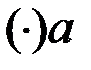 : x ((C2H5)2O) = 85 % (мол.) – состав паровой фазы
: x ((C2H5)2O) = 85 % (мол.) – состав паровой фазы
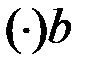 : x ((C2H5)2O) = 70 % (мол.) – состав исходной жидкости
: x ((C2H5)2O) = 70 % (мол.) – состав исходной жидкости
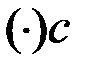 : x ((C2H5)2O) = 62 % (мол.) – состав жидкости
: x ((C2H5)2O) = 62 % (мол.) – состав жидкости
Переведем координаты точек a, b, c из % (мол.) в %(масс.):
% (масс.)= 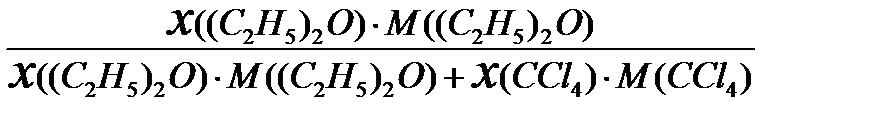
здесь M((C2H5)2O) = 74 г/моль – молярная масса (C2H5)2O;
М(CCl4) = 154 г/моль – молярная масса (CCl4).
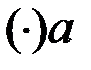 :
: 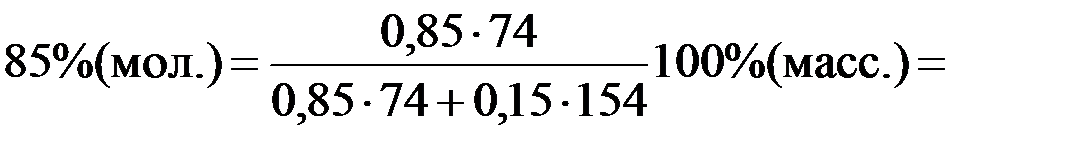
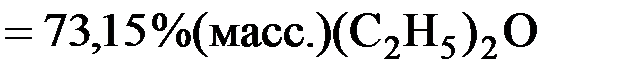 ;
;
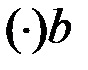 :
: 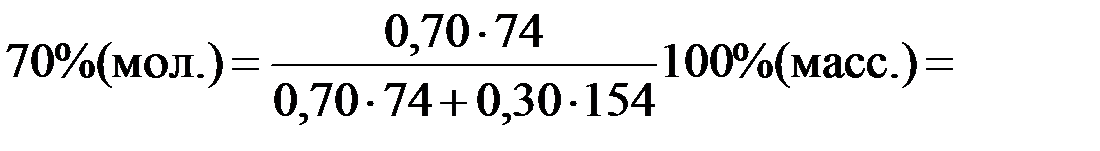
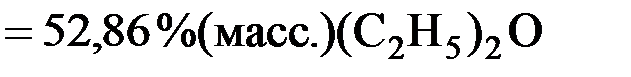 ;
;
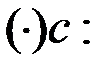
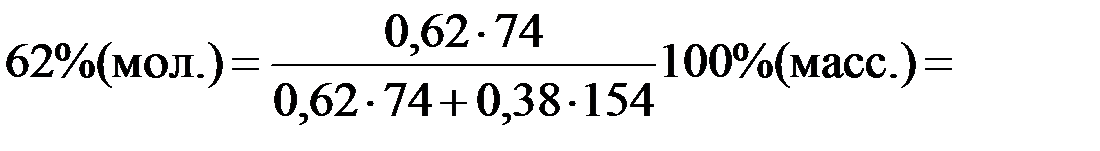
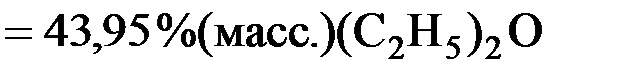
Составляем систему уравнений
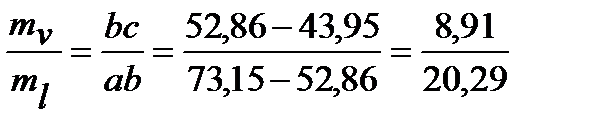
ml + mv = 0,9 кг
и решаем ее методом подстановки:
mv = 0,9 – ml
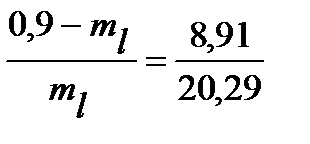
18,261 – 20,29ml = 8,91 ml
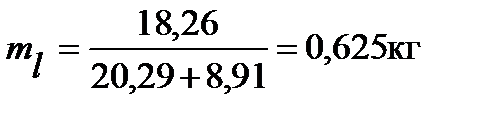
mv = 0,9 – 0,625 = 0,275 кг
Найдем количество каждого компонента в жидкой фазе:
m((C2H5)2O)l = 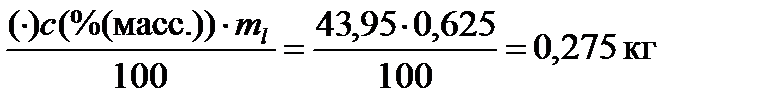
m(CCl4)l = ml – m((C2H5)2O)l = 0,625–0,275 = 0,350 кг
В паре:
m((C2H5)2O)v = 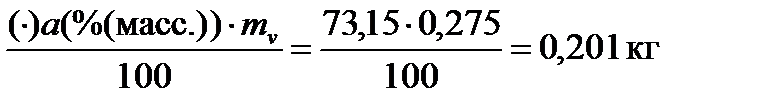
m(CCl4)v = mv – m((C2H5)2O)v = 0,275 – 0,201 = 0,074 кг
Проверим полученные результаты:
m= m((C2H5)2O)l + m(CCl4)l + m((C2H5)2O)v +m(CCl4)v =
= 0,275 + 0,350 + 0,201 + 0,074 = 0,9 кг
Для разделения растворов используют разницу в составах равновесных жидкой и парообразной фаз.
1. Перегонка в равновесии(интегральная перегонка, однократное испарение). В этом виде перегонки пар находится в равновесии с испаряющейся жидкостью. Полного разделения компонентов раствора такой метод не дает. Он позволяет обогатить конденсат одним из компонентов, если не доводить испарение до конца, а остановить его при какой-то температуре. Методом интегральной перегонки можно получить две фракции: дистиллят, обогащенный одним из компонентов, и жидкость, обогащенную другим компонентом (см. рисунки 2.6 и 2.7)
2. Дифференциальная перегонка(постепенное испарение, «простая» перегонка) отличается от интегральной перегонки тем, что образующийся в перегонном кубе пар непрерывно удаляют и конденсируют. Благодаря этому состав системы в перегонном кубе непрерывно изменяется. В условиях отвода пара из перегонного куба испарение жидкости не закончится при температуре конца кипения в интегральной перегонке.
Дифференциальную перегонку можно использовать для разделения исходного бинарного раствора на составляющие его компоненты, если раствор не имеет экстремумов на зависимости температуры кипения от состава раствора. При дифференциальной перегонке систем с минимумом температуры кипения (рисунок 2.4а) в кубовом остатке останется тот жидкий компонент, которым обогащен исходный раствор по сравнению с точкой азеотропа c. При дифференциальной перегонке систем с максимумом температуры кипения (рисунок 2.4б) в кубовом остатке останется азеотропный раствор независимо от состава исходного раствора.
3. Ректификация– это наиболее совершенный способ разделения растворов на основе испарения и конденсации. В этом методе используют принцип противотока неравновесных жидкости и пара, обеспечивая их тесный контакт. В ректификационной колонне на некотором уровне пар, поднимаясь вверх, встречает более холодную жидкость (флегму) и, частично конденсируясь, обогащается одним из компонентов. В итоге выходящий из верхней наиболее холодной части ректификационной колонны охлажденный пар почти целиком состоит из одного из компонентов. Его конденсируют, частично используют для орошения колонны (флегма), а большая часть дистиллята является одним из продуктов разгонки – практически чистым компонентом.
Жидкость, стекая вниз и соприкасаясь с более горячим паром, нагревается, частично испаряется и обогащается другим компонентом. В нижней наиболее нагретой части колонны собирается практически чистый другой компонент.
При ректификации растворов с азеотропами (см. рисунок 2), в отличие от систем без экстремумов на диаграммах Т – x, в чистом виде может быть получен только один из компонентов. В системах с минимумом температуры кипения в нижней части колонны собирается тот практически чистый компонент, которым обогащена исходная жидкость по сравнению с азеотропной точкой; в верхней части колонны собирается пар азеотропного состава, который затем переходит в дистиллят. В системах с максимумом температуры кипения в нижней части колонны собирается раствор азеотропного состава, а в дистиллят переходит тот практически чистый компонент, которым обогащена исходная жидкость по сравнению с азеотропной точкой.
Пример: С помощью диаграммы температура кипения – состав определим, какие продукты можно получить, если подвергнуть раствор (C2H5)2O – CCl4, содержащий 70 % (мол.) (C2H5)2O
а) перегонке в равновесии (интегральной перегонке);
б) простой (дифференциальной) перегонке;
в) ректификации?
Решение:
а) При перегонке в равновесии пар не отводится, а находится в равновесии с жидкостью. Из диаграммы температура кипения – состав раствора (C2H5)2O – CCl4 (рис. 2.5) следует, что при этом состав пара меняется по линии от 89 до 70 мол.% (C2H5)2O, а жидкости – по линии от 70 до 42 мол.% (C2H5)2O .
Чистые вещества в результате такой перегонки получить нельзя, а можно получить 2 фракции: жидкую (в перегонном кубе), обогащенную четыреххлористым углеродом, и дистиллят (конденсированный пар), обогащенный диэтиловым эфиром.
б) При дифференциальной перегонке пар непрерывно отводится. В результате можно получить небольшое количество чистого четыреххлористого углерода.
в) В ректификационной колонне пар, поднимаясь вверх и охлаждаясь, обогащается (C2H5)2O. Вверху колонны и, соответственно, в дистилляте можно получить чистый диэтиловый эфир. Жидкость, стекая вниз и нагреваясь, обогащается ССl4. Внизу колонны будет собираться практически чистый жидкий четыреххлористый углерод.
2.2.2.1 Многовариантное задание № 6 «Анализ фазовых равновесий жидкость – пар в двухкомпонентной системе»
1. Какую информацию о системе несет диаграмма температура кипения – состав заданной в таблице 2.5 системы A–B (рисунки 2.8 –2.22)?
По диаграмме определите:
2. При какой температуре закипит жидкость, содержащая а % вещества A..
3. При какой температуре вся первоначальная жидкость обратится в пар, если при нагревании пар не отводить?
4. Как будет меняться состав первоначальной жидкости по мере испарения?
5. Каков состав первых пузырьков пара?
6. Как изменяется состав равновесного с кипящей жидкостью пара в ходе испарения?
7. Какое количество каждого из компонентов смеси будет находиться в жидкой фазе и в паре, если m кг смеси заданного состава нагреть до температуры t)?
8. Какие продукты можно получить, если подвергнуть жидкость заданного состава:
а) перегонке в равновесии (интегральной перегонке);
б) простой (дифференциальной) перегонке;
в) ректификации?
Таблица 2.5 – Варианты заданий
| Вариант | Система A–B | Масса исходной жидкости m, кг | Состав исходной жидкости и температура | |||||
| Подварианты | ||||||||
| aА, % | t, °C | aА, % | t, °C | aА, % | t, °C | |||
| H2O – C4H8O2 | 2,0 | |||||||
| CH3OH – C2H4Cl2 | 0,5 | |||||||
| CH3CN – H2O | 0,8 | |||||||
| HNO3 – H2O | 1,5 | |||||||
| C6H5CH3 – изо-C4H9OH | 1,2 | |||||||
| HF – H2O | 0,6 | |||||||
| C2H5OH – C2HCl3 | 1,5 | |||||||
| HCOOH – H2O, p = 5,33кПа | 0,8 | |||||||
| H2O – HCOOH | 1,4 | 106,5 | ||||||
| C3H7OH – H2O | 5,0 | |||||||
| C2H5OH – H2O | 2,2 | |||||||
| C5H4O2 – H2O | 1,5 | |||||||
| (C2H5)2O – CCl4 | 2,0 | 72,5 | ||||||
| изо-C3H7OH – H2O | 1,2 | |||||||
| CH3COOH – H2O | 1,3 | |||||||
| H2O – C4H8O2 | 1,5 | |||||||
| CH3OH – C2H5Cl2 | 1,0 | |||||||
| CH3CN – H2O | 1,0 | |||||||
| HNO3 – H2O | 3,0 | |||||||
| C6H5CH3 – изо-C4H9OH | 1,5 | |||||||
| HF – H2O | 2,5 | |||||||
| C2H5OH – C2HCl3 | 2,0 | |||||||
| HCOOH – H2O, p = 5,33кПа | 1,2 | |||||||
| H2O – HCOOH | 1,6 | 106,5 | ||||||
| C3H7OH – H2O | 2,5 | |||||||
| C2H5OH – H2O | 2,0 | |||||||
| изо-С3H7OH – H2O | 2,0 |
Продолжение таблицы 2.5
| Вариант | Система A–B | Масса исходной жидкости m, кг | Состав исходной жидкости и температура | |||||
| Подварианты | ||||||||
| aА, % | t, °C | aА, % | t, °C | aА, % | t, °C | |||
| H2O – C4H8O2 | 2,0 | |||||||
| CH3OH – C2H4Cl2 | 0,5 | |||||||
| CH3CN – H2O | 0,8 | |||||||
| HNO3 – H2O | 1,5 | |||||||
| C6H5CH3 – изо-C4H9OH | 1,2 | |||||||
| HF – H2O | 0,6 | |||||||
| C2H5OH – C2HCl3 | 1,5 | |||||||
| HCOOH – H2O, p = 5,33кПа | 0,8 | |||||||
| H2O – HCOOH | 1,4 | 106,5 | ||||||
| C3H7OH – H2O | 5,0 | |||||||
| C2H5OH – H2O | 2,2 | |||||||
| C5H4O2 – H2O | 1,5 | |||||||
| (C2H5)2O – CCl4 | 2,0 | 67,5 | ||||||
| изо-C3H7OH – H2O | 1,2 | |||||||
| CH3COOH – H2O | 1,3 | |||||||
| H2O – C4H8O2 | 1,5 | |||||||
| CH3OH – C2H5Cl2 | 1,0 | |||||||
| CH3CN – H2O | 1,0 | |||||||
| HNO3 – H2O | 3,0 | |||||||
| C6H5CH3 – изо-C4H9OH | 1,5 | |||||||
| HF – H2O | 2,5 | |||||||
| C2H5OH – C2HCl3 | 2,0 | |||||||
| HCOOH – H2O, p = 5,33кПа | 1,2 | |||||||
| H2O – HCOOH | 1,6 | 106,5 | ||||||
| C3H7OH – H2O | 2,5 | |||||||
| C2H5OH – H2O | 2,0 | |||||||
| изо-С3H7OH – H2O | 2,0 |
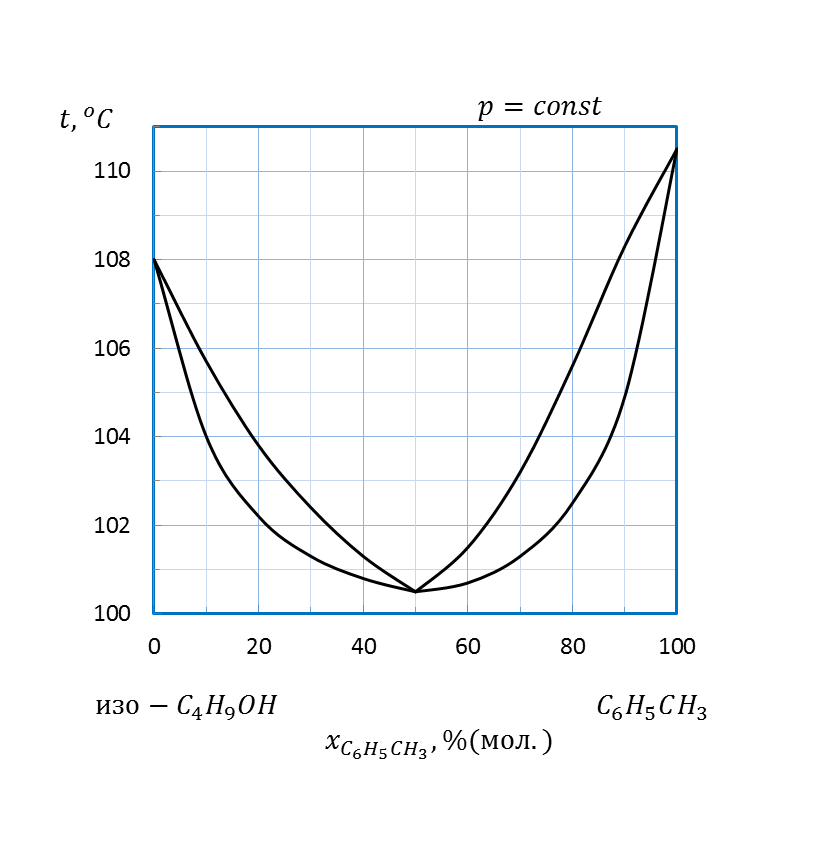
Рисунок 2.8 – Диаграмма состояния температура кипения – состав системы
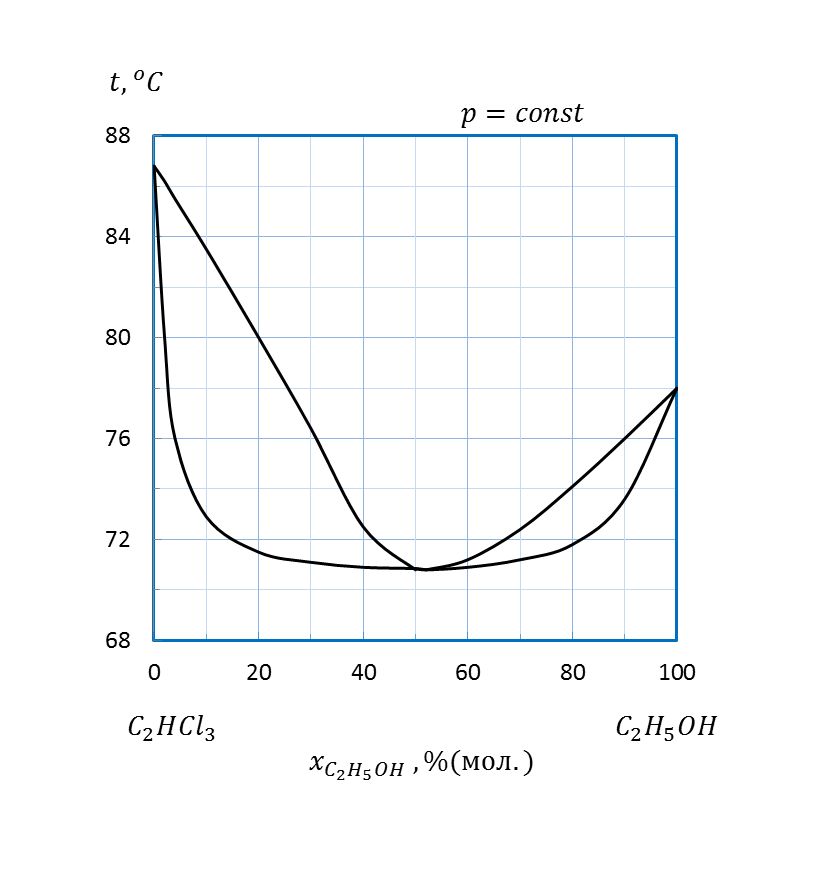
Рисунок 2.9 – Диаграмма состояния температура кипения – состав системы
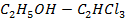

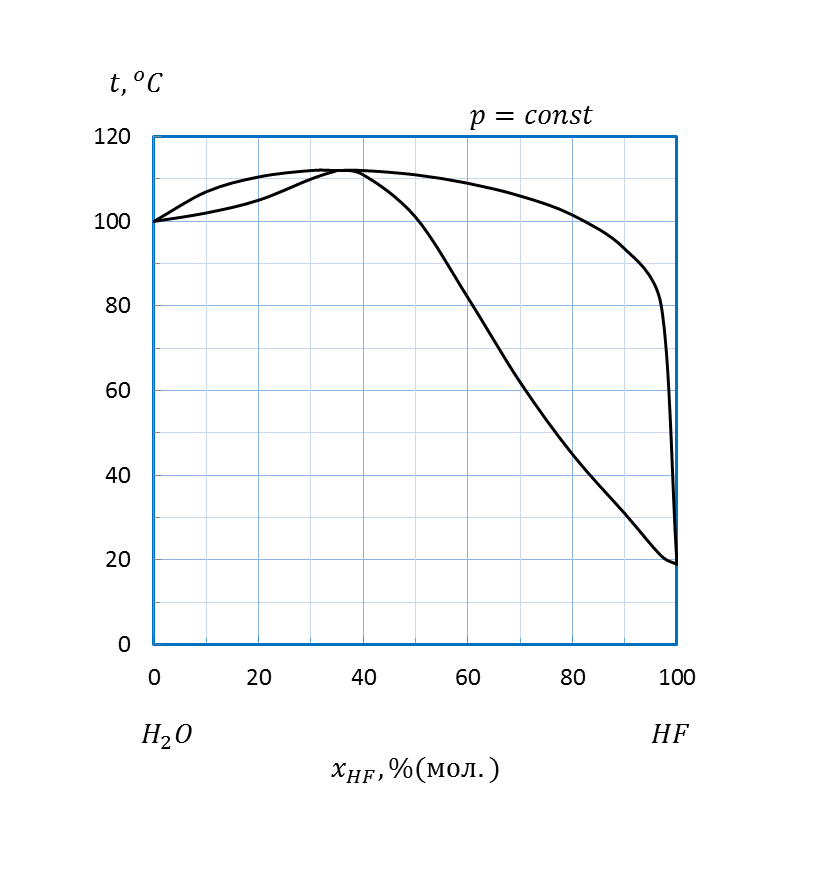
Рисунок 2.10 – Диаграмма состояния температура кипения – состав системы
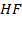
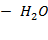
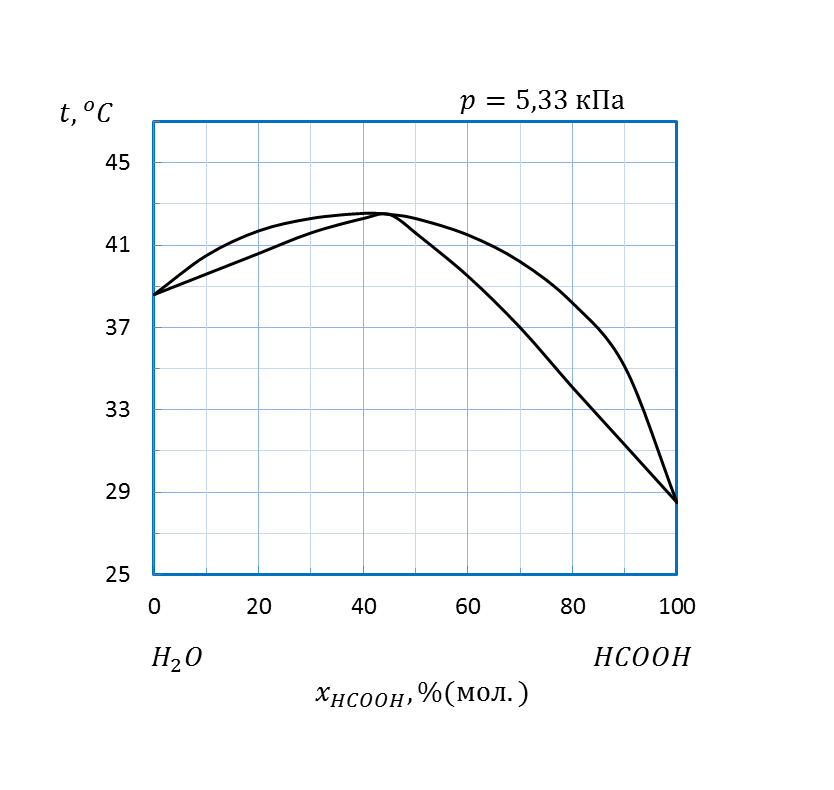
Рисунок 2.11 – Диаграмма состояния температура кипения – состав системы
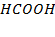
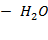 при давлении 5,33 кПа
при давлении 5,33 кПа
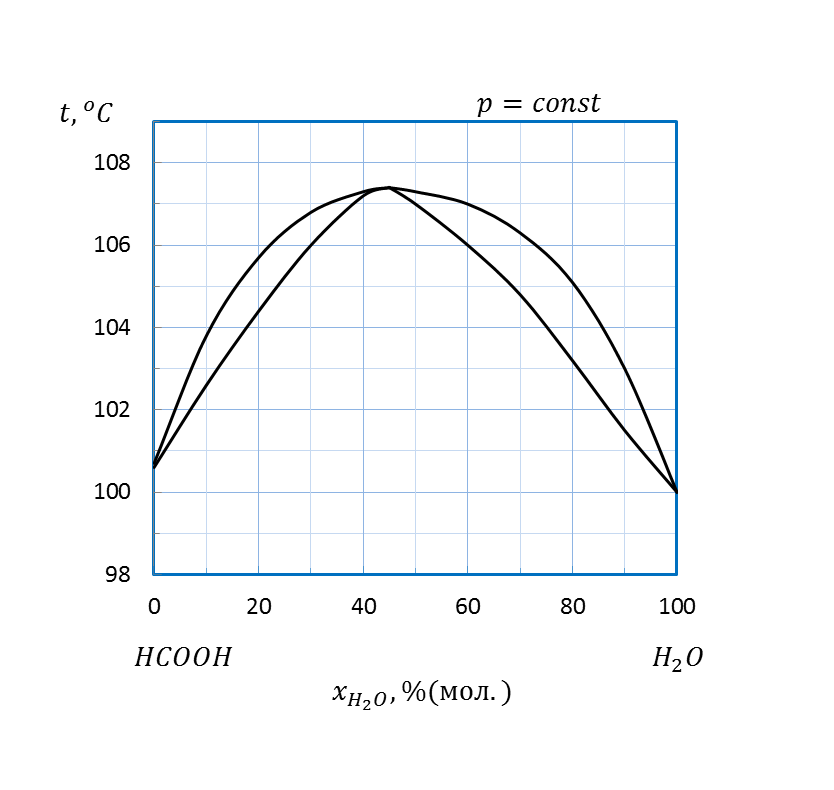
Рисунок 2.12 – Диаграмма состояния температура кипения – состав системы
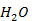
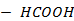
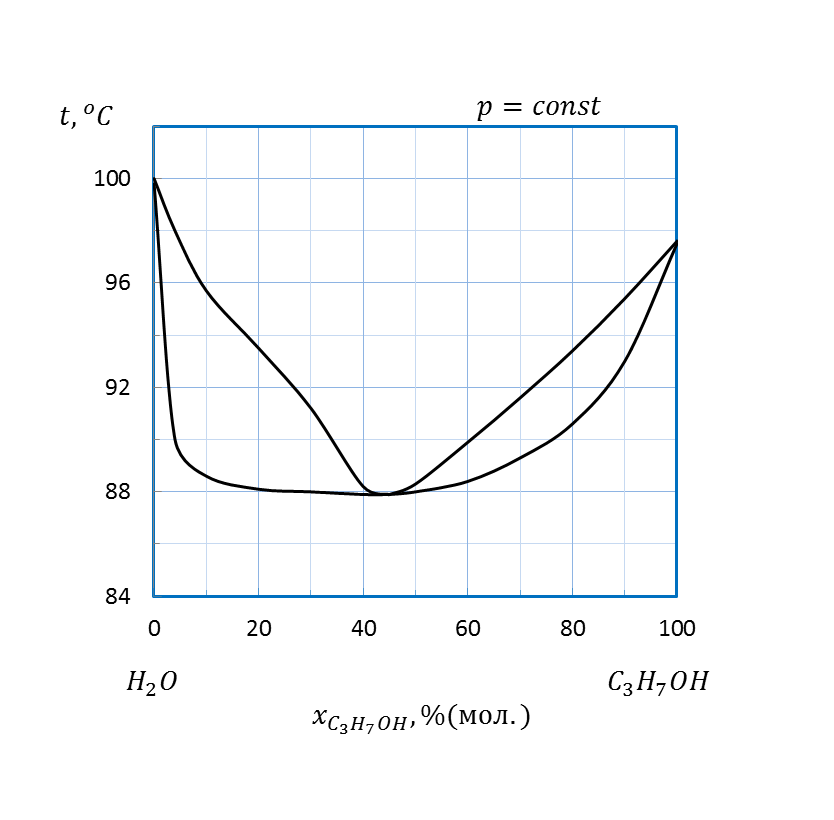
Рисунок 2.13 – Диаграмма состояния температура кипения – состав системы
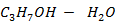
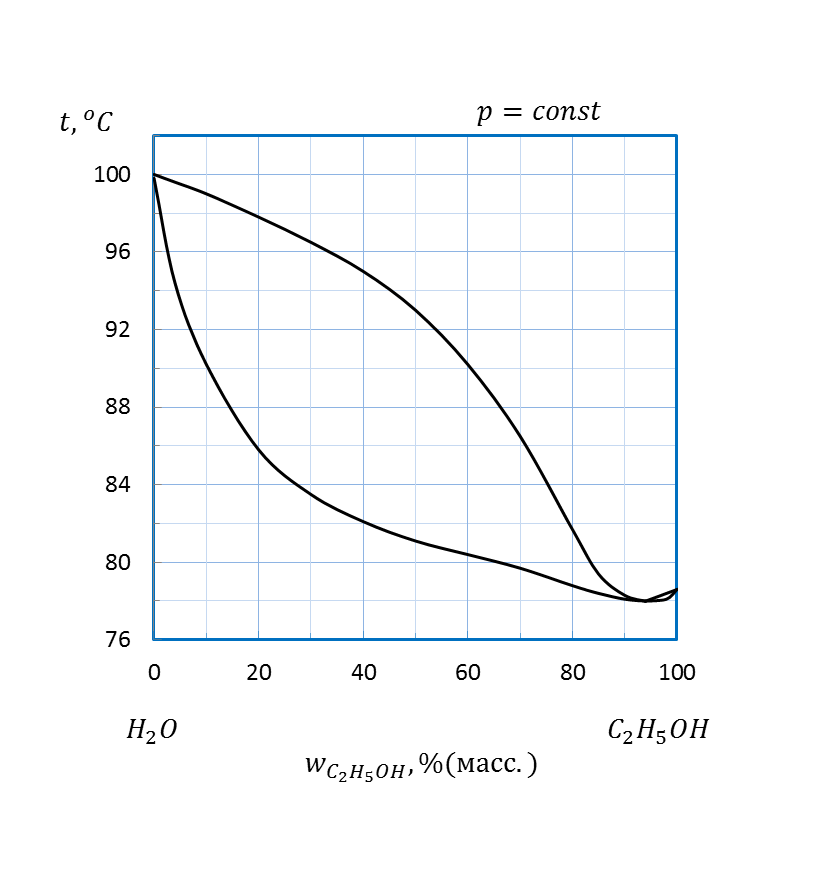
Рисунок 2.14 – Диаграмма состояния температура кипения – состав системы
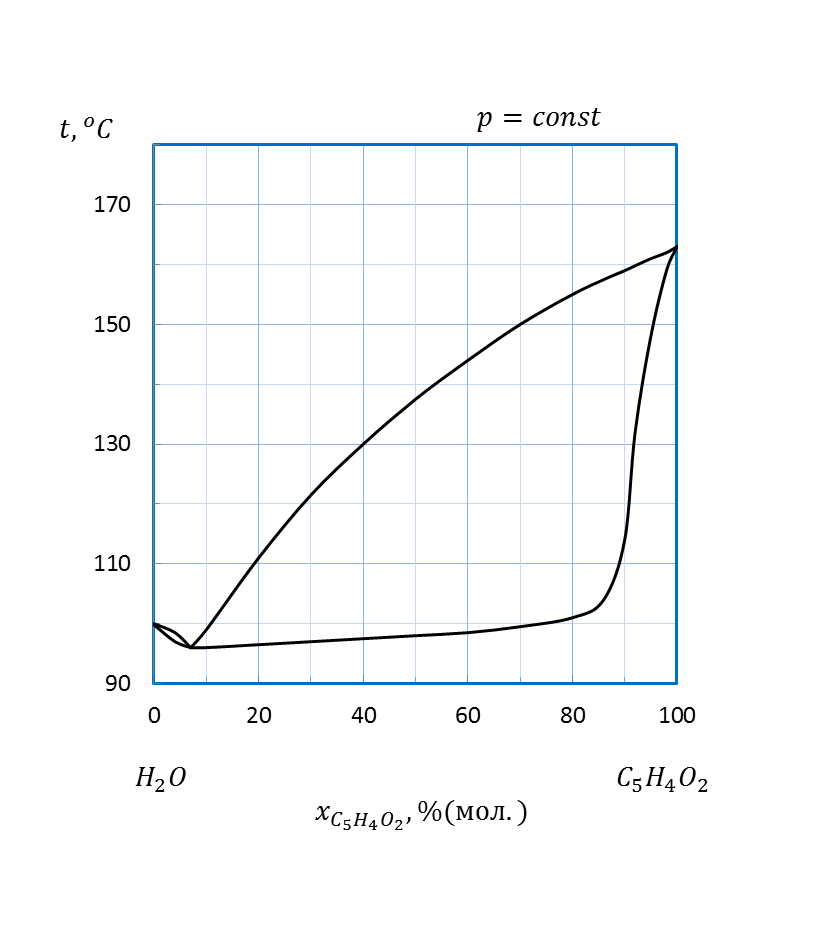
Рисунок 2.15 – Диаграмма состояния температура кипения – состав системы
 (фурфурол - вода)
(фурфурол - вода)
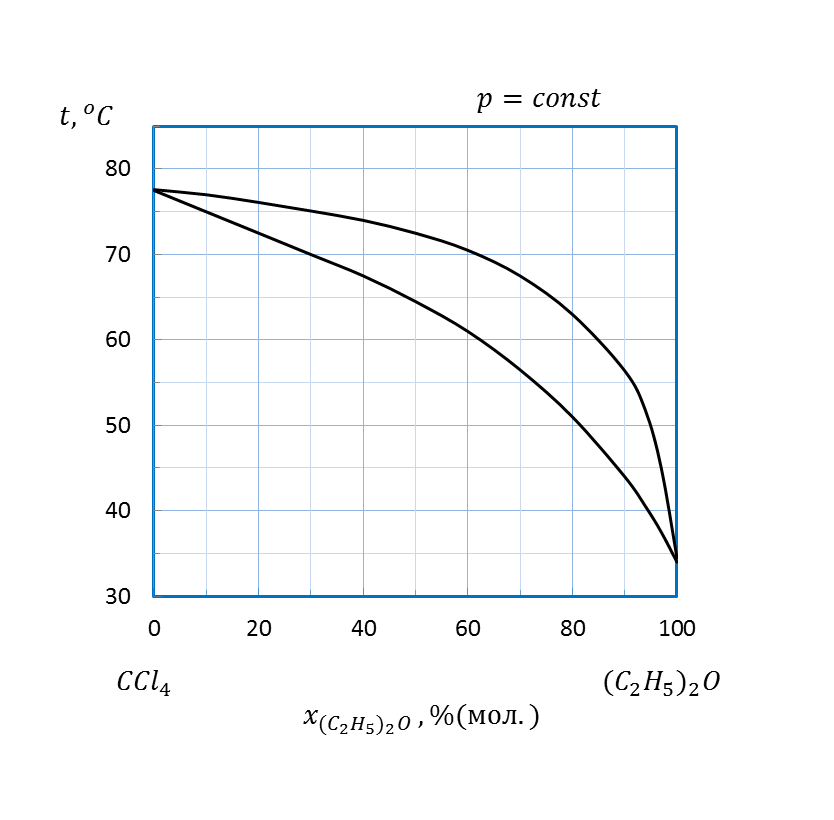
Рисунок 2.16 – Диаграмма состояния температура кипения – состав системы
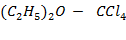 (этиловый эфир - четыреххлористый углерод)
(этиловый эфир - четыреххлористый углерод)
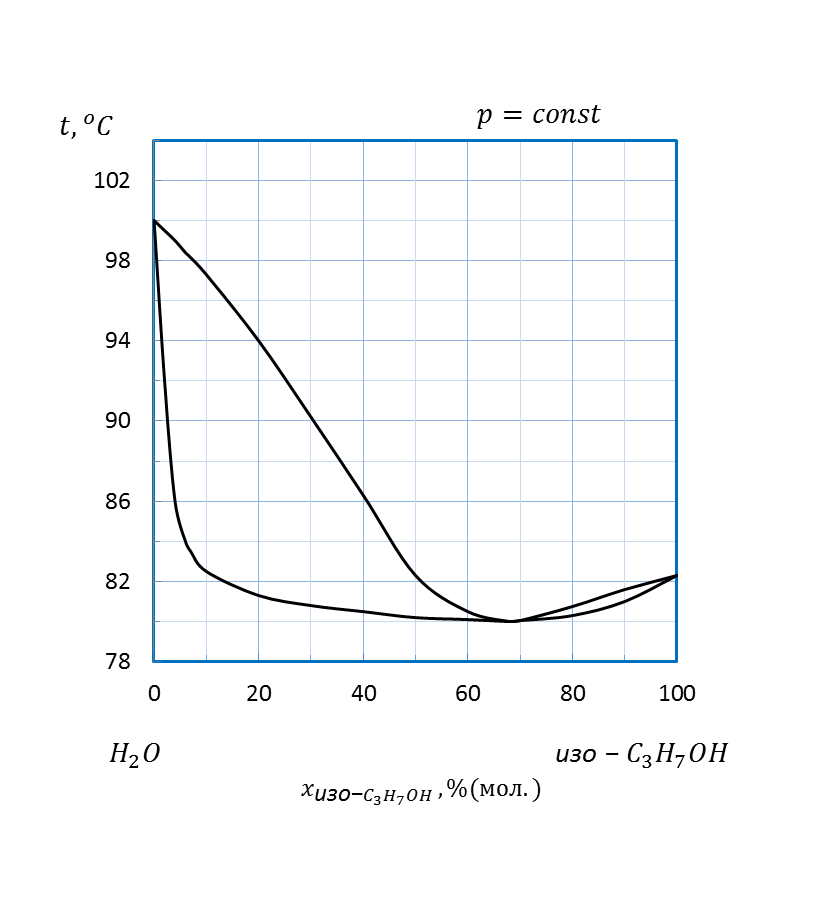
Рисунок 2.17 – Диаграмма состояния температура кипения – состав системы
изо - 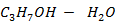
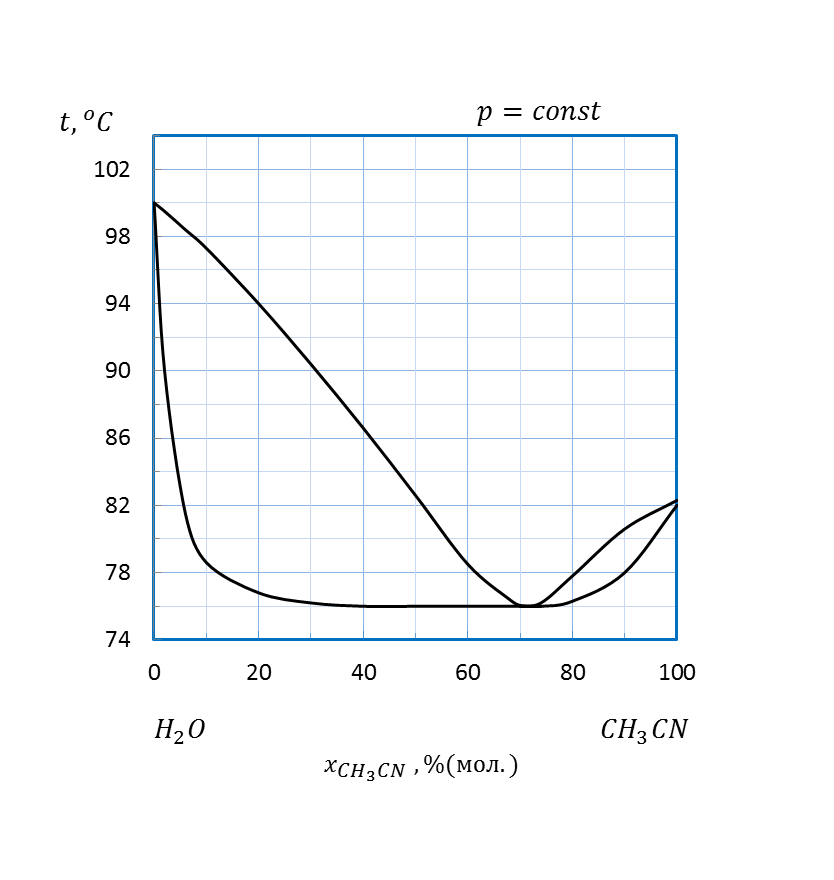
Рисунок 2.18 – Диаграмма состояния температура кипения – состав системы
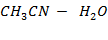
Рисунок 2.19 – Диаграмма состояния температура кипения – состав системы
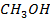
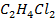
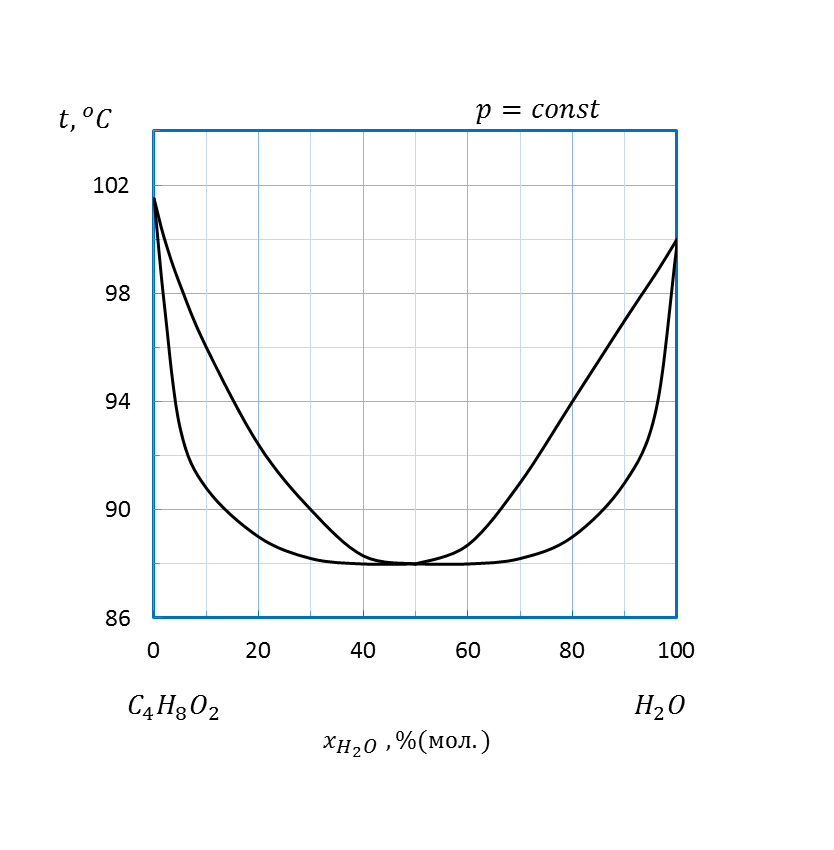
Рисунок 2.20 – Диаграмма состояния температура кипения – состав системы
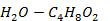 (1,4-диоксан - вода)
(1,4-диоксан - вода)
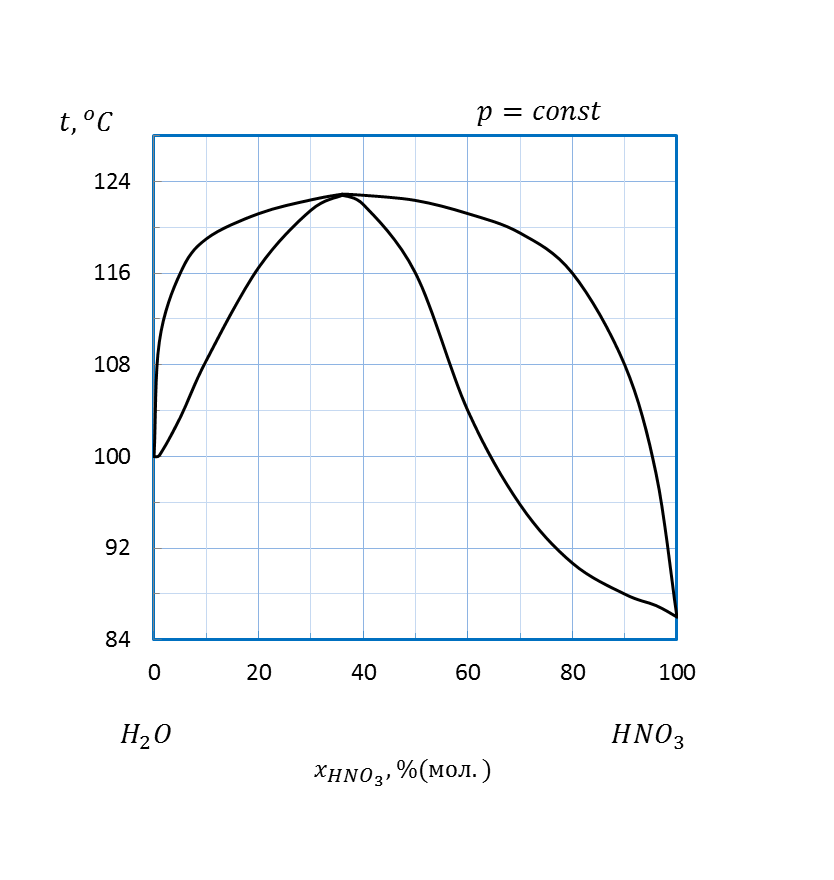
Рисунок 2.21 – Диаграмма состояния температура кипения – состав системы
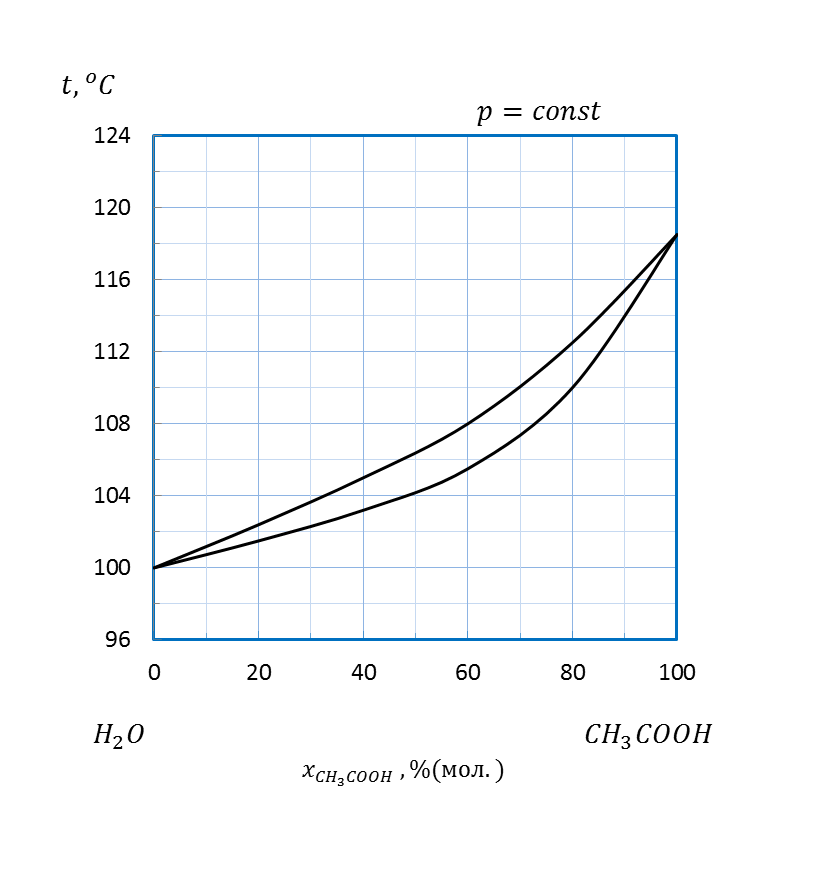
Рисунок 2.22 – Диаграмма состояния температура кипения – состав системы
Дата добавления: 2021-01-26; просмотров: 1224;











