Основные свойства и методы расчета магнитных нелинейных цепей постоянного тока

Содержащие ферромагнитные материалы устройства, предназначенные для создания с помощью намагничивающей силы магнитного потока в определенной части пространства, называют магнитной цепью.

Расчет магнитной цепи заключается в установлении связи между магнитным потоком, током в обмотках, числом витков и геометри­ческими размерами цепи с учетом магнитных свойств материалов, из которых она выполнена.

Законы, используемые при расчете магнитных цепей, базируются на законах электромагнитного поля – законе полного тока и законе непрерывности потока вектора магнитной индукции.

По аналогии с разветвленной электрической цепью магнитная цепь может быть разбита на ветви и узлы. Вследствие нелинейности зависимости индукции магнитного поля от напряженности расчеты магнитной цепи ведут графическими методами, используя законы Кирхгофа:

Первый закон Кирхгофа: алгебраическая сумма магнит­ных потоков в узле равна нулю, .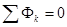

Под узлом разветвленной магнитной цепи здесь подразумевается точка, в которой сходятся три или большее число средних линий маг­нитной индукции. Это понятие является условным, так как размеры поперечных сечений ветвей магнитной цепи соизмеримы с длинами вет­вей. При этом под длинами ветвей магнитной цепи понимаются рассто­яния между соседними узлами вдоль средней линии магнитной индук­ции.

При этом магнитным потокам, направленным к узлу, приписывается один знак (например, положительный), а магнитным потокам, направленным от узла, – противо­положный знак.

Второй закон Кирхгофа: алгебраическая сумма МДС в любом контуре равна алгебраической сумме произведений потоков на соответствующие магнитные сопротивления участков данного контура.

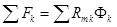
При этом необходимо задаться положительным направ­лением обхода контура.

Обычно рассматривают прямую и обратную задачу расчета магнитной цепи. При решении прямой задачи по заданному магнитному потоку требуется найти МДС. Соответственно, при решении обратной задачи надо по заданной величине МДС найти поток.