Косвенные оценки процессов в линейных непрерывных стационарных системах управления (продолжение).

Косвенные оценки, связанные с распределением полюсов передаточной функции замкнутой системы.

Пусть передаточная функция замкнутой системы не имеет нулей, т.е.

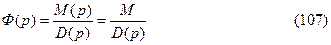
Рассмотрим процесс регулирования при ступенчатом входном воздействии и нулевых начальных условиях. При этом

.

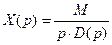Для точного построения 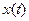нужно знать все корни характеристического уравнения

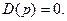
Однако для приближенной оценки процесса достаточно знать область расположения корней, которая будет ограничена либо треугольником либо трапецией.

Для оценки быстродействия может использоваться понятие степени устойчивости η. Под этим понимается модуль вещественной части ближайшего к мнимой оси корня (см. рис. 93.)

Рис.93

Собственные движения, входящие в общий процесс x(t) имеет вид

где 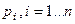-корни характеристического многочлена D(p). Пусть ближайший к мнимой оси корень действительный. В выражении (108) слагаемое 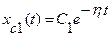затухает наиболее медленно. В большинстве случаев можно считать, что все собственные движения (108), т.е. переходный процесс затухает, когда затухнет это слагаемое. Положив в конце переходного процесса

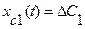
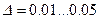, получим, что

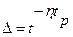
и

При 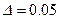из (109) получим

Для случая, когда ближе всего к мнимой оси находится пара комплексно-сопряженных корней может быть получена оценка

.

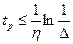Вещественные корни.

В общем случае передаточная функция вида (107), если характеристическое уравнение D(p)=0 имеет все вещественные корни или пару комплексно сопряженных корней, справедливо неравенство

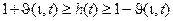
Здесь 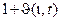- мажоранта h(t), 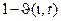- минората. Функция 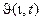определяется из выражения

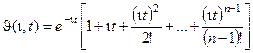
Оценим теперь склонность системы к колебаниям. Колебания будут наблюдаться, если характеристическое уравнение будет иметь комплексные корни вида 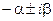. Склонность системы к колебаниям может характеризоваться параметром 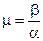- отношение мнимой части корня к вещественной. Чем больше, тем слабее затухают колебания. Покажем это.

Комплексные корни.

Комплексным корням в переходном процессе соответствует слагаемое

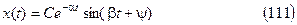
Найдем затухание амплитуды колебания (111) за один период. При некотором t=t₁ имеем

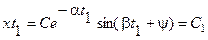
Через период 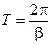имеем

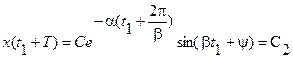
Затуханием за период назовем величину

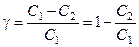
часто она выражается в процентах. Получим

откуда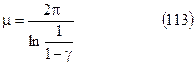

Из выражений (112), (113) видно, что 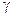увеличивается с уменьшением 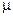и наоборот.

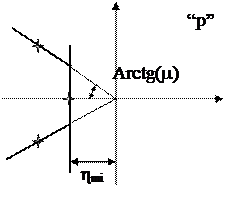Задание определенной колебательности 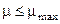ограничивает область возможного расположения корней двумя лучами. Задание степени устойчивости 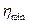добавляет к ним вертикальную прямую. Ограниченная область возможного расположения корней характеристического уравнения с учетом выполнения требования к параметрам 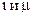показана на рис. 94.

Рис.94

Использование для оценки качества регулирования только корней характеристического уравнения является не совсем верным. Вид переходного процесса определяется не только левой, но и правой частью дифференциального уравнения. Левую часть дифференциального уравнения характеризуют полюсы передаточной функции Ф(p), а правую часть уравнения характеризуют нули передаточной функции Ф(p).

Задание области расположения нулей и полюсов передаточной Ф(p) позволяет более полно оценить вид переходного процесса. Приведем общие рекомендации, которых следует придерживаться при выборе нулей и полюсов Ф(p).

1.Желательно располагать нули вблизи области расположения полюсов. Удаление нулей от области полюсов ведет к увеличению амплитуды собственных колебаний в переходном процессе.

2.Для уменьшения отклонений в переходном процессе часто бывает выгодно удалять полюсы друг от друга.

3.Приблежение полюсов друг к другу не представляет опасности для тех полюсов, которые расположены далеко от мнимой оси.