Методы построения процесса регулирования (продолжение).

Численный расчет процесса регулирования.

Численный расчет процесса регулирования сводится к численному решению уравнения САУ (91). Процесс численного решения дифференциальных уравнений рассмотрен в соответствующих курсах и он не представляет особой сложности, если только правая часть уравнения (91) не имеет разрывов 2-го рода.

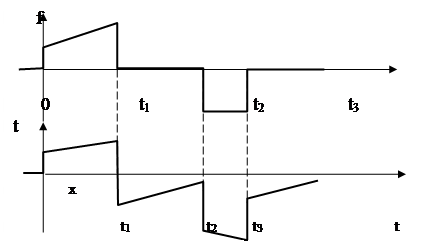
Если в уравнении (91) присутствует дифференцирование входного сигнала и входное воздействие f(t) таково, что правая часть уравнения (91) имеет разрывы 2-го рода, то либо сама переменная, либо некоторые ее производные будут претерпевать разрывы 1-го рода – испытывать скачки. Причем это может происходить не только в начальный момент времени t=0. Эти скачки могут возникать и при t>0, если в эти моменты времени рвутся входной сигнал или его производные. Пример системы и входного сигнала, при которых в сигнале x(t) возникают скачки, представлен на рис. 84.

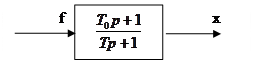Рис.84

Эти скачки методами численного интегрирования дифференциальных уравнений не учитываются, так как эти методы не рассчитаны на наличие разрывов второго рода в правой части дифференциального уравнения (91). Но инженер, ведущий расчет, должен оценить возможность возникновения такой ситуации и принять меры, чтобы, в конечном счете, процесс регулирования был построен правильно.

Оценка возможности возникновения описанной ситуации выполняется достаточно просто. Если в правой части уравнение уравнения (91) возникают разрывы второго рода, т.е. если функция f(t) не является (m-1)-кратно непрерывно дифференцируемой, то скачки необходимо учитывать. Для этого вместо переменной x вводят некоторую другую переменную, которая должна удовлетворять следующим условиям :

- переменная х должна выражаться через эту новую переменную и ее производные;

- уравнение относительно этой новой переменной должно решаться численными методами без отмеченных выше проблем.

Переход к новой переменной в простейшем случае может быть осуществлен анализом структурной схемы и ее простейшими преобразованиями. Кроме того этот переход возможен в результате формальных аналитических преобразований исходного уравнения (91). Ниже мы рассмотрим все эти способы.

Случай наличия разрывов во входном сигнале

Рассмотрим систему, представленную на рис. . При наличии в сигнале f(t) разрывов первого рода переменная х также имеет разрывы первого рода. При этом правая часть уравнения системы

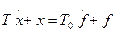
имеет разрывы второго рода.

Преобразуем структурную схему к виду, показанному на рис. 85.

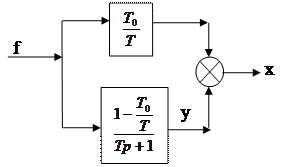Рис. 85.

Примем за неявную переменную y, тогда уравнение системы имеет вид

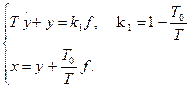
Эта система уравнений может быть проинтегрирована численными методами. Заметим, что при поэлементном описании САУ возможно численное интегрирование системы уравнений без дополнительных преобразований. Например, уравнения системы со следующей структурной схемой (см. рис. 86)

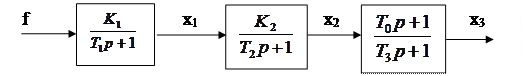Рис.86

при кусочно-непрерывных входных сигналах f(t) переменные х₁, x₂, x₃ изменяются непрерывным образом. В то же время при интегрировании одного дифференциального уравнения 3-ого порядка производная 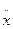имеет разрывы и непосредственно численные методы здесь применятся не могут.

Рассмотрим аналитический способ преобразования уравнения (91).

В операторной форме оно может быть записано в виде

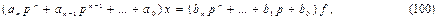
здесь m=n. Представим операторное уравнение в виде

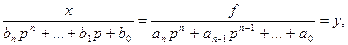(101)

y – новая переменная. Из соотношений (101) имеем

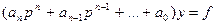(102)

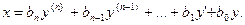(103)

Численное интегрирование уравнения (102) не представляет сложности и может быть выполнено любым известным методом. Зависимость (103) определяет выходную величину САУ по результатам численного интегрирования (102) – через переменную y(t) и ее производные.