Прямая параллельная плоскости.

Рис.9

Прямая параллельна плоскости, если она параллельна какой-либо прямой, лежащей в этой плоскости (рис.9). а║[АВ], а₁║[А₁В₁], а₂║[А₂В₂], задача не имеет единственного решения.

Пересечение прямой с плоскостью.

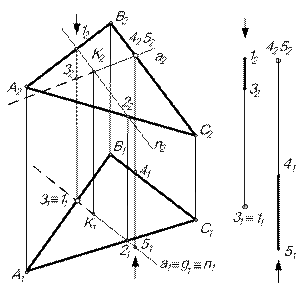
Для определения точки пересечения прямой а с плоскостью общего положения 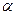(АВС) необходимо выполнить следующие построения (рис.10):

1. Через данную прямую а провести вспомогательную проецирующую плоскость 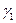, так как

а 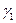, то а .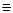

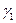2. Построить линию пересечения n данной плоскости 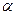(АВС) и вспомогательной плоскости 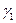. 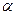(АВС) ∩ 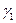=n; [12] n; [1₁2₁] n₁; [1₂2₂] n₂.

3. Определить точку пересечения К прямой а и заданной плоскости К=а∩n; К₁=а₁∩n₁; К₂ а₂.

4. Определяем видимость прямой. Для этого рассматриваем конкурирующие точки 1-3 и 4-5. Точка 1 [AB] 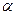(АВС); точка 3 а. На горизонтальной плоскости проекций проекции точек 1₁ и 3₁ совпадают, а на фронтальной плоскости проекций отрезок 1₂3₂ в горизонтальном проецирующем положении. Проекция точки 1₂ [АВ] 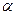(АВС) находится выше проекции 3₂ а. Таким образом на горизонтальной плоскости проекций отрезок прямой до точки К будет закрыт плоскостью.

Рис.11

Рассмотрим конкурирующие точки 4-5; 4 [ВС] 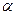(АВС); 5 а. Отрезок [4₁5₁] находится во фронтально-проецирующем положении – на фронтальной плоскости проекций превращается в точку. Таким образом, прямая на фронтальной плоскости проекции будет видна до К₂ , а дальше уходит за плоскость.