Прямая, перпендикулярная плоскости.

Рис.11

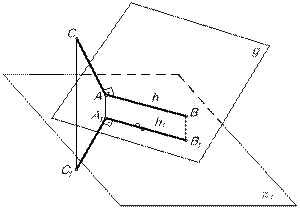
Построение перпендикуляра к плоскости основано на положении геометрии: прямая, перпендикулярная к плоскости, перпендикулярна ко всем прямым, лежащим в этой плоскости и проходящих через точку пересечения перпендикуляра с этой плоскостью (рис.11).

Пусть некоторый отрезок прямой [АС] плоскости и точка А – точка пересечения отрезка прямой с этой плоскостью.

Построим на плоскости горизонтали h и на 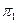– h₁, так как [CA] 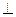[AB], [C₁A₁] 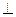[A₁B₁] прямой угол спроецируется на плоскость 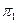без искажения, А₁В₁С₁=АВС.

Если прямая перпендикулярна к плоскости, то ее горизонтальная проекция перпендикулярна горизонтальной проекции горизонтали плоскости, а фронтальная проекция перпендикулярна фронтальной проекции фронтали плоскости.

Расстояние от точки до плоскости измеряется отрезком перпендикуляра от точки до его основания на плоскости:

1. Из точки опустить перпендикуляр на плоскость

2. Найти точку встречи перпендикуляра с плоскостью

Пример 1. Определить расстояние от точки М до плоскости 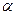(АВС) (рис.12).

1. В плоскости 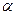(АВС) строим горизонталь и фронталь. Из точки М опускаем перпендикуляр n 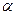(АВС); n₁ 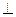h₁, n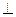₂ f₂.

2. Находим точку пересечения перпендикуляра n с плоскостью 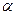(АВС). n 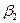; n₂ 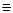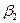; 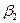∩ 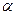(АВС)=m; m₂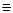 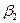; [34] m; n₁∩m₁=К₁ ; К₂ n₂.

3. Определяем истинную величину расстояния от точки М до плоскости 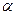(АВС).

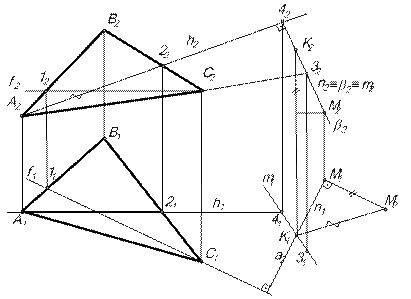
Рис.12

Пример 2. Построить плоскость перпендикулярную данной прямой (рис.13). Так как прямая а 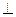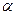(h∩f); а₁ 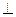h₁; h₂║ОХ; а₂ 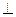f₂; f₁║ОХ .

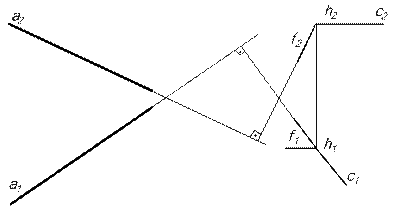
Рис.13

Пример 3. Определить расстояние от точки М до прямой b (рис.14).

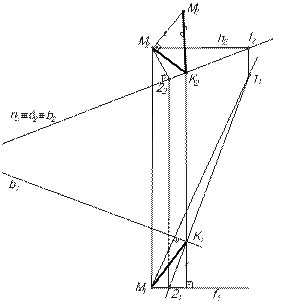
Рис. 14

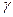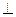1. В точке М задаем плоскость (h∩f) b; h₁ 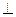b₁; h₂ ∩ОХ; f₂ 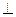b₂; f₁║ОХ.

2. Находим точку пересечения прямой b с заданной плоскостью

b 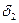; b₂ 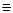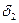; 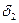∩ 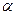(h∩f)=n; n₂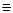 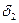; [12] n; n₁∩b₁=K₁; K₂=b₂.

Истинную величину расстояния определяем способом треугольника.