Пересекающиеся плоскости.
ДВЕ ПЛОСКОСТИ. Параллельные плоскости
Две плоскости могут быть параллельны друг к другу или пересекаться между собой.
Параллельные плоскости.
Две плоскости параллельны, если в каждой из них можно построить по две пересекающихся между собой прямые линии так, чтобы прямые одной плоскости были соответственно параллельны прямым другой плоскости.
| |
| Рис.1 | |
Наиболее простой случай – параллельность двух проецирующих плоскостей. Здесь достаточно параллельности следов плоскостей (рис.1).
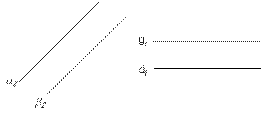
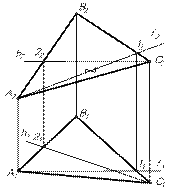
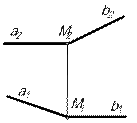
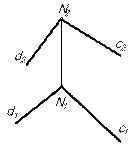
В случае параллельности плоскостей общего положения необходимо в каждой из них указать по две соответственно параллельные прямые (рис.2). В качестве таких прямых можно взять главные линии плоскости или какие-то другие прямые. 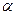 (АВС)║
(АВС)║ 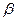 (а ∩ b)║
(а ∩ b)║ 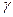 (d ∩ c).
(d ∩ c).
| 
| 
|
 (АВС) (АВС)
| а║h; а1║h1; а2║h2
b║f; b1║f1; b2║f2
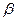 (а ∩ b) (а ∩ b)
| d║[AB]; d1║[A1B1]; d2║[A2B2]
с║[BC]; с1║[B1C1]; с2║[B2C2];
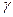 (d ∩ c) (d ∩ c)
|
| Рис.2 |
Пересекающиеся плоскости.
Основная задача – построение линии пересечения двух плоскостей, которая вполне определяется двумя точками, принадлежащими обеим плоскостям:
а) проецирующие
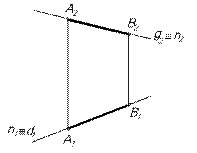
Проецирующие плоскости одного наименования, как перпендикулярные к одной и той же плоскости проекций, пересекаются по прямой линии также перпендикулярной к этой плоскости проекций (рис.3). Проецирующие плоскости разных наименований пересекаются по прямой, для которой они будут проецирующими плоскостями (рис.4).

| 
|
| Рис.3 | Рис.4. |
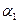 ∩ ∩ 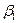 = а = а 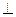 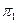 ; ; 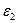 ∩ ∩ 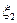 = b = b 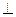 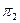
| 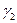 ∩ ∩ 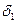 =n; n1 =n; n1 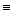 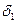 ; n2 ; n2 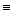 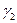
|
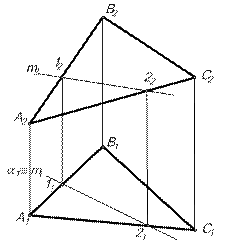
б) Наиболее просто решается задача, если одна из пересекающихся плоскостей проецирующая (рис.5). 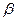 (АВС)∩
(АВС)∩ 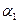 =m; m1
=m; m1 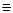
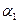 . m – линия пересечения, так как линия пересечения принадлежит и плоскости
. m – линия пересечения, так как линия пересечения принадлежит и плоскости 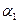 , то 12 лежат на следе плоскости.
, то 12 лежат на следе плоскости.
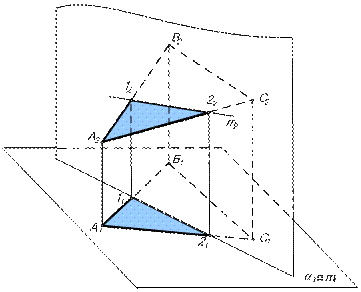
| 
|
| Рис. 5 |
в) Две плоскости общего положения.
Рассмотрим случай пересечения плоскостей общего положения (рис.6).
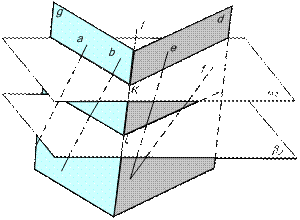
|
| Рис.6 |
Три плоскости пересекаются в одной точке, поэтому общий метод построения точек линии пересечения состоит в следующем: две пересекающиеся плоскости пересекаются третьей, вспомогательной плоскостью.
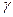 ∩
∩ 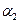 =m;
=m; 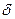 ∩
∩ 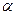 =n; m1∩n1=K1; K2
=n; m1∩n1=K1; K2 
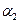
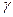 ∩
∩ 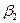 =
= 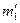 ;
; 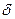 ∩
∩ 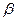 =
= 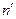 ;
; 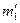 ∩
∩ 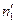 =L1;L2
=L1;L2 
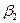 .
.
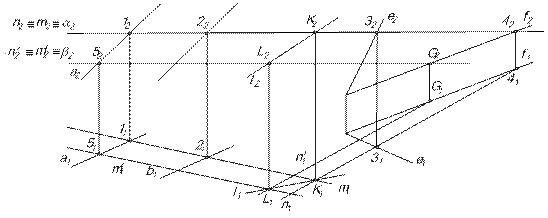
Через точки K и L проводим линию пересечения ℓ (рис.7).
|
| Рис.7 |
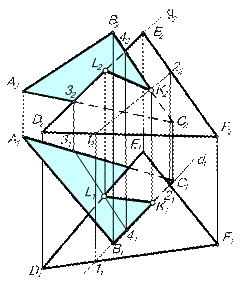
Некоторого упрощения можно достичь, если вспомогательные плоскости проводить через прямые, задающие плоскости (рис.8).  (АВС)∩
(АВС)∩  (DEF)=[LK].
(DEF)=[LK].
|
| Рис.8 |
Дата добавления: 2017-10-04; просмотров: 5210;











