Электрические цепи синусоидального тока
Получение синусоидальных напряжений и токов.
Для получения синусоидальных переменных токов в линейных цепях э. д. с. также должны изменяться по синусоиде.
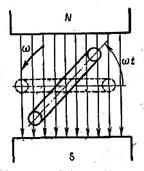
| Простейшим генератором синусоидальной э. д. с. может служить прямоугольная катушка, вращающаяся с постоянной угловой скоростью в однородном магнитном поле вокруг оси, перпендикулярной к направлению линий магнитной индукции. При этом пронизывающий катушку магнитный поток изменяется, и в ней по закону электромагнитной индукции индуктируется э. д. с. Цепь нагрузки подключается к генератору с помощью щеток, наложенных на два кольца, соединенных с катушкой. |
Пусть в начальный момент времени 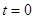 плоскость катушки будет перпендикулярна магнитным линиям. Тогда магнитный поток, пронизывающий катушку, будет иметь максимальное (амплитудное) значение Фm. Если угловая скорость вращения катушки с числом витков w равна ω, то в момент времени t катушка окажется повернутой на угол
плоскость катушки будет перпендикулярна магнитным линиям. Тогда магнитный поток, пронизывающий катушку, будет иметь максимальное (амплитудное) значение Фm. Если угловая скорость вращения катушки с числом витков w равна ω, то в момент времени t катушка окажется повернутой на угол 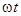 ,и мгновенные значения ее потока и потокосцепления будут равны
,и мгновенные значения ее потока и потокосцепления будут равны 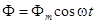 и
и 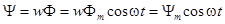 .
.
Тогда мгновенное значение э. д. с. катушки
 .
.
Временные диаграммы
Синусоидально изменяющуюся во времени величину, например ток, имеющий амплитуду (максимальное значение) 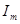 и период повторения Т, можно записать в виде:
и период повторения Т, можно записать в виде: 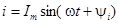
Аргумент синусоидальной функции называют фазовым углом, или фазой:
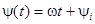 .
.
Угловая частота ωопределяет скорость изменения фазового угла: 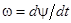 ,рад/с. Угловая частота связана с периодом Т ичастотой f соотношением
,рад/с. Угловая частота связана с периодом Т ичастотой f соотношением 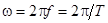 . При фиксированной частоте ω синусоидальную функцию удобно строить в зависимости от переменной
. При фиксированной частоте ω синусоидальную функцию удобно строить в зависимости от переменной 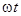 , измеряемой в радианах.
, измеряемой в радианах.
Начальная фаза 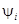 есть значение фазового угла при t = 0.
есть значение фазового угла при t = 0.
На временной диаграммеположительная начальная фаза откладывается от начала координат влево, т. е. в сторону отрицательных значений 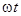 ,а отрицательную начальную фазу следует откладывать в сторону положительных значений
,а отрицательную начальную фазу следует откладывать в сторону положительных значений 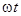 .
.
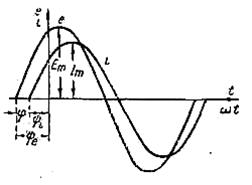
| При совместном рассмотрении двух синусоидальных функций одной частоты разность их фаз, равную разности их начальных фаз, часто называют углом сдвига и обычно обозначают φ. Так, разность фаз ЭДС 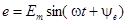 и тока и тока 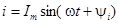 или, иначе, угол сдвига кривой тока относительно кривой ЭДС будет или, иначе, угол сдвига кривой тока относительно кривой ЭДС будет 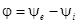 . Если синусоидальные функции одной частоты имеют одинаковые начальные фазы, то говорят, что они совпадают по фазе, а если разность их фаз равна . Если синусоидальные функции одной частоты имеют одинаковые начальные фазы, то говорят, что они совпадают по фазе, а если разность их фаз равна 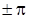 ,то говорят, что они противоположны по фазе. ,то говорят, что они противоположны по фазе.
|
Векторные диаграммы
Такое изображение можно рассматривать не только как источник дополнительной информации о цепи, но и непосредственно использовать для решения некоторых задач. Рассмотрим, как можно применить вращающийся вектор для изображения синусоидальной ЭДС 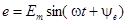 .
.
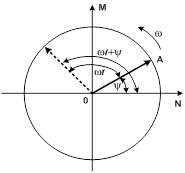
Возьмем прямоугольную систему осейNOMи условимся откладывать положительные углы против направления часовой стрелки.
Расположим под углом 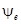 к оси ON вектор ОА, длина которого в выбранном масштабе равна амплитуде ЭДС к оси ON вектор ОА, длина которого в выбранном масштабе равна амплитуде ЭДС 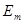 . Будем вращать этот вектор в положительном направлении с постоянной угловой скоростью, равной угловой частоте ω. По истечении промежутка времени t вектор ОА повернется на угол . Будем вращать этот вектор в положительном направлении с постоянной угловой скоростью, равной угловой частоте ω. По истечении промежутка времени t вектор ОА повернется на угол 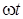 и составит с осью ON угол и составит с осью ON угол 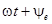 . Тогда величина его проекции на ось OM в принятом масштабе даст значение ЭДС для момента времени t: . Тогда величина его проекции на ось OM в принятом масштабе даст значение ЭДС для момента времени t: 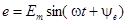 . .
| 
|
Полный цикл изменений ЭДС получится за один полный оборот вектора ОА.
Таким образом, можно условиться изображать синусоидальную функцию вектором, длина которого определяется ее амплитудным значением, а направление – ее начальной фазой, при этом положительная начальная фаза откладывается от горизонтальной оси в сторону вращения векторов. В результате получается векторная диаграмма.
Векторные диаграммы особенно удобны при сложении или вычитаний синусоид одинаковой частоты, Как известно, результатом будет также синусоида той же частоты. При сложении нескольких синусоид нужно складывать их мгновенные значения, т; е. проекции векторов, изображающих эти синусоиды, но так как сумма проекций векторов на какую-либо ось равна проекции геометрической суммы этих векторов на ту же ось, то эта геометрическая сумма и будет вектором, изображающим результирующую синусоиду. Длина вектора даст амплитуду результирующей синусоиды, угол с горизонтальной осью – ее начальную фазу.
Параметры цепей переменного тока
1. Пусть через активное сопротивление протекает синусоидальный ток
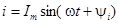 , тогда
, тогда 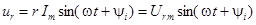
Следовательно, в цепи с сопротивлением r напряжение и ток совпадают по фазе. 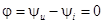 .
.
2. Пусть через индуктивное сопротивление протекает синусоидальный ток
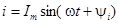 , тогда
, тогда 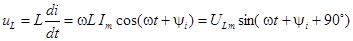
Следовательно, в цепи с индуктивностью L напряжение опережает ток по фазе на 90°. 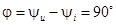 .
.
 – индуктивное сопротивление (x – обозначает реактивное сопротивление в отличие от активного r).
– индуктивное сопротивление (x – обозначает реактивное сопротивление в отличие от активного r). 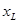 учитывает реакцию самоиндукции (ЭДС самоиндукции, возникающей в катушке при протекании синусоидального тока).
учитывает реакцию самоиндукции (ЭДС самоиндукции, возникающей в катушке при протекании синусоидального тока).
3. Пусть через емкостное сопротивление протекает синусоидальный ток
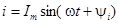 , тогда
, тогда
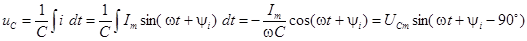
Следовательно, в цепи с емкостью С напряжение отстает от тока по фазе на 90°. 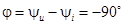 .
.
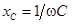 – емкостное сопротивление (тоже реактивное), учитывающее реакцию емкости на протекание переменного тока.
– емкостное сопротивление (тоже реактивное), учитывающее реакцию емкости на протекание переменного тока.
Действующие и средние значения периодических ЭДС и токов
Так как тепловое действие тока пропорционально квадрату этого тока, то о величине периодических токов и ЭДС в технике обычно судят по их средним квадратичным значениям за полный период.
Понятие о среднем квадратичном значении можно получить, рассматривая тепловое действие тока. Пусть сопротивление цепи, в которой протекает периодический ток, равно r. Тогда по закону Джоуля – Ленца количество тепла, выделяемое в этой цепи током за элементарный промежуток времени dt, будет 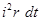 , а за каждый полный период
, а за каждый полный период 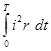 .
.
Обозначим через I такой постоянный ток, который за этот промежуток времени Т выделит в сопротивлении r такое же количество тепла. Тогда имеем:
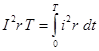 , откуда
, откуда 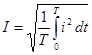 .
.
Величина I, определяемая последним равенством, называется действующим или средним квадратичным значением периодического тока.
Для синусоидального тока имеем: 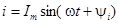 и, следовательно,
и, следовательно,
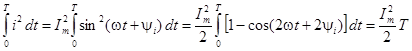 .
.
так интеграл от второго слагаемого равен нулю. Окончательно для действующего значения синусоидального тока получим
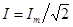 .
.
Аналогично определяется действующее значение Е периодической ЭДС:
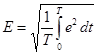 .
.
Для действующего значения синусоидальной ЭДС: 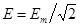 .
.
Приборы, применяемые для измерения периодических ЭДС и токов, обычно дают их действующие значения.
Кроме средних квадратичных значений периодических ЭДС и токов, используют их средние арифметические значения.
Под средними арифметическими или просто средними значениями ЭДС и тока за промежуток времени от t1до t2понимают, соответственно, величины:
 и
и 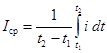 .
.
Для синусоидальных ЭДС и токов среднее значение за полный период равно нулю, так как площади положительной и отрицательной полуволн синусоиды равны по величине и противоположны по знаку. Обычно для таких ЭДС и токов под средним значением понимают среднее значение, соответствующее положительной полуволне. В этом случае:
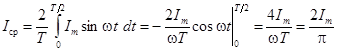 .
.
Аналогично 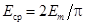 .
.
Дата добавления: 2019-12-09; просмотров: 505;











