Метод эквивалентного источника
Теоремы компенсации
Теорема Тевенена:
Токи и напряжения в линейной цепи не изменятся, если ветвь заменить источником напряжения, ЭДС которого равна падению напряжения на этой ветви, а направление противоположно направлению заменяемого напряжения.
Теорема Нортона:
Токи и напряжения в линейной цепи не изменятся, если ветвь заменить источником тока, ток которого равен току в этой ветви и совпадает с направлением тока в ветви.
Метод эквивалентного источника
Этот метод применяется для определения тока (или напряжения)
в сопротивлении (проводимости) одной ветви сложной цепи. Если эта
ветвь содержит источники энергии, их следует считать принадлежащими к остальной части сложной цепи.
| Предположим, что нам требуется найти ток в некоторой ветви сложной цепи. Выделим на рисунке эту ветвь, а всю остальную часть цепи условно обозначим прямоугольником А. («А» - активная часть цепи, содержит источники ЭДС) | 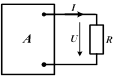
|
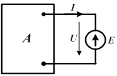
Сопротивление R исследуемой ветви в соответствии с теоремой Тевенена заменяется эквивалентной ЭДС 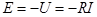 где I и U – искомые ток и напряжение, совпадающие по направлению. где I и U – искомые ток и напряжение, совпадающие по направлению.
| 
|
После этого применяется метод наложения.
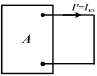
Сначала принимаются в расчет все источники энергии активного двухполюсника, а ЭДС Е замыкается накоротко. Тогда ток 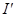 ветви равен, очевидно, току ветви равен, очевидно, току 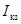 короткого замыкания активного двухполюсника, и совпадает по направлению с током I. короткого замыкания активного двухполюсника, и совпадает по направлению с током I.
| 
|
| Затем учитывается только ЭДС Е. При этом источники энергии, включенные в активный двухполюсник, заменяются их внутренними. В частности, идеальные источники напряжения замыкаются накоротко, а идеальные источники тока – размыкаются. | 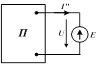
|
Активный двухполюсник превращается в пассивный П.Пусть эквивалентная проводимость этого двухполюсника относительно его зажимов равна GB. Тогда ток ветви для этого этапа, если считать его направление совпадающим с 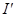 , равен
, равен 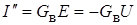 .
.
Действительный ток исследуемой ветви с проводимостью 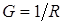 равен алгебраической сумме токов обоих этапов:
равен алгебраической сумме токов обоих этапов:
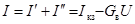 .
.
С другой стороны по закону Ома 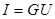 .
.
Откуда 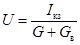 .
.
Если сопоставить эту формулу с выражением для напряжения источника тока, то можно сделать следующий вывод:
активный двухполюсник эквивалентен источнику тока с внутренним током, равным току короткого замыкания двухполюсника, и с внутренней проводимостью, равной проводимости этого же двухполюсника, но без источников энергии.
Из полученного выражения следует, что при холостом ходе, т. е. при 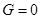 , напряжение на выходных зажимах двухполюсника будет:
, напряжение на выходных зажимах двухполюсника будет:
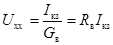
Искомый ток
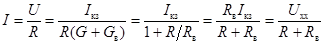
Из аналогии этой формулы с выражением для тока, создаваемого источником напряжения, видно, что
активный двухполюсник эквивалентен источнику напряжения с ЭДС, равной напряжению холостого хода на зажимах разомкнутого двухполюсника и внутренним сопротивлением, равным сопротивлению этого же двухполюсника, но без источников энергии.
Можно предложить следующий алгоритм метода эквивалентного генератора:
1. Изъять ветвь, в которой надо определить ток, заменив ее разностью потенциалов.
2. Любым известным методом, например методом узловых напряжений, определить указанную разность потенциалов (т.е. напряжение холостого хода).
3. Определить входной сопротивление соответствующего пассивного двухполюсника со стороны разомкнутых зажимов.
4. Возвращаясь к исходной схеме записать ток в искомой ветви.
Дата добавления: 2019-12-09; просмотров: 899;











