Вопрос 4. Закон Стефана-Больцмана. Законы Вина.
Физики C. Ленгли, Э. Прингсгейм, О. Люммер, Ф. Курлбаум и др., исследуя экспериментально распределение энергии излучения АЧТ по спектру, определили излучательные способности абсолютно черного тела R(λ,T) и R(ν,T). Результаты таких экспериментов при различных значениях температуры приведены на рис. 16.4.
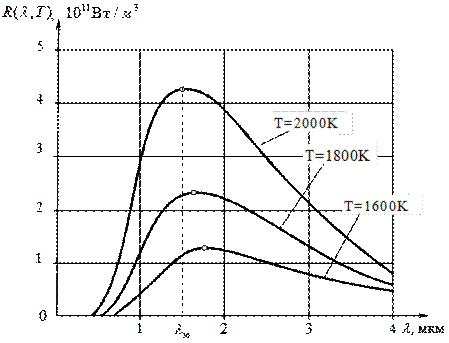
Рис. 16.4
В результате экспериментальных и теоретических исследований, выполненных Й. Стефаном и Л. Больцманом был получен важный закон теплового излучения абсолютно черного тела. Этот закон утверждает, что энергетическая светимость абсолютно черного тела пропорциональна четвертой степени его абсолютной температуры, то есть
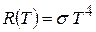 . (16.10)
. (16.10)
По современным измерениям постоянная Стефана-Больцмана
σ = 5,6686·10-8 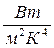 .
.
Для реальных тел закон Стефана-Больцмана выполняется лишь качественно, то есть с ростом температуры энергетические светимости всех тел увеличиваются. Однако, для реальных тел зависимость энергетической светимости от температуры уже не описывается простым соотношением (16.7), а имеет вид:
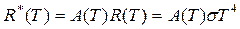 . (16.11)
. (16.11)
Коэффициент А(T) в (16.11), всегда меньший единицы, можно назвать интегральной поглощательной способностью тела. Значения коэффициента А(T) известны для многих технически важных материалов. Так, в достаточно широком диапазоне температур для металлов А(T) = 0,1 ÷ 0,4, а для угля и окислов металлов А(T) = 0,5 ÷ 0,9.
Энергетическая светимость 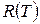 АЧТ, численно равная площади под соответствующими кривыми, сильно зависит от температуры. Максимум излучательной способности с увеличением температуры смещается в сторону коротких длин волн.
АЧТ, численно равная площади под соответствующими кривыми, сильно зависит от температуры. Максимум излучательной способности с увеличением температуры смещается в сторону коротких длин волн.
Закон Стефана-Больцмана не дает информации о спектральном составе излучения абсолютно черного тела.
В 1893 г. немецкий физик В.Вин теоретически рассмотрел термодинамический процесс сжатия излучения, заключенного в полости с идеально зеркальными стенками, и пришел к выводу, что испускательная способность абсолютно черного тела прямо пропорциональна кубу частоты и является функцией отношения ν/T:
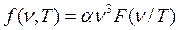 , (16.12)
, (16.12)
где α – постоянная величина, F - некоторая функция, конкретный вид которой термодинамическими методами установить невозможно.
Переходя в этой формуле Вина от частоты к длине волны, получим:
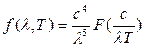 . (16.13)
. (16.13)
Как видно, в выражение для излучательной способности 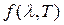 температура входит лишь в виде произведения λT. Уже это обстоятельство позволило предсказать некоторые особенности функции
температура входит лишь в виде произведения λT. Уже это обстоятельство позволило предсказать некоторые особенности функции 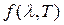 . В частности, эта функция достигает максимума при определенной длине волны λm, которая при изменении температуры тела изменяется так, чтобы выполнялось условие: λmT = const.
. В частности, эта функция достигает максимума при определенной длине волны λm, которая при изменении температуры тела изменяется так, чтобы выполнялось условие: λmT = const.
Таким образом, В. Вин сформулировал закон теплового излучения, согласно которому длина волны λm, на которую приходится максимум излучательной способности абсолютно черного тела, обратно пропорциональна его абсолютной температуре. Этот закон можно записать в виде
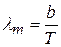 , (16.14)
, (16.14)
где 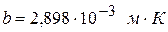 - постоянная Вина.
- постоянная Вина.
Закон Вина называют законом смещения, подчеркивая тем самым, что при повышении температуры абсолютно черного тела положение максимума его излучательной способности смещается в область коротких длин волн. Результаты экспериментов, приведенные на рис. 16.4, подтверждают этот вывод не только качественно, но и количественно, строго в соответствии с формулой (16.14).
С ростом температуры любого тела длина волны, вблизи которой тело излучает больше всего энергии, также смещается в сторону коротких длин волн. Это смещение, однако, уже не описывается простой формулой (16.14), которую для излучения реальных тел можно использовать только в качестве оценочной, т.е. формула (16.14) остается в силе только при больших частотах и низких температурах.
Кроме закона смещения (16.14) Вин получил выражение для максимального значения излучательной способности АЧТ. Эту зависимость называют вторым законом Вина, согласно которому максимальное значение испускательной способности АЧТпрямо пропорционально абсолютной температуре в пятой степени:
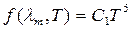 , (16.15)
, (16.15)
где 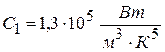 . Однако, получить теоретическое выражение для универсальной функции Кирхгофа, хорошо описывающее экспериментальные результаты во всем диапазоне длин волн излучения тела, Вину не удалось.
. Однако, получить теоретическое выражение для универсальной функции Кирхгофа, хорошо описывающее экспериментальные результаты во всем диапазоне длин волн излучения тела, Вину не удалось.
Во всех разобранных выше случаях подход к изучению теплового излучения был термодинамическим. У.Рэлей и Д.Джинс впервые к этим явлениям применили методы классической статистической физики. Согласно закону о равномерном распределении энергии равновесной системы по степеням свободы на каждую колебательную степень свободы осциллятора с собственной частотой ν приходится энергия, равная < 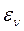 > = kT, где k −постоянная Больцмана. В соответствии с таким подходом У.Рэлей и Д.Джинс в 1905 г. получили выражение для универсальной функции Кирхгофа:
> = kT, где k −постоянная Больцмана. В соответствии с таким подходом У.Рэлей и Д.Джинс в 1905 г. получили выражение для универсальной функции Кирхгофа:
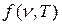 =
= 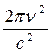 kT. (16.16) Здесь
kT. (16.16) Здесь  − общее число степеней свободы системы, приходящихся на единицу объема полости.
− общее число степеней свободы системы, приходящихся на единицу объема полости.
Однако, как показал опыт, формула Рэлея – Джинса хорошо согласуясь с опытными данными только для малых частот (рис.16.5) и больших температур, не удовлетворяет закону смещения Вина, а также закону Стефана-Больцмана. Действительно, для абсолютно черного тела энергетическая светимость R(T), определяемая по формуле Рэлея−Джинса (16.16), оказывается равной бесконечности:

Рис. 16.5
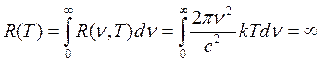 .
.
Согласно закону Стефана-Больцмана (1.10) энергетическая светимость 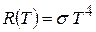 т.е. является конечной величиной. Поскольку вывод формулы (16.16) был безупречным в своей классической строгости и последовательности, решение проблемы описания теплового излучения в рамках классической физики оказалось невозможным в принципе. Это обстоятельство получило в физике образное название «ультрафиолетовая катастрофа». Причина вышеуказанных трудностей, возникших при отыскании вида функции Кирхгофа, связана с одним из основных положений классической физики, согласно которому энергия любой системы может изменяться непрерывно, т.е. может принимать любые сколь угодно близкие значения.
т.е. является конечной величиной. Поскольку вывод формулы (16.16) был безупречным в своей классической строгости и последовательности, решение проблемы описания теплового излучения в рамках классической физики оказалось невозможным в принципе. Это обстоятельство получило в физике образное название «ультрафиолетовая катастрофа». Причина вышеуказанных трудностей, возникших при отыскании вида функции Кирхгофа, связана с одним из основных положений классической физики, согласно которому энергия любой системы может изменяться непрерывно, т.е. может принимать любые сколь угодно близкие значения.
Вопрос 5. Формула Планка.
Выход из создавшейся ситуации нашел немецкий физик М. Планк.
В 1900 г. он впервые выдвинул гипотезу о дискретных значениях энергии осциллятора.
Согласно этой гипотезе энергия осциллятора с собственной частотой ν может принимать лишь определенные дискретные (квантованные) значения, отличающиеся на целое число элементарных порций − квантов энергии: εν = hν, где h= 6,625·10-34 Дж·с − постоянная Планка (квант действия). Тогда полная энергия осциллятора будет равна целому числу квантов
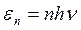 , (
, ( 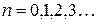 ). (16.17)
). (16.17)
Согласно этой гипотезе Планк моделировал реальное твердое тело с помощью системы квантовых осцилляторов. Выполнив усреднение энергии осциллятора с помощью распределения Больцмана, Планк получил выражение для среднего значения энергии, приходящейся на одну колебательную степень свободы осциллятора:
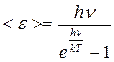 . (16.18)
. (16.18)
Подставив соотношение (16.18) в формулу Рэлея – Джинса (16.14), Планк получил формулу для излучательной способности АЧТ как функцию от частоты излучения:
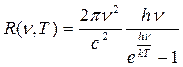 . (16.19)
. (16.19)
Эта формула как функция от длины волны излучения имеет вид:
 , (16.20)
, (16.20)
именно ее чаще всего используют в экспериментальных работах.
Из формулы Планка вытекают все законы теплового излучения тел.
В области малых частот, т.е. при условии, что квант энергии во много раз меньше средней энергии осциллятора (h 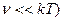 , формула Планка совпадает с формулой Релея—Джинса. Для доказательства этого разложим функцию eh
, формула Планка совпадает с формулой Релея—Джинса. Для доказательства этого разложим функцию eh 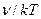 в ряд:
в ряд:
eh 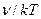 =1+
=1+ 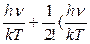 )
) 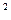 +
+ 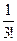 (
(  )
) 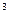 +… (16.21)
+… (16.21)
и, ограничившись первыми двумя членами разложения, из (16.19) получаем формулу Релея—Джинса (16.14):
R( 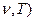 =
= 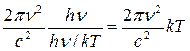 .
.
В предельном случае больших частот ( 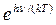 >>1) единицей в знаменателе формулы (16.19) можно пренебречь, тогда получим формулу
>>1) единицей в знаменателе формулы (16.19) можно пренебречь, тогда получим формулу
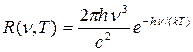 , (16.22)
, (16.22)
которая совпадает с выражением (16.12), т.е. с формулой Вина, причем, функция F(ν/Т) представляет собой выражение
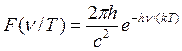 ,
,
которое действительно зависит от отношения частоты к температуре. График функции Вина показан на рис. 16.5. Функции Вина совпадает с формулой Планка только в области больших частот.
Интегральную излучательную способность АЧТ (закон Стефана—Больцмана) можно получить, проинтегрировав выражение (16.20) по длинам волн в интервале от 0 до 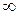 :
:
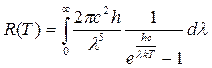 . (16.23)
. (16.23)
Произведем замену переменной. Обозначим 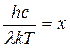 , тогда подстановка
, тогда подстановка 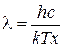 и
и 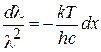 приводит выражение (16.21) к виду
приводит выражение (16.21) к виду
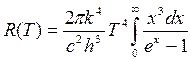 , (16.24)
, (16.24)
где 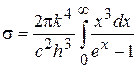 . Так как
. Так как 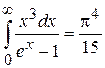 , то
, то
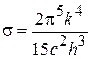 . (16.25)
. (16.25)
Как видим, величина s (постоянная Стефана-Больцмана) выражается через постоянные величины c, h, k.
Анологично, исследуя функцию (16.22) по переменной ν на экстремум, можно получить значение постоянной Вина, которая выражается также через постоянные с, h и k, и выполнить проверку закона смещения Вина.
Таким образом, формула Планка не только хорошо согласуется с
экспериментальными данными, но и содержит в себе частные законы теплового излучения. Следовательно, формула Планка является полным решением основной задачи теплового излучения, поставленной Кирхгофом. Ее решение стало возможным лишь благодаря революционной квантовой гипотезе Планка.
Дата добавления: 2017-10-04; просмотров: 4833;











