Фотонная теория света. Масса, энергия и импульс фотона.

В современной трактовке гипотеза квантов утверждает, что энергия ε колебаний атома или молекулы может быть равна hν, 2hν, 3hν и т.д., но не существует колебаний с энергией в промежутке между двумя последовательными целыми, кратными hν . Это означает, что энергия не непрерывна, как полагали на протяжении столетий, а квантуется, т.е. существует лишь в строго определенных дискретных порциях. Наименьшая порция hν называется квантом энергии. Гипотезу квантов можно сформулировать и как утверждение о том, что на атомно-молекулярном уровне колебания происходят не с любыми амплитудами. Допустимые значения амплитуды связаны с частотой колебания ν. В 1905 г. Эйнштейн выдвинул смелую идею, обобщавшую гипотезу квантов, и положил ее в основу новой теории света (квантовой теории фотоэффекта).

Для объяснения законов фотоэффекта А.Эйнштейн развил идеи Планка о квантовом характере теплового излучения. Он предположил, что свет не только излучается отдельными квантами, но и распространяется и поглощается веществом в виде квантов энергии. В связи с этим распространение электромагнитного излучения рассматривается уже не как непрерывный волновой процесс, а как поток дискретных квантов, движущихся в вакууме со скоростью света с. Эти кванты электромагнитного излучения были названы фотонами.

Фотоны как квазичастицы света обладают не только энергией 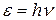, но и массой. Массу фотона можно определить с помощью выражения для энергии микрочастицы в релятивистской механике: .

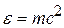Следовательно, масса фотона

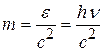. (17.2)

Введенное понятие массы фотона существенно отличается от понятия массы для обычных микрочастиц. Фотон не обладает массой покоя, т.е. для него 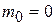. Если бы масса 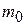фотона была отличной от нуля, то из формулы 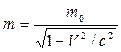для релятивистской массы при 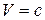мы получили бы, что 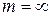, т.к. при 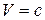знаменатель обращается в нуль. Отсюда следует, что масса 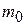фотона равна нулю.

Импульс фотона определяется выражением:

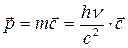. (17.3)

Тогда модуль импульса примет вид: 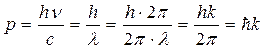, где

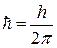где («аш» с чертой), k – волновое число. Поскольку волновой вектор 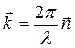направлен по направлению распространения световой волны, то он совпадает с направлением скорости света 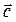и, следовательно, с направлением импульса 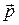. Таким образом, импульс 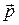может быть записан через волновой вектор 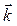, т.е.

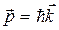. (17.4)

Наличие у фотона импульса экспериментально проявляется в том, что свет оказывает давление на тела. Формулу для светового давления можно получить, исходя из квантовых свойств света.

В соотношениях для энергии релятивистской частицы 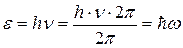и импульса 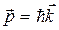заложена суть корпускулярно-волнового дуализма, так как, с одной стороны, корпускулярные свойства излучения характеризуются энергией 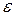и импульсом 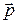, с другой стороны, волновые свойства излучения – частотой 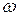и волновым вектором .

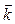Процесс поглощения света веществом сводится к тому, что фотоны передают всю свою энергию частицам этого вещества. С позиций квантовой природы света Эйнштейн дал наглядное объяснение явления фотоэффекта. Для того, чтобы вырвать электроны из вещества, необходимо совершить работу, которая называется работой выхода А. Эта работа расходуется на преодоление задерживающих сил, действующих в поверхностном слое металла. Если энергия 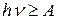, то фотоэффект будет наблюдаться. В соответствии с законом сохранения энергии Эйнштейн предложил уравнение:

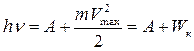. (17.5)

Здесь выражение 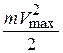= W_к представляет собой максимально возможную кинетическую энергию W_к электрона, вырываемого излучением частотой 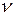. Так как работа выхода является константой для данного вещества, то кинетическая энергия электрона линейно зависит от частоты света и не зависит от его интенсивности (17.5).

Уравнение (17.5) объясняет все экспериментально установленные законы фотоэффекта: во-первых, из соотношения (17.5) следует, что максимальная скорость вырванных фотоэлектронов зависит не от интенсивности 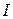, а от частоты 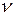света (второй закон фотоэффекта); во-вторых, внешний фотоэффект возможен только в том случае, если энергия фотона 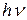больше или равна работе 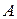выхода электрона из металла. Минимальная частота 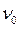, при которой еще возможен фотоэффект (третий закон фотоэффекта), определяется по формуле:

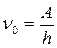. (17.6)

И, наконец, общее число 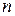фотоэлектронов, вылетающих из вещества за единицу времени, пропорционально числу фотонов, которые попадают за это же время на поверхность вещества, т.е. число 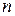пропорционально интенсивности падающего света (первый закон фотоэффекта).

С помощью соотношений (17.5) и (17.6) уравнение Эйнштейна для фотоэффекта (17.2) можно записать в виде

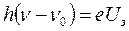. (17.7)

Если значения 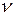и 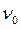известны, то, определив значение задерживающего напряжения 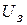, можно с помощью формулы (17.4) найти постоянную Планка

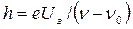. (17.8)

Можно также для известных значени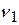й и 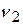измерить значения задерживающих напряжени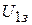й и 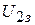и, используя уравнение Эйнштейна, рассчитать постоянную Планка, не определяя :

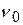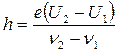. (17.9)

Совпадение экспериментальных значений по определению постоянной Планка 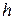согласно формулам (17.8) и (17.9) с результатами ее измерения в опытах по тепловому излучению абсолютно черного тела подтверждает справедливость уравнения Эйнштейна для фотоэффекта.