Вопрос 4. Основные законы релятивистской динамики. Закон взаимосвязи массы и энергии.
Эйнштейн показал, что существует зависимость инертной массы от скорости и это свойство всех материальных тел. Непостоянство массы тела – следствие постулатов теории относительности. Инертная масса движущихся релятивистских частиц зависит от величины их скорости, вернее, от отношения их скорости к скорости света:
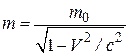 , (15. 10)
, (15. 10)
где m0 – масса покоя частицы, т.е. масса, измеренная в той инерциальной системе отсчета, относительно которой частица находится в покое; m - масса частицы в системе отсчета, относительно которой она движется со скоростью V. Следовательно, масса одной и той же частицы различна в разных инерциальных системах отсчета.
Как следует из (15.10), с увеличением скорости инерция тела (частицы) растет и при V→ с стремится к бесконечности. Значит ни одно тело при m > 0 не может достичь скорости с.
Опыты на ускорителях, где изучались движения быстрых заряженных частиц, скорость которых приближалась к скорости света, убедительно подтвердили зависимость массы от скорости и правильность формулы (15.10).
Из принципа относительности Эйнштейна, утверждающего инвариантность всех законов природы при переходе от одной инерциальной системы отсчета к другой, следует условие инвариантности уравнений физических законов относительно преобразований Лоренца. Основной закон динамики Ньютона
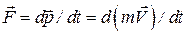
оказывается также инвариантным по отношению к преобразованиям Лоренца, если в нем справа стоит производная по времени от релятивистского импульса материальной точки, равного
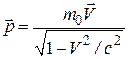 .
.
Основной закон релятивистской динамикиматериальной точки имеет вид
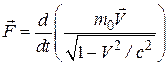 , (15.11)
, (15.11)
или
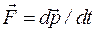 , (15.12)
, (15.12)
где
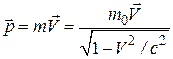 . (15.13)
. (15.13)
Уравнение (15.12) внешне совпадает с основным уравнением ньютоновской механики, но в (15.12) используется релятивистский импульс. Таким образом, уравнение (15.11) инвариантно по отношению к преобразованиям Лоренца и, следовательно, удовлетворяет принципу относительности Эйнштейна. Следует учитывать, что ни импульс, ни сила не являются инвариантными величинами. Более того, в общем случае ускорение не совпадает по направлению с силой. Сила совпадает с ускорением только в тех случаях, когда она нормальна к скорости или направлена по скорости.
В силу однородности пространства в релятивистской механике выполняется закон сохранения релятивистского импульса: релятивистский импульс замкнутой системы сохраняется, т.е. не изменяется с течением времени: 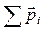 = const.
= const.
В теории относительности пространство и время органически связаны между собой и образуют единую форму существования материи – пространство-время. Положение материальной точки в теории относительности описывается четырехвектором 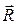 . 4-вектором в пространстве-времени считают всякую упорядоченную совокупность четырех чисел, представляющих собой определенные физические величины, чисел, которые изменяются при переходе от одной инерциальной системы к другой в соответствии с лоренцевыми преобразованиями.
. 4-вектором в пространстве-времени считают всякую упорядоченную совокупность четырех чисел, представляющих собой определенные физические величины, чисел, которые изменяются при переходе от одной инерциальной системы к другой в соответствии с лоренцевыми преобразованиями.
Основные определения кинематики и динамики материальной частицы в теории относительности с помощью 4-векторов можно записать следующим образом:
«положение» 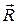 ,
,
«скорость» 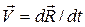 ,
,
«ускорение» 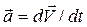 , (15.14)
, (15.14)
«импульс» 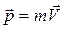 ,
,
«сила» 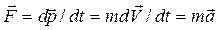 .
.
Как видно из приведенных выше формул, все эти определения по форме полностью соответствуют ньютоновой механике, только вместо 4-векторов следует подставить 3-вектора. Законы классической механики получаются как следствие теории относительности для предельного случая V<<с Классическая механика является некоторым приближением более точной релятивистской механики, которая базируется на постулате независимости скорости света от движения приемника и источника и постулате относительности.
Закон взаимосвязи массы и энергии.Поскольку массатела, как и кинетическая энергия, растет с увеличением скорости, следовательно, можно предполагать связь массы с кинетической энергией. Поэтому найдем кинетическую энергию релятивистской частицы.
Известно, что приращение кинетической энергии материальной точки на элементарном перемещении равно работе силы на этом перемещении:
dT = dA или 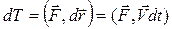 , (15.15)
, (15.15)
поскольку 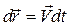 .
.
Из (15.12) получаем:
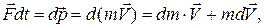
поэтому из (15.15) имеем:
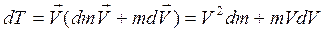 , (15.16)
, (15.16)
где учтено, что 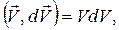 а
а 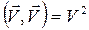 ,
,
Преобразуем выражение (15.10):
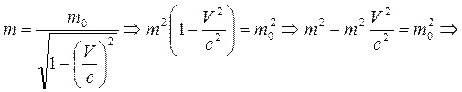
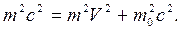 (15.17)
(15.17)
Найдем дифференциал этого выражения, учитывая, что 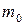 и с – константы:
и с – константы:
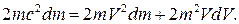
Разделив это выражение на число 2т, с учетом (15.16) получим:
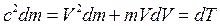 , т.е.
, т.е.
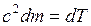 . (15.18)
. (15.18)
Выражение (15.18) показывает, что приращение кинетической энергии частицы пропорционально приращению ее массы.
Так как кинетическая энергия покоящейся частицы равна нулю, а ее масса равна массе покоя m0, то, интегрируя (15.18), получим
T = 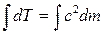 = (m - m0)с2, (15.19)
= (m - m0)с2, (15.19)
т.е. кинетическая энергия релятивистской частицы имеет вид:
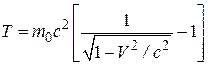 . (15.20)
. (15.20)
При 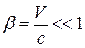 из выражения (15.20) получаем классическое значение энергии Т, учитывая формулу бинома Ньютона:
из выражения (15.20) получаем классическое значение энергии Т, учитывая формулу бинома Ньютона:
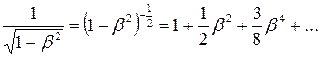
Ограничившись первыми двумя членами разложения в ряд, имеем:
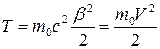 . (15.21)
. (15.21)
А. Эйнштейн обобщил положение (15.18), предположив, что оно справедливо не только для кинетической энергии частицы, но и для полной энергии частицы,
ΔЕ = с2Δm, (15.22)
т.е. если инертная масса увеличивается на некоторую величину Δm, то это означает увеличение энергии на с2Δm, и, наоборот, увеличение энергии на ΔЕ какого-либо физического объекта означает увеличение его инертной массы на ΔЕ/с2.
Из этого вывода Эйнштейн пришел к универсальной зависимости между полной энергией тела Е и его массой m:
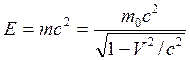 . (15.23)
. (15.23)
Уравнения (15.22) и (15.23) выражают фундаментальный закон природы − закон взаимосвязи (пропорциональности) массы и энергии: полная энергия системы равна произведению ее массы на квадрат скорости света в вакууме.
Величину m0с2 = Е0 называют энергией покоящегося тела. Тогда равенство (15.20) можно представить так:
Е = Е0 + Т, (15.24)
т.е. полная энергия равна сумме кинетической энергии Т и энергии покоя Е0. В полную энергию Е не входит потенциальная энергия тела во внешнем силовом поле. В классической механике энергию покоя не учитывают, считают, что при V = 0 энергия покоящегося тела равна нулю.
Отметим, что уравнение (15.23) имеет универсальный характер. Оно применимо ко всем видам энергии, например кинетической, потенциальной, электромагнитной и др., т.е. можно утверждать, что с энергией, какой бы формы она ни была, связана масса
m = Е/с2 (15.25)
и, наоборот, со всякой массой связана энергия. Еще в 1905 г. Эйнштейн на простом примере показал, что количество энергии электромагнитного излучения Е обладает инертной массой Е/с2. Иногда это называют эквивалентностью массы и энергии.
Чтобы охарактеризовать прочность связи и устойчивость системы каких-либо частиц (например, атомного ядра как системы протонов и нейтронов), вводят понятие энергии связи. Энергия связи системыравна работе, которую необходимо затратить, чтобы разложить эту систему на составные части (например, атомное ядро − на протоны и нейтроны). Энергия связи системы
Есв = ∑m0iс2 – M0с2, (15.26)
где m0i – масса покоя i –й частицы в свободном состоянии, M0 – масса покоя системы, состоящей из n частиц.
Закон взаимосвязи (пропорциональности) массы и энергии блестяще подтвержден экспериментом по определению энергии, выделяющейся при протекании ядерных реакций. Он широко используется для расчета энергетических эффектов при ядерных реакциях и превращениях элементарных частиц. Особенно показательно в этом отношении явление «аннигиляции» частиц (или «рождения» пары частиц), когда две частицы одинаковой массы, но с противоположными зарядами (например, электрон и позитрон) сталкиваются и их масса «превращается» в энергию электромагнитного излучения. Или лучше сказать так: в соответствии с законом сохранения энергии взаимодействующих частиц энергия перешла в такое количество энергии электромагнитного излучения, которое имеет массу, равную массе сталкивающихся частиц. Опыты атомной и ядерной физики не только подтвердили выводы теории относительности, но многие из них были поставлены на основе выводов этой теории.
Вернемся еще к энергии покоя Е0, о которой дорелятивистская физика не имела представления. Нагретое тело должно иметь большую массу, чем то же тело, но холодное; сжатая пружина имеет большую массу; вещества, химически прореагировавшие с выделением энергии, будут иметь меньшую массу, и т.п. Но практически такие изменения массы никогда не наблюдались вследствие очень малых относительных изменений массы – величина ΔЕ/с2 (где ΔЕ – приращение энергии) обычно ничтожно мала относительно массы m тел. Точность современных измерений недостаточна для определения таких изменений.
Связь между энергией и импульсом.Запишем выражения для энергии и импульса: 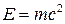 и
и 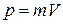 , тогда
, тогда
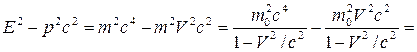
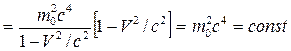 . (15.27)
. (15.27)
Величина 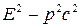 является инвариантной, т.е. имеет одно и то же значение в разных системах отсчета.
является инвариантной, т.е. имеет одно и то же значение в разных системах отсчета.
Подставим в (15.27) значение 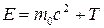 . Тогда
. Тогда 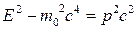 , т.е.
, т.е. 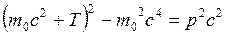 →
→ 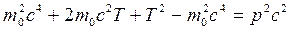 →
→
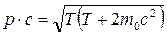 . (15.28)
. (15.28)
Из (15.28) при 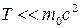 получаем выражение для классического импульса:
получаем выражение для классического импульса:
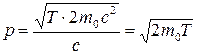 ,
,
а при 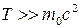 получаем выражение для ралятивистского импульса:
получаем выражение для ралятивистского импульса:
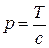 .
.
Дата добавления: 2017-10-04; просмотров: 3442;











