Вопрос 3. Преобразования Лоренца.

<43 44 454647 48 49 >

Преобразования координат и времени при переходе от одной инерциальной системы отсчета к другой в классической механике находят отражение в преобразованиях Галилея, из которых следует абсолютный характер интервалов времени и расстояний между двумя любыми точками пространства (формулы записаны для случая, когда система К'движется относительно К со скоростью 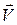вдоль оси Ох (рис. 15.1)):

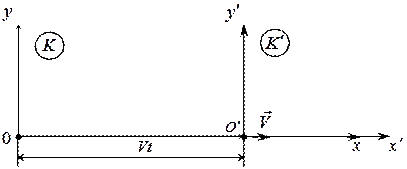
Рис.15.1

К → К' К' → К

x' = x – Vt x = x' + Vt (15.1)

y' = y y = y'

z' = z z = z'

t' = t t = t'.

В 1904 г., еще до появления теории относительности, Х. Лоренцем при анализе явлений электромагнетизма были предложены преобразования, относительно которых уравнения Максвелла инвариантны. Преобразования Лоренца для координат и времени при переходе от инерциальной системы К к системе К^′и наоборот имеют вид:

К → К' К' → К

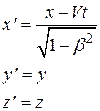
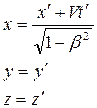(15.2)

, ,

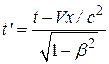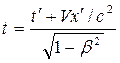где β = V/с.

Уравнения преобразований симметричны и отличаются лишь знаком при V. Из преобразований Лоренца вытекает, что при малых скоростях, т.е. при β<<1, они переходят в классические преобразования Галилея, которые являются, следовательно, предельным случаем преобразований Лоренца. Если предположить, что V > с, то выражения (15.2) для х, t, x', t' теряют физический смысл (становятся мнимыми). Это находится в соответствии с тем, что скорость света в вакууме является предельной скоростью движения.

Эйнштейн показал, что в теории относительности классические преобразования Галилея заменяются преобразованиями Лоренца, удовлетворяющими принципам относительности и инвариантности скорости света.

Из преобразований Лоренца следует важные выводы.

Во-первых, как расстояние, так и промежуток времени между двумя событиями меняются при переходе от одной инерциальной системы к другой, в то время как в рамках преобразований Галилея эти величины считаются абсолютными, не изменяющимися при переходе от системы к системе.

Во-вторых, как пространственные, так и временные преобразования (15.2) не являются независимыми, поскольку в закон преобразования координат входит время, а в закон преобразования времени – пространственные координаты, т.е. устанавливается взаимосвязь пространства и времени. Таким образом, теория Эйнштейна оперирует не с трехмерным пространством, к которому присоединяется понятие времени, а рассматривает неразрывно связанные пространственные и временные координаты, образующие четырехмерное пространство-время.

<43 44 454647 48 49 >

Дата добавления: 2017-10-04; просмотров: 1111;