ДВУХПАРАМЕТРИЧЕСКИЙ ЗАКОН РАСПРЕДЕЛЕНИЯ

Валоди Вейбулл (Waloddi Weibull)–1887-1979 - шведский ученый, исследователь в области усталости материалов, теории вероятностей и статистики обобщил два предыдущих закона, предложив показатель степени времени t сделать переменной величиной – параметром b.

Выражение закона Вейбулла для ВБР имеет вид

р(t) = Exp(-аt^b),(3-9)

где аи b - константы, называемые параметрами распределения.

При значении параметра b=1получаем выражение экспоненциального закона распределения, а при b=2 - закона Рэлея. Закон распределения Вейбулла называется обощенным потому, что включает в себя эти два закона в качестве частных случаев.

Плотность распределения

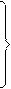f(t) = q¢(t) = [1-Exp(-аt^b)]¢ =

(3-10)

= (-а)bt^b-1[-Exp(-аt^b)] = аbt^b-1Exp(-аt^b)

Интенсивность отказов имеет вид

l(t) = аbt^b-1Exp(-аt^b)/Exp(-аt^b) = а b t^b-1.(3-11)

Рассмотрим влияние параметров bна вид зависимостей от времени интенсивности отказов. Подставляя в (3-11) b=1, получим l(t)=а=Const, а приb=2 - l(t)=2аt, то есть уравнения прямых линий. Взяв в качестве b < 1, значение 0.5, получим l(t)=

= 0.5/√t, графиком чего будет кривая, похожая на гиперболу. При 1<b<2, например, b=1.5, получим l(t)=1.5аt^0.5. Эта кривая соответствует функции квадратного корня. И, наконец, при b>2, например, b = 3, получаем l(t)=3аt², графиком чего является квадратичная парабола. Графики зависимостей l(t)при всех возможных вариантах параметра b представлены на рисунке 3.1.

Параметр bявляется коэффициентом формы кривых l(t) ир(t).

Вид зависимостейр(t) меняется не столь резко, как l(t), так как согласно общей формуле ВБР она является показательной функцией независимо от закона распределения (рис. 3.2). При b < 1 график р(t) похож на график экспоненты (b=1). При всех b>1 эта кривая имеет точку перегиба, причем резкость изгиба графика р(t) (изогнутость) увеличивается с ростом b.

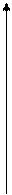
l(t) b=2 (закон Рэлея)

b=1 (эксп. з-н)

1<b<2

b<1 b>2

0 t

Рис. 3.1.