Построение изображений предметов с помощью тонкой линзы.

Вопрос 1. Преломление и отражение света на сферических поверхностях.

Сферические преломляющие поверхности часто встречаются в практике. Они ограничивают оптические стекла (линзы) – основные детали оптических приборов.

Предположим, что две прозрачные однородные среды с показателями преломления n₁ и n₂ разделяются сферической поверхностью с радиусом r. Введем понятие главная оптическая ось, под которой будем подразумевать прямую, проходящую через источник света (точка А₁) и центр кривизны (точка С) преломляющей поверхности ВD, (рис.6.1).

Рассмотрим, как преломляются оптические лучи, падающие из источника света на поверхность раздела двух сред.

Для определения значений углов и длин направленных отрезков воспользуемся следующим правилом. Расстояния будем считать

Рис.6.1.

положительными, если они отложены от точки О в направлении распространения светового луча, и отрицательными, если они отложены в сторону, противоположную световому лучу, рис.6.1.

Значения всех углов отсчитываются от направления оптической оси или нормали к поверхности ВD, причем углы, откладываемые по ходу часовой стрелки, считаются положительными, в обратном направлении - отрицательными.

Предполагаем, что пучок лучей очень узкий и образует очень малые углы с оптической осью или нормалями к разделяющим поверхностям. Такой пучок лучей называется параксиальным. В этом случае можно приближенно заменять синусы и тангенсы значениями этих углов в радианах.

Получим выражение для сферической преломляющей поверхности.

Из рис.6.1 видно, что площадь треугольника А₁LА₂ равна сумме площадей треугольников А₁LС и LА₂С, т.е.

пл. 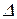А₁LС + пл. 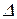LА₂С = пл. 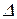А₁LА₂.

Обозначим длины сторон А₁L и LА₂ через S₁ и S₂ соответственно. Так как S₁<0, S₂>0, то для этих площадей можно записать:

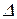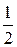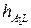пл. А₁LС = А₁L · , где 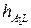- высота треугольника А₁LС, проведенная из вершины С на продолжение стороны А₁L (на рис.6.1 не показана); 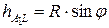, значит, пл. 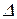А₁LС = 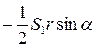(LС = r);

пл. 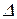С LА₂ = 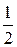А₂L · ,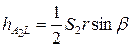

пл. 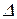А₁LА₂= 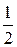А₁L· = .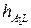

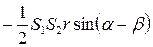Здесь высота 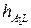проводится из вершины А₂ на продолжение стороны А₁L. Учтем, что .

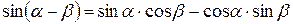Таким образом, окончательно имеем:

+ = .

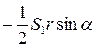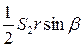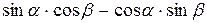Разделим выражение (1) на 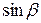, учитывая закон преломления, что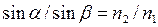

= .

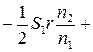
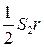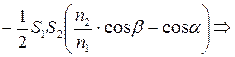
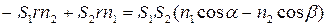Последнее выражение разделим на множитель :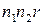

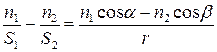. (6.1)

Положение точки А₂ зависит от угла наклона 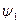падающего луча к оптической оси. Для параксиальных лучей углы 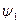, а также углы α и β малы. Для них можно принять, что 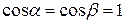, А₁L≈ А₁О = 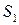, LА₂≈ОА₂= .

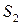В этом приближении формула (6.1) принимает вид:

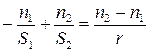, (6.1)

Величина

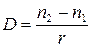, (6.2)

которая зависит только от показателей преломления сред и радиуса кривизны поверхности их раздела, называется оптической силой поверхности.

Выражение (6.1) с учетом (6.2)

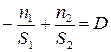(6.3)

является формулой для сферической преломляющей поверхности.

Из формулы (6.3) следует, что при заданных значениях оптической силы поверхности D, растояний S₁ и S₂ все параксиальные лучи, испускаемые точечным источником света А₁, сойдутся в одной точке А₂, т.е. преломляющая сферическая поверхность дает точечное (или стигматическое) изображение источника А₁. Если учитывать и непараксиальные лучи, то изображение точечного источника А₁ будет размытым.

Формула для сферической преломляющей поверхности показывает, что при прохождении лучей через оптическую систему в обратном направлении будет сформировано изображение, в точности совпадающее с исходным источником, т.е. если бы источник света был в точке А₂, то его изображение было бы в А₁ (взаимность). Выражение (6.3) охватывает все случаи преломления лучей на сферической поверхности. Используя установленное выше правило знаков для углов и длин направленных отрезков, можно рассмотреть случаи выпуклой (r > 0) и вогнутой (r < 0) поверхности.

Найдем место, где сойдутся параксиальные лучи от бесконечно удаленного источника А₁, рис.6.2 а. В этом случае учтем, что S₁ = - ∞, a S₂ ≡ f₂, и, подставив их в формулу (6.3), получим значение величины f₂, определяющей положение точки F₂, т.е. второго главного фокуса преломляющей поверхности:

n₂/ f₂ = (n₂ - n₁)/r,

откуда

f₂ = n₂ /D = r n₂/( n₂ – n₁). (6.4)

Определим положение первого главного фокуса F₁, поместив источник света А₁ на расстоянии S₂ = + ∞, т.е справа от поверхности BD, рис.6.2б. Для f₁ = S₁ при S₂ = ∞ получим

f₁ = - r n₁/( n₂ – n₁). (6.5)

Используя формулы (6.4) и (6.5), определим отношение главных фокусных расстояний:

f₂ / f₁ = - n₂ / n₁.

Рис.6.2.

Преобразуем формулу для сферической преломляющей поверхности (6.3), введя в нее значения главных фокусных расстояний. Разделим ее левую и правую части на значение оптической силы D преломляющей поверхности (6.1) и учтем соотношения (6.4) и (6.5):

r n₂/ S₂( n₂ – n₁) - r n₁/ S₁( n₂ – n₁) = 1 → f₂/S₂ + f₁/S₁ = 1. (6.6)

Из формул (6.4) – (6.6) для преломления света на сферической поверхности можно получить формулу для отражения света в сферическом зеркале, если в этих соотношениях положить n₂ = – n₁ (так как углы меняют знак), тогда получим

f₂ = f₁ = r/2 (6.7)

и 1/S₁ + 1/S₂ = 2/r. (6.8)

(6.8)– формула для отражения света в сферическом зеркале.