Влияние примесей неконденсирующихся газов
Наличие в паре неконденсирующегося газа затрудняет доступ пара к поверхности конденсации. В результате скорость конденсации уменьшается. Будем полагать, что стенка непроницаема. Ее температура tс ниже температуры основной массы парогазовой смеси tп0. По стенке течет пленка образовавшегося конденсата.
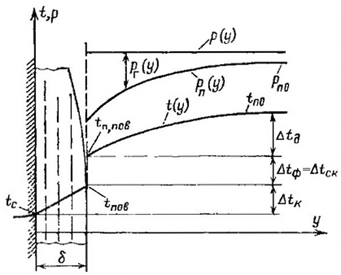
Распределение концентраций и температуры при конденсации пара из парогазовой смеси
Общее количество теплоты, передаваемой поверхности пленки, равно:
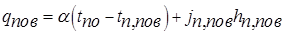
| (14.1) |
где 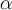 —коэффициент теплоотдачи от парогазовой смеси к пленке конденсата. Пар, достигший поверхности раздела фаз, конденсируется. При этом выделяется теплота фазового перехода
—коэффициент теплоотдачи от парогазовой смеси к пленке конденсата. Пар, достигший поверхности раздела фаз, конденсируется. При этом выделяется теплота фазового перехода
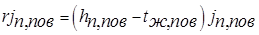
| (14.2) |
Теплота фазового перехода вместе с теплом, переданным конвективной теплоотдачей, переносится к твердой стенке, на которой находится конденсированная фаза. Перенос теплоты через движущуюся пленку конденсата определяется конвективным теплообменом, описанным ранее (Лекция №13). Твердой стенке передается и некоторая теплота переохлаждения конденсата относительно tпов так как температура по толщине пленки изменяется от tпов до tc. Большей частью теплота переохлаждения конденсата невелика и во многих расчетах ею можно пренебречь. Тогда при стационарном режиме плотность теплового потока можно считать неизменной по толщине слоя конденсированной фазы. Пренебрегая переохлаждением конденсата, плотность теплового потока на стенке можно описать следующим уравнением:
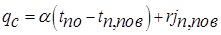
| (14.3) |
При расчете qc часто используют уравнение
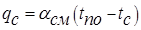 , ,
| (14.4) |
где 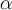 см — коэффициент теплоотдачи, отнесенный к разности температур стенки и пара (парогазовой смеси) вдали от поверхности конденсации.
см — коэффициент теплоотдачи, отнесенный к разности температур стенки и пара (парогазовой смеси) вдали от поверхности конденсации.
Коэффициент теплоотдачи 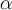 см является сложной величиной, учитывающей различные термические сопротивления. Суммарное термическое сопротивление
см является сложной величиной, учитывающей различные термические сопротивления. Суммарное термическое сопротивление
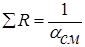
| (14.5) |
можно расчленить на термическое сопротивление конденсата Rk; термическое сопротивление фазового перехода Rф и термическое сопротивление подвода теплоты (пара) к поверхности конденсации (диффузионное термическое сопротивление) Rд
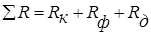 . .
| (14.6) |
Этим термическим сопротивлениям соответствуют температурные разности Δtk, Δtф и Δtд (смотри рисунок выше), причем
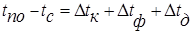 . .
| (14.7) |
Тогда для расчета qc получают уравнение
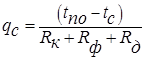 . .
| (14.8) |
Во многих задачах Rф много меньше, чем Rk и Rд, что позволяет пренебречь термическим сопротивлением фазового перехода (т.е. полагать tп,пов=tж,пов). Пренебрегая скачком температур Δtф, температуру поверхности конденсата tпов (tж,пов) можно рассматривать, как температуру насыщения пара при давлении насыщения pп,пов.
Тогда
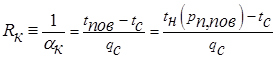 . .
| (14.9) |
Значения Rk или 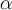 k могут быть определены по формулам, приведенным для конденсации сухого насыщенного пара на поверхности жидкости. Диффузионное термическое сопротивление определяется как:
k могут быть определены по формулам, приведенным для конденсации сухого насыщенного пара на поверхности жидкости. Диффузионное термическое сопротивление определяется как:
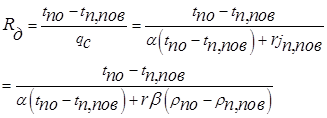
| (14.10) |
Коэффициент теплоотдачи 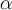 должен быть определен с учетом сопутствующего процесса массообмена. Из уравнения следует, что коэффициент теплоотдачи
должен быть определен с учетом сопутствующего процесса массообмена. Из уравнения следует, что коэффициент теплоотдачи 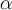 см зависит от интенсивности взаимосвязанных процессов тепло- и массообмена в парогазовой смеси и в пленке. Для расчета коэффициента
см зависит от интенсивности взаимосвязанных процессов тепло- и массообмена в парогазовой смеси и в пленке. Для расчета коэффициента 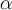 см необходимо предварительно определить коэффициент массоотдачи β. Средний коэффициент массоотдачи при пленочной и капельной конденсации пара на горизонтальной трубе из паровоздушной смеси, практически неподвижной на большом удалении от трубки, может быть определен по формуле
см необходимо предварительно определить коэффициент массоотдачи β. Средний коэффициент массоотдачи при пленочной и капельной конденсации пара на горизонтальной трубе из паровоздушной смеси, практически неподвижной на большом удалении от трубки, может быть определен по формуле
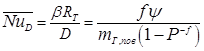 , ,
| (14.11) |
где
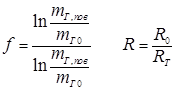 . .
| (14.12) |
Rт - радиус трубки (поверхности конденсата); R0 — радиус, при котором берется концентрация газа на удалении mг0. Индекс «пов» соответствует поверхности конденсата. Формула получена применительно к условиям, когда при фиксированном значении R0 много больше, чем Rт параметры парогазовой смеси однородны. Формулой учитываются как стефанов поток, так и свободная конвекция.
При
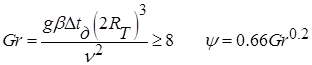 . .
| (14.13) |
При Gr≤8 можно принять ψ=1 (свободная конвекция не влияет). В формулу подставляются физические параметры парогазовой смеси, взятые по температуре tп0. Практически важной задачей является процесс тепломассообмена при пленочной конденсации пара из движущейся паровоздушной смеси на горизонтальных одиночных трубах и трубах, собранных в пучок. Тепло- и массоотдача при названных условиях исследовались в ряде работ. В опытах паровоздушная смесь поступала к одиночной горизонтальной трубе и пучку горизонтальных труб сверху. Давление паровоздушной смеси р изменялось от 0,0627 до 0,089МПа; начальное содержание воздуха в водяном паре εг0=pг0/p=0,01÷0,56. Получено, что средний коэффициент массоотдачи определенного ряда труб при Re=350÷4800 может быть рассчитан по уравнению:
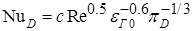 , ,
| (14.14) |
где для одиночной трубы с=0,47, для первого рада пучка с=0,53, для третьего и последующих рядов с=0,82. Здесь
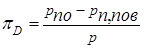 . .
| (14.15) |
Ниже на рисунке данные, полученные по формуле для одиночной трубы сопоставлены с опытными данными.
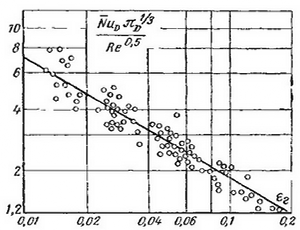
|
| <== предыдущая лекция | | | следующая лекция ==> |
| Универсальная аппроксимация для расчета теплообмена при конденсации | | | Законы излучения абсолютно черного тела. |
Дата добавления: 2017-10-04; просмотров: 2220;

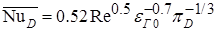 .
.
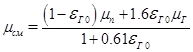 .
.
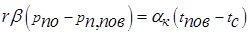 .
.










