Законы излучения абсолютно черного тела.
Излучение. Основные понятия и законы
Количественные характеристики излучения
Тепловое излучение тел - это электромагнитное излучение, определяемое температурой.При температурах 273 К - 4000 К тепловое излучение занимает интервал длин волн примерно от 1000 мкм до 0,7 мкм, то есть включает инфракрасное излучение - от дальнего миллиметрового диапазона вплоть до красного участка видимого света. Видимый свет (длина волны 0,4 - 0,7 мкм ) является тепловым излучением поверхности Солнца с температурой примерно 6000 К. Таким образом, если мы скажем, что тепловое излучение - это инфракрасное излучение, то это будет правильным для тех температур, с которыми мы имеем дело в обычной технике.
Большинство технических твердых материалов непрозрачно для инфракрасного излучения (даже стекло). Это означает, что поглощение и излучение происходит на поверхности тел и определяется температурой поверхности и ее состоянием (шероховатостью, степенью окисленности и т.п.). Твердые (плотные) тела имеют непрерывный спектр.
Излучение и поглощение газов (разреженных сред) имеет существенные особенности. Одноатомные и двухатомные газы ( такие как азот, кислород ) практически прозрачны для инфракрасного излучения. Трехатомные газы (для нас особенно важны водяной пар и углекислый газ, содержащиеся в продуктах сгорания) сильно поглощают и излучают, но только на определенных длинах волн. Их спектр имеет полосовой характер. Вторая важная особенность - объемный характер излучения: малый объем газа или газ при очень малом давлении содержит малое число излучающих и поглощающих молекул и поэтому слабо излучает и практически прозрачен, и наоборот, большие объемы при большом давлении сильно излучают и поглощают ( в своих полосах спектра).
Основные понятия и законы
Плотностью потока излучения E, Вт/м2, называют поток энергии (Дж/c=Вт), излучаемый с единицы поверхности (м2) по всем направлениям внутрь контрольной полусферы (рисунок ниже):
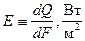 . .
| (15.1) |
Это интегральное излучение, просуммированное по всем длинам волн.
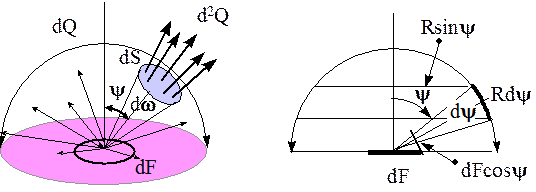
К определению понятий плотности потока и энергетической яркости излучения.
Если рассмотреть некоторый малый интервал длин волн от 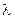 до
до 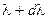 , измерить плотность потока излучения в этом интервале dE, Вт/ м2 , и отнести этот поток к единичному интервалу длин волн, то получится спектральная плотность потока излучения:
, измерить плотность потока излучения в этом интервале dE, Вт/ м2 , и отнести этот поток к единичному интервалу длин волн, то получится спектральная плотность потока излучения:
 . .
| (15.2) |
Эта величина показывает, как сильно излучает тело на той или иной волне. Используя световую аналогию, можно сказать, что спектральная плотность определяет цвет излучения.
Энергетическая яркость L определяется соотношением:
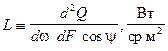 , ,
| (15.3) |
где 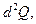 Вт - поток энергии, излучаемой площадкой dF, м2 , внутри телесного угла
Вт - поток энергии, излучаемой площадкой dF, м2 , внутри телесного угла 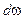 , стерадиан, в направлении, составляющем угол
, стерадиан, в направлении, составляющем угол 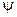 с нормалью (рисунок выше).
с нормалью (рисунок выше).
Энергетическая яркость показывает, как сильно излучает тело в заданном направлении. Это очень важная характеристика, поскольку в дальнейшем нам придется рассчитывать излучение данной поверхности на другие тела, произвольно расположенные в пространстве. Полезно пояснить само происхождение термина «яркость». Оно обязано световой аналогии и нашему зрительному восприятию. Если мы будем рассматривать святящуюся поверхность под разными углами, то видимой величиной поверхности будет 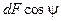 . И если плотность потока излучения, отнесенная к этой видимой поверхности, будет одинаковой, то предмет будет казаться нам одинаково ярким со всех направлений.
. И если плотность потока излучения, отнесенная к этой видимой поверхности, будет одинаковой, то предмет будет казаться нам одинаково ярким со всех направлений.
Самой простой была бы ситуации, когда энергетическая яркость не зависит от направления (угла 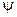 ). Их называют диффузными излучателями.
). Их называют диффузными излучателями.
В этом случае плотность потока E (по всем направлениям внутрь полусферы) связана с энергетической яркостью простым соотношением:  .
.
Следовательно, излучение в заданном направлении можно подсчитать как
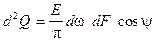 . .
| (15.4) |
Последнее соотношение называют законом Ламберта для диффузных излучателей.
Доказательство этой формулы простое и следует из определения величин:
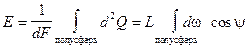 . (15.5) . (15.5)
|
Интегрирование производится по всем направлениям внутрь контрольной полусферы радиуса R. Яркость L выносится за знак интеграла как постоянная для диффузных поверхностей величина. Элементарный телесный угол заменяется, согласно определению, полоской на полусфере, отнесенной к квадрату радиуса (рисунок выше):
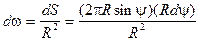 , (15.6) , (15.6)
|
так что интеграл по полусфере сводится к вычислению табличного интеграла:
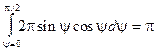 , откуда следует: , откуда следует: 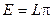 . (15.7) . (15.7)
|
Закон Кирхгофа
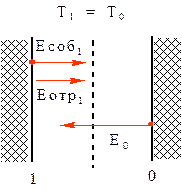
К формулировке закона Кирхгофа.
Рассмотрим состояние равновесия двух бесконечных плоскопараллельных пластин с одинаковой температурой. В такой системе все излучение одной пластины попадает на другую, а результирующий поток равен нулю.
Пусть одна из пластин - абсолютно черная. Условимся все величины, относящиеся к черному телу, снабжать индексом «0». Другая поверхность, с индексом «1» - реальная, с коэффициентом поглощения, меньшим единицы. Запишем для пластины 1 результирующее излучение, учитывая, что падающее на пластину 1 излучение - это собственное излучение черной пластины:
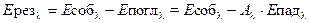 , ,
| (15.8) |
где 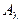 - спектральный коэффициент поглощения,
- спектральный коэффициент поглощения, 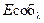 - спектральная плотность собственного потока излучения, и т.д.
- спектральная плотность собственного потока излучения, и т.д.
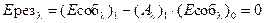 , ,
|
откуда и следует формулировка закона Кирхгофа:
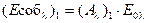 при одинаковой температуре тел!!! при одинаковой температуре тел!!!
| (15.9) |
Обозначение 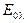 и
и 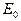 мы всегда будем использовать в дальнейшем соответственно для спектральной и интегральной плотности потока излучения абсолютно черного тела.
мы всегда будем использовать в дальнейшем соответственно для спектральной и интегральной плотности потока излучения абсолютно черного тела.
Это - замечательное соотношение, утверждающее, что черные тела не только абсолютные поглощатели излучения, но и абсолютные излучатели. Действительно, коэффициент поглощения другого тела не может быть больше единицы.
Отметим сразу еще одно важное свойство черных тел: черные тела являются диффузными излучателями. Для них всегда справедлив закон Ламберта.
Для реальных тел спектральный коэффициент поглощения является функцией температуры и, в той или иной степени, длины волны. Однако для большинства технических материалов можно считать коэффициент поглощения практически постоянным в достаточно широком диапазоне длин волн. Обобщением этого свойства является модель серого тела с постоянным (не зависящим от длины волны излучения) коэффициентом поглощения. Очевидно, что в этом случая значения спектрального и интегрального коэффициентов поглощения одинаковы: 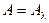 .
.
Для интегрального (проинтегрированного по всем длинам волн) излучения закон Кирхгофа записывается в виде:
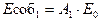 при одинаковой температуре тел!!! при одинаковой температуре тел!!!
| (15.10) |
Коэффициент поглощения существенно зависит от температуры.
Законы излучения абсолютно черного тела.
Закон Планка.
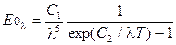 , (15.11) , (15.11)
|
где 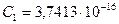 Вт м2 и
Вт м2 и 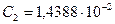 м К - абсолютные константы, составленные из скорости света, постоянных Больцмана и Планка.
м К - абсолютные константы, составленные из скорости света, постоянных Больцмана и Планка.
В результате получаютзакон смещения Вина:
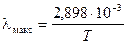 , м. , м.
| (15.12) |
Закон Планка - главный инструмент тех, кто занимается солнечной энергетикой. С помощью закона Планка астрофизики измеряют температуру звезд, сравнивая спектры их излучения с Планковским спектром и подбирая температуру так, чтобы они совпадали.
Дата добавления: 2017-10-04; просмотров: 1705;











