Потенциальная помехоустойчивость передачи непрерывных сообщений

Пусть передается непрерывное сообщение a(t), причём |a(t)| ≤ 1, а его мощность 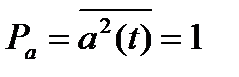; в общем случае a(t) можно представить в виде разложения 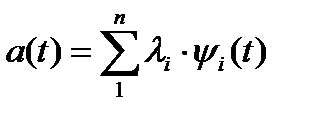по единичным ортогональным составляющим с коэффициентами l_i. Тогда сигнал S(t; a) = S(t; λ₁, λ₂, …λ_n) будет получать в процессе модуляции приращения в соответствии с модуляционным вектором определяющим 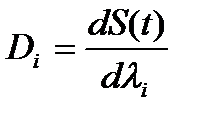свойства модулятора.

С другой стороны, принятый сигнал S*(t) за счет действующей в канале помехи ξ(t) будет отличаться от переданного S(t). Как следствие этого, коэффициенты λ_i = λ_i + Δ λ_i также будут отличаться от переданных λ_i. В результате будем иметь

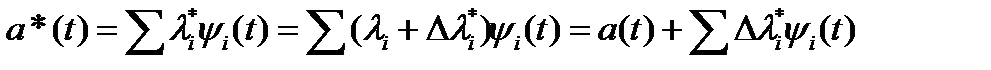, (18.15)

а для погрешности передачи получим .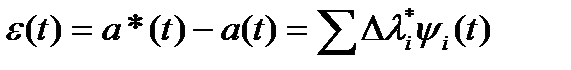

Оптимальный приемник Котельникова измеряет расстояние .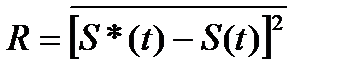

Минимальному значению R соответствуют приращения Δλ_i*, определяемые из условия 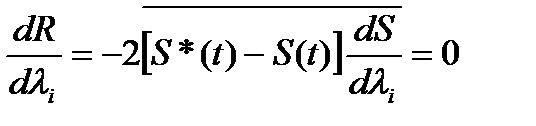, т.е.

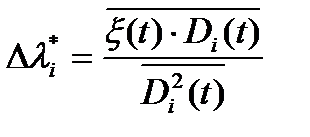. (18.16)

На основе (18.16) получаем выражение для средней мощности шума на выходе приемника 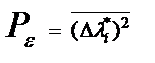. При слабых помехах ξ(t) спектральную мощность шума на выходе можно представить в виде

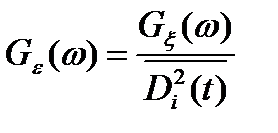, (18.17)

а P_ε – соответственно

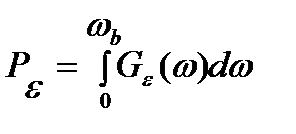. (18.18)

Составим отношение средних мощностей сообщения и шума на выходе приемника

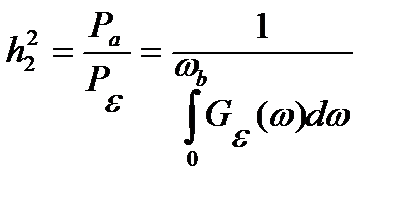. (18.19)

Выражения (18.18) и (18.19) используются для сравнительной оценки потенциальной помехоустойчивости различных видов модуляции. В результате анализа получены следующие выражения G_ε(ω) и h₂².

Амплитудная модуляция S(t) = A[1 + ma(t)]cos ω₀t

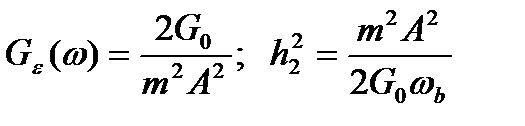. (18.20)

Фазовая модуляция S(t) = Acos[ω₀t + Δφ_ma(t)]

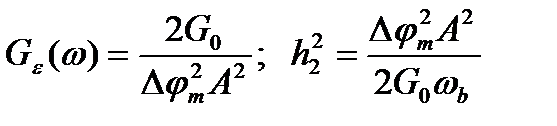. (18.21)

Частотная модуляция

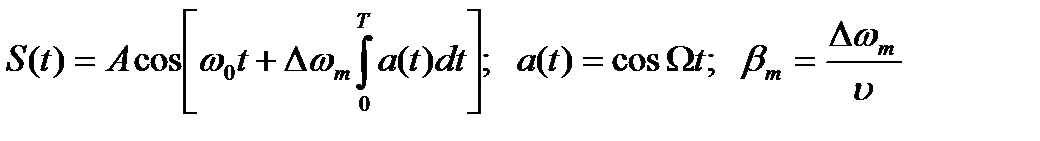
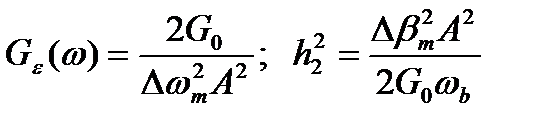. (18.22)

Из (18.20 – 18.22) следует, что при АМ (m = 1) помехоустойчивость можно увеличить лишь за счет увеличения мощности сигнала; при ФМ и ЧМ помехоустойчивость можно увеличить также путем увеличения индексов модуляции Δφ_m и b_w, что достигается за счет расширения спектра сигнала.

Все широкополосные системы модуляции обеспечивают высокую помехоустойчивость h₂² при условии, что отношение сигнал-помеха на входе h₁² больше некоторого порогового значения (рис. 18.5). При h₁² < h₁²_пор широкополосные системы теряют свои преимущества (резко снижается помехоустойчивость); возникающее при этом явление называют явлением порога помехоустойчивости.

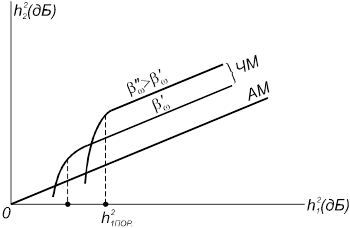
Рис. 18.5. Графики G_ε(ω) для АМ, ФМ и ЧМ в соответствии с 18.20 – 18.22