Адаптивный режекторный фильтр

В некоторых случаях входной сигнал представляет собой сумму составляющей сигнала и аддитивной синусоидальной помехи. Обычно для подавления такой помехи используется режекторный фильтр. В этом подразделе рассматривается реализация режекторного фильтра с помощью адаптивного устройства подавления помех. Преимущества такого режекторного фильтра заключаются в том, что он позволяет регулировать полосу частот и осуществлять адаптивное слежение за точным значением частоты и фазы помехи. Эти результаты распространяются и на случай, когда на эталонном входе имеется сигнал на многих частотах [14].

На рис. 19.3. приведена схема устройства подавления одночастотной помехи с двумя адаптивными весовыми коэффициентами. На вход устройства может подаваться сигнал любого вида – случайный, детерминированный, периодический, импульсный и т. д. – или любая комбинация этих сигналов. На эталонном входе действует чистый синусоидальный сигнал C∙cos(Ω₀t + φ). Отсчеты входных сигналов берутся с интервалами Т секунд. Здесь x_1k – отсчеты эталонного сигнала, а x_2k – отсчеты этого сигнала, сдвинутого по фазе на 90°.

Преимущества такого режекторного фильтра заключаются в том, что он позволяет регулировать полосу частот, формировать нули и осуществлять адаптивное слежение за точным значением частоты и фазы помехи.

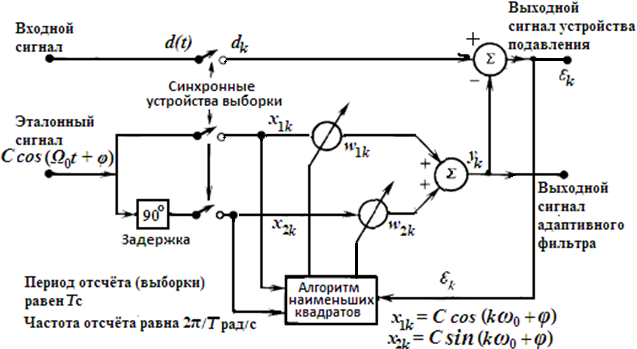
Рис. 19.3. Одночастотный адаптивный режекторный фильтр

Рассматривая прохождение сигнала от входа до выхода системы на рисунке 19.3. можно найти линейную передаточную функцию устройства подавления помех. При замкнутой петле обратной связи передаточная функция устройства подавления помех

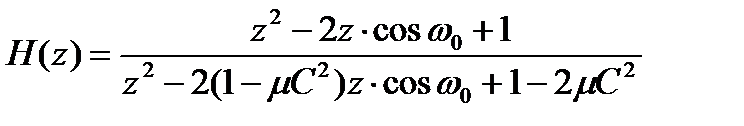. (19.19)

Из равенства (19.19) следует, что на частоте ω₀ эталонного сигнала устройство подавления одночастотной помехи обладает свойствами режекторного фильтра. Нули передаточной функции расположены на z-плоскости в точках

z = e^±jωo. (19.20)

т. е. точно на окружности единичного радиуса под углами ±ω₀ радиан.

Полюса передаточной функции расположены в точках

z = (1- μC²)∙cosω₀ ± j[(1 - 2μC²) - (1 - 2μC²)²∙cos²ω₀]^1/2, (19.21)

т. е. внутри окружности единичного радиуса на расстоянии от начала координат (1 - 2μC²)^1/2, приближенно равном 1 - 2μC², и под углами

±cos^-1[(1 - μC²) (1 - 2μC²)^-1/2cos ω₀]. (19.22)

При медленной адаптации (т. е. при небольших значениях μC²) эти углы определяются множителем, которым приблизительно равен 1.

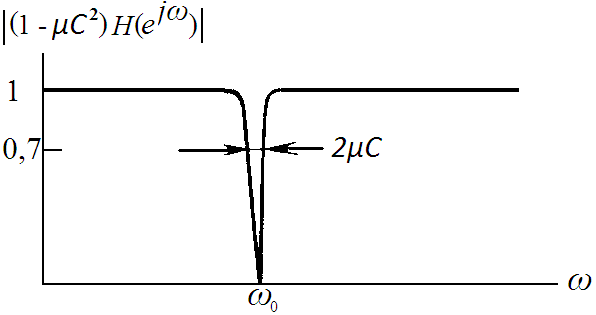
Рис. 19.4. Передаточная функция одночастотного адаптивного устройства подавления помех

Основной вывод состоит в том, что в практических случаях углы полюсов и нулей почти равны.

На рис. 19.4 показано расположение полюсов, нулей и точек половинной мощности передаточной функции. Поскольку нули лежат на окружности единичного радиуса, глубина режекции в децибелах для передаточной функции на частоте ω_о равна бесконечности.

Форма провала АЧХ определяется расстоянием, которое приблизительно равно μС². Длина дуги окружности единичного радиуса, заключенной между точками половинной мощности, соответствует полосе режекции фильтра и равна

BW = 2μС² рад = μС²/πT Гц. (19.23)

Форма АЧХ в полосе режекции обычно определяется добротностью Q, представляющей собой отношение центральной частоты к ширине полосы режекции:

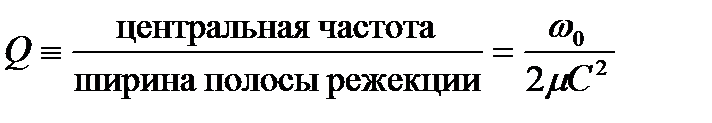. (19.24)

Таким образом, устройство подавления одночастотной помехи при синусоидальном эталонном сигнале эквивалентно устойчивому режекторному фильтру. В общем случае глубина режекции адаптивного устройства выше, поскольку в результате адаптивного процесса даже при медленном изменении частоты эталонного сигнала поддерживается правильное для подавления соотношение фаз.