ВОЗДУШНЫЕ ЛИНИИ ЭЛЕКТРОПЕРЕДАЧИ

СХЕМЫ ЗАМЕЩЕНИЯ ЛИНИЙ ЭЛЕКТРОПЕРЕДАЧИ

Принципиально расчёты электрических сетей базируются на тех же законах, что и расчёты любой иной цепи переменного тока. Однако специфика электрических сетей в энергетических системах такова, что непосредственное использование приёмов расчёта электрических цепей, известных из электротехники, является весьма затруднительным.

Следовательно, возникает объективная необходимость применить замещение реальных электрических сетей их расчётными схемами. В схемах замещения как собственно линии электропередачи, так и трансформаторы (автотрансформаторы) заменяют набором активных и реактивных сопротивлений и проводимостей. Величины этих сопротивлений и проводимостей, очевидно, должны быть такими, чтобы обеспечивать достоверные результаты расчёта режимов электрических сетей и систем.

Кроме того, введение любого элемента в схему замещения должно быть убедительно обосновано, исходя из физических процессов, сопровождающих передачу и преобразование электрической энергии. Наряду с очевидным различием между линиями электропередачи, предназначенными лишь для транспортировки электроэнергии, и трансформаторами, которые помимо передачи электроэнергии ещё обеспечивают преобразование её параметров, можно обнаружить достаточно признаков, общих для обеих категорий. Это последнее обстоятельство в известной степени обеспечивает унифицированный подход при замещении в расчётных схемах электрических сетей как собственно линий электропередачи, так и трансформаторов (автотрансформаторов), являющихся непременными звеньями на пути транспортировки электроэнергии от её производителя к потребителю.

В большинстве случаев можно полагать, что параметры линии электропередачи или, иными словами, активные и реактивные сопротивления и проводимости равномерно распределены по её длине. Для линии сравнительно небольшой длины распределённость параметров можно не учитывать и использовать сосредоточенные параметры: активное r_л и реактивное х_л сопротивления линии, активную g_л и реактивную b_л – проводимости линии.

ВОЗДУШНЫЕ ЛИНИИ ЭЛЕКТРОПЕРЕДАЧИ

Воздушные линии электропередачи напряжением 110 кВ и выше при длине до 300 - 400 км обычно представляются П-образной схемой замещения (рис. 2.1).

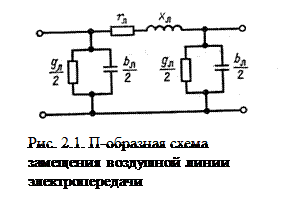
Активное сопротивление определяется по формуле

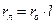, (2.1)

где r_о – удельное сопротивление, Ом/км (при температуре провода +20^оС);

l – длина линии, км.

Для электрических сетей, выполненных из цветного металла, при частоте f_с = 50 Гц влияние поверхностного эффекта очень незначительно. Поэтому в расчётах таких сетей активное сопротивление проводов принимают равным их омическому сопротивлению (или сопротивлению постоянному току).

Определение активного сопротивления стальных проводов, применяемых для сетей переменного тока, поскольку эти провода представляют собою ферромагнитный материал, отличается от расчётов сопротивления проводов из цветного металла.

Активное удельное сопротивление для сталеалюминиевых проводов определяется по таблицам в зависимости от поперечного сечения. При температуре провода, отличной от +20°С, сопротивление линии уточняется по известным из курса “Электротехнические материалы” формулам.

Реактивное сопротивление определяется следующим образом

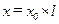где x₀ – удельное реактивное сопротивление, Ом/км.

Это сопротивление обусловлено переменным магнитным полем, возникающим вокруг проводов линии электропередачи при протекании по ним переменного тока.

Чем больше расстояние между проводами и меньше диаметр провода, тем больше индуктивное сопротивление линии.

Удельные индуктивные сопротивления фаз воздушной линии в общем случае различны. При расчетах симметричных режимов используют среднее значение x₀:

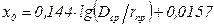[Ом / км], (2.2)

где r_пр – радиус провода;

D_ср – среднегеометрическое расстояние между фазами, определяемое соотношением

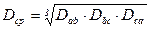, (2.3)

где D_ab; D_bc; D_ca – расстояния между проводами соответствующих фаз “a”, “b”, “с”.

Для наиболее распространенных способов расположения фаз характерно одно из двух (рис. 2.2) их размещений.

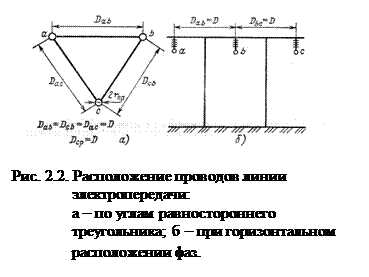При размещении параллельных цепей на двухцепных опорах потокосцепление каждого фазного провода определяется токами обеих цепей. Отличие х_о одной цепи при учёте и не учете влияния другой цепи не превышает 6 % и не учитывается при практических расчётах.

В ЛЭП при U_н ≥ 330 кВ провод каждой фазы расщепляется на несколько проводов, что соответствует увеличению эквивалентного радиуса провода.

В выражении (2.2) вместо r_пр используется

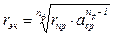, (2.4)

где r_эк – эквивалентный радиус провода;

а_ср – среднеарифметическое расстояние между проводами одной фазы;

n_ф – число проводов в одной фазе.

Для линии с расщеплёнными проводами последнее слагаемое в (2.2) уменьшается в “n_ф” раз, т.е. имеет вид 0,0157/ n_ф.

Активное удельное сопротивление расщеплённой фазы определяется так:

r_o = r_o_,пр/ n_ф,

где r_o_,пр – удельное сопротивление провода данного сечения, определённое по справочным таблицам.

Для сталеалюминиевых проводов х_о определяется по справочным таблицам в зависимости от сечения, для стальных – в зависимости от сечения и тока.

Интересно отметить, что расщепление проводов фаз в России впервые было применено в пятидесятые годы на ЛЭП Самара – Москва, в каждой фазе которой подвешены три провода марки АСО – 480 с расстоянием между проводами 400 мм. Это позволило снизить индуктивное сопротивление приблизительно на (25-30)%.

Активная проводимость соответствует двум видам потерь мощности: от тока утечки через изоляторы и на корону.

Токи утечки через изоляторы малы и потерями мощности в них можно пренебречь.

Явление короны заключается в том, что, если напряжённость электрического поля вокруг проводов вследствие приложенного к ним напряжения превышает величину электрической прочности воздуха, равную 21,2 кВ/см (2,12 кВ/мм) при температуре +25^оС, нормальных давлении и влажности, то вокруг проводов возникает ионизация воздуха, проявляющаяся в виде фиолетового свечения, характерного шипящего треска и сопровождающееся запахом озона.

Ионизация воздуха (явление короны) связано с потерями активной мощности. Напряжение, при котором возникают потери на корону, называются коронным или критическим напряжением короны.

Критическое фазное напряжение короны равно:

U_кр,ф = 48,9 · m_o · m_n × δ × r · lg 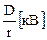, (2.5)

где m_o – коэффициент, учитывающий состояние поверхности провода; для одно-проволочных проводов m_o = 0,93…0,98, а для многопроволочных m_o = 0,83…0,87;

m_n – коэффициент, учитывающий состояние погоды; при сухой и ясной погоде m_n = 1; при плохой погоде (туман, иней, гололёд, дождь, снежная буря) m_n = 0,8;

δ = 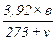- коэффициент, учитывающий атмосферное давление “в” 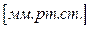и температуру воздуха υ 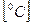; при в = 76 см. рт. ст. и υ = 25^оС коэффициент δ = 1;

r – наружный диаметр провода (см) (определяется по стандарту на провода);

D – расстояние между осями проводов (см).

Критическое междуфазное напряжение короны

U_кр = 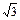· U_кр,ф (2.6)

Потери на корону наступают при совпадении напряжения линии с критическим напряжением короны и возрастают по мере увеличения напряжения сверх критического.

Поэтому для выяснения, будет ли в данной ЛЭП потеря мощности на корону, необходимо подсчитать величину критического напряжения короны и сравнить её с величиной рабочего напряжения линии U.

Из (2.5) следует, что наиболее радикальным средством снижения потерь мощности на корону (по существу, на исключение короны) является увеличение радиуса провода “r”. В связи с этим существуют нормативы, ограничивающие по минимуму сечение проводов: на 110 кВ – 70 мм²; на 150 кВ – 120 мм²; на 220 кВ – 240 мм² .

Как уже отмечалось, при U ≥ 330 кВ практикуется расщепление провода каждой фазы на несколько проводов, что соответствует увеличению эквивалентного радиуса провода.

Как следствие, согласно (2.5), этот приём вызывает увеличение напряжения короны и в соответствии с (2.7) приводит к уменьшению потерь мощности на корону. Эти потери имеют достаточно высокий уровень. В частности, для нерасщеплённых проводов на ВЛ 330 кВ потери достигают 2-4 кВт/км, а на ВЛ 750 кВ (даже при расщеплении фазы на пять проводов) уровень потерь на корону 9-16 кВт/км.

Что касается расстояния между проводами “D”, то, входя под знак логарифма, оно влияет на коронное напряжение незначительно. Физически это объясняется тем, что при увеличении диаметра провода плотность электрического поля у поверхности провода уменьшается в гораздо большей степени, чем от увеличения расстояния между проводами.

К тому же увеличение расстояния между проводами значительно повышает стоимость ЛЭП и для снижения потерь на корону не применяется.

Величина потерь активной мощности на корону во всех трёх фазах при напряжении U с частотой f_c = 50 Гц определяется по эмпирической формуле

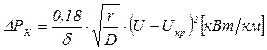. (2.7)

Активная проводимость, отнесённая к 1км длины линии, может быть найдена из выражения

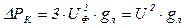, (2.8а)

т.е. 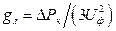(2.8б)

или

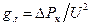. (2.8в)

Формулы (2.5) и (2.7) для определения U_кр,ф и DР_к справедливы для ЛЭП с расположением проводов трёхфазной линии в вершинах равностороннего треугольника.

При расположении проводов в одной плоскости корона на среднем проводе наступает при напряжении на 4% меньшем, а на крайних - на 6% большем, чем U_кр, подсчитанное по (2.5) для расположения проводов в вершинах равностороннего треугольника. Явление короны недопустимо в ЛЭП не только из-за потерь мощности, которые при определённых условиях могут достигать ощутимых значений, но и из-за вызываемых этим явлением коррозии проводов, радиопомех и вредного влияния на провода связи (здесь можно предположить и наличие проводной связи с использованием проводов самой ЛЭП, полагая, в частности, диспетчерскую связь через провода ЛЭП).

В практике проектирования электрических сетей с U ≤ 220 кВ потери на корону не учитываются. В сетях с U > 330 кВ определение потерь мощности при расчёте оптимальных режимов включает в себя и расчёт потерь на корону.

Ёмкостная проводимость линии обусловлена наличием частичных емкостей у каждого из проводов линии как к другим проводам, так и к земле (рис. 2.3).

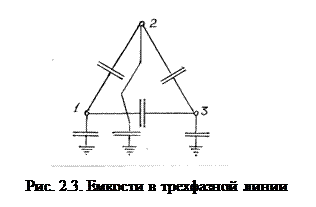Рабочая ёмкость провода составляется из частичных ёмкостей и представляет собой отношение всего количества электричества, соответствующего всем силовым линиям, исходящим от данного провода, к другим проводам и к земле, к потенциалу этого провода или, короче говоря, отношение заряда данного провода к его потенциалу. Понятие рабочей ёмкости справедливо лишь для симметричной системы, какой является трёхфазная ЛЭП с расположением проводов в вершинах равностороннего треугольника при достаточной удалённости проводов от земли.

В несимметричной трёхфазной ЛЭП понятием рабочей ёмкости можно пользоваться лишь при условии, что на линии осуществлён полный цикл транспозиции проводов. При этом влиянием на ёмкость земли, соседних проводов и тросов пренебрегают.

Эти допущения дают погрешность в определении рабочей ёмкости воздушных трёхфазных линий в наиболее неблагоприятном случае не более 5 %, что в большинстве случаев допустимо.

В практических расчётах ёмкость воздушной трехфазной линии определяется по формуле:

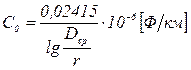, (2.9)

где D_ср и r – соответственно среднее расстояние между осями проводов и радиус провода.

Ёмкостная проводимость линии “b_л”, обусловленная ёмкостями между проводами разных фаз и ёмкостью провод-земля, определяется следующим образом

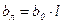где b₀ - удельная ёмкостная проводимость, См/км;

l – длина линии, км.

Величина “b₀” находится по справочным таблицам, либо по формуле

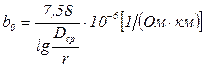. (2.10)

Наличие ёмкости проводов вызывает в линии ток, создаваемый приложенным к линии переменным напряжением и соответственно переменным электрическим полем, под влиянием которого происходит перемещение электрических зарядов. Этот ток называется емкостным или зарядным током линии.

Численно удельный ёмкостный – реактивный – ток может быть определён по формуле

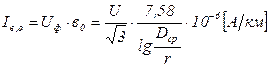, (2.11)

где U – междуфазное напряжение, В.

Величина ёмкостного тока на единицу длины при равномерно распределённой ёмкости (b_о = const) зависит от величины напряжения в каждой точке линии и поскольку напряжение меняется вдоль линии по величине и по фазе, то также по величине и фазе меняется и ёмкостной ток.

Однако в практических расчётах этим обстоятельством обычно пренебрегают и вместо действительного напряжения принимают номинальное напряжение сети. Ёмкостный ток в начале линии состоит из суммы единичных ёмкостных токов и поэтому ёмкостный ток возрастает от конца к началу линии пропорционально длине линии.

Ток же, обусловленный нагрузкой, не зависит от длины линии. Так как суммарный ток линии определяется геометрическим сложением в каждой точке линии тока нагрузки и ёмкостного тока, то он имеет величину, изменяющуюся по длине линии.

<12 3 4 5 6 7 >

Дата добавления: 2017-06-13; просмотров: 7530;