Корректирующие коды
Корректирующими называются коды позволяющие обнаруживать и исправлять ошибки. Они характеризуются кодовым (или хэмминговым) расстоянием, обозначающимся буквой d.
Кодовое расстояние – это то минимальное число элементов, в которых одна кодовая комбинация отличается от другой. Для определения кодового расстояния достаточно сравнить две кодовые комбинации по модулю 2.
Так, сложив две комбинации определим, что расстояние между ними d = 7.
11001010101
Код с n = 3 и d = 1 для передачи используются все восемь кодовых комбинаций 000, 001, .., 111. Такой код является не помехоустойчивым, он не в состоянии обнаружить ошибку.
Если выберем комбинации с кодовым расстоянием d = 2, например, 000,110,101,011, то такой код позволит обнаруживать однократные ошибки. Назовем эти комбинации разрешенными, предназначенными для передачи информации. Все остальные 001, 010, 100, 111 – запрещенные. Любая одиночная ошибка приводит к тому, что разрешенная комбинация переходит в ближайшую, запрещенную комбинацию. Получив запрещенную комбинацию, мы обнаружим ошибку.
Комбинации для кода с d = 3:
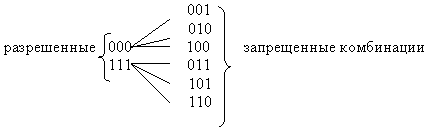
Такой код может исправить одну одиночную ошибку или обнаружить две ошибки. Таким образом, увеличивая кодовое расстояние можно увеличить помехоустойчивость кода. В общем случае кодовое расстояние определяется по формуле d = (S + r)+ 1, где S - число исправляемых ошибок , r - число обнаруживаемых ошибок. Обычно r > S.
Большинство корректирующих кодов являются линейными кодами. Линейные коды – это такие коды, у которых контрольные символы образуются путем линейной комбинации информационных символов.
Кроме того, корректирующие коды являются групповыми кодами. Групповые коды (Gn) – это такие коды, которые имеют одну основную операцию. При этом должно соблюдаться условие замкнутости (то есть, при сложении двух элементов группы получается элемент, принадлежащий этой же группе). Число разрядов в группе не должно увеличиваться. Этому условию удовлетворяет операция поразрядного сложения по модулю 2. В группе, кроме того, должен быть нулевой элемент.
Примеры кодовых комбинаций:
1) 1101 1110 0111 1011 – не группа, так как нет нулевого элемента;
2) 0000 1101 1110 0111 – не группа, так как не соблюдается условие замкнутости (1101 + 1110 = 0011);
3) 000 001 010 011 100 101 110 111 – группа;
4) 000 001 010 111 – подгруппа.
Большинство корректирующих кодов образуются путем добавления к исходной m – комбинации k – контрольных символов. В итоге в линию передаются n = m + k символов. При этом корректирующие коды называются (n,m) кодами.
Для построения кода способного обнаруживать и исправлять одиночную ошибку необходимое число контрольных разрядов будет составлять n - m ≥ log (n + 1).
Если необходимо исправить две ошибки, то число различных исходов будет составлять Cn2. Тогда n - m ≥ log (1 + Cn1 + Cn2), в этом случае обнаруживаются однократные и двукратные ошибки. В общем случае, число контрольных символов должно быть не меньше:
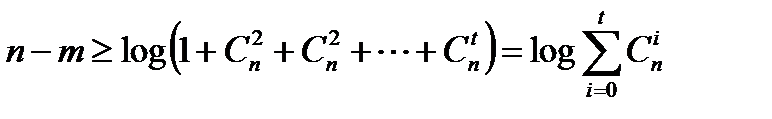 .
.
Эта формула называется неравенством Хэмминга, или нижней границей Хэмминга для числа контрольных символов.
Код Хэмминга.Код Хэмминга, являющийся групповым (n,m) кодом, с минимальным расстоянием d=3 позволяет обнаруживать и исправлять однократные ошибки. Построение кодов Хемминга базируется на принципе проверки на чётность веса W (числа единичных символов) в информационной группе кодового блока.
Для каждого числа проверочных символов k = 3,4,5… существует классический код Хемминга с маркировкой (n,m) = (2k -1, 2k -1 - k), т.е. – (7,4), (15,11), (31,26) …
Для примера рассмотрим классический код Хемминга (7,4). В простейшем варианте при заданных четырёх (m = 4) информационных символах (i1, i2, i3, i4) будем полагать, что они сгруппированы в начале кодового слова, хотя это и не обязательно. Дополним эти информационные символы тремя проверочными символами (k = 3), задавая их следующими равенствами проверки на чётность, которые определяются соответствующими алгоритмами:
k1 = i1  i2
i2  i3;
i3;
k2 = i2  i3
i3  i4;
i4;
k3 = i1  i2
i2  i4, где знак
i4, где знак  означает сложение по модулю 2.
означает сложение по модулю 2.
В соответствии с этим алгоритмом определения значений проверочных символов ki возможны 16 кодовых слов (7,4) – кода Хемминга.
| m = 4 | k = 3 | |||||
| i1 | i2 | i3 | i4 | k1 | k2 | k3 |
На вход декодера поступает кодовое слово V = (i1', i2', i3', i4', k1', k2', k3'), апостроф означает, что любой символ слова может быть искажён помехой в канале передачи.
В декодере в режиме исправления ошибок строится последовательность:
s1 = k1'  i1'
i1'  i2'
i2'  i3';
i3';
s2 = k2'  i2'
i2'  i3'
i3'  i4';
i4';
s3 = k3'  i1'
i1'  i2'
i2'  i4'.
i4'.
Трёхсимвольная последовательность (s1, s2, s3) называется синдромом S.
Синдром S = (s1, s2, s3) представляет собой сочетание результатов проверки на чётность соответствующих символов кодовой группы и характеризует определённую конфигурацию ошибок (шумовой вектор).
Число возможных синдромов определяется выражением: S = 2k.
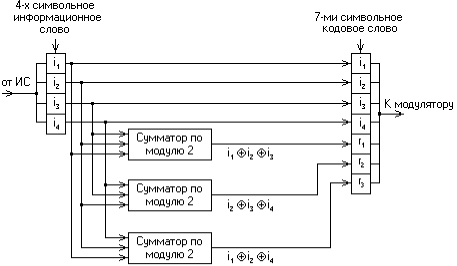
Рис. 16.1. Кодер простого (7, 4) – кода Хемминга
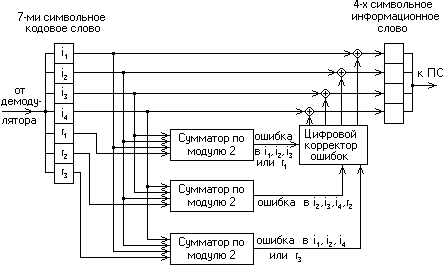
Рис. 16.2. Декодер простого (7, 4) – кода Хемминга
При числе проверочных символов k = 3 имеется восемь возможных синдромов (23 = 8). Нулевой синдром (000) указывает на то, что ошибки при приёме отсутствуют или не обнаружены. Всякому ненулевому синдрому соответствует определённая конфигурация ошибок, которая и исправляется. Классические коды Хемминга имеют число синдромов, точно равное их необходимому числу, позволяют исправить все однократные ошибки в любом информативном и проверочном символах и включают один нулевой синдром. Такие коды называются плотноупакованными.
Усечённые коды являются неплотноупакованными, так как число синдромов у них превышает необходимое. Так, в коде (9,5) при четырёх проверочных символах число синдромов будет равно 24 =16, в то время как необходимо всего 10. Лишние 6 синдромов свидетельствуют о неполной упаковке кода (9,5). Для рассматриваемого кода (7,4) в таблице 16.1 представлены ненулевые синдромы и соответствующие конфигурации ошибок.
Таким образом, код (7,4) позволяет исправить все одиночные ошибки. Простая проверка показывает, что каждая из ошибок имеет свой единственный синдром. При этом возможно создание такого цифрового корректора ошибок (дешифратора синдрома), который по соответствующему синдрому исправляет соответствующий символ в принятой кодовой группе.
Таблица 16.1
Соответствие синдромов конфигурациям ошибок
| Синдром | |||||||
| Конфигурация ошибок | |||||||
| Ошибка в символе | k3 | k2 | i4 | k1 | i1 | i3 | i2 |
Циклические коды.Циклическим кодом называется такой групповой код, который связан дополнительным условием цикличности. Все строки образующей матрицы такого кода могут быть получены циклическим сдвигом одной комбинации, называемой образующей для данного кода.
Циклические коды широко применяются при передаче данных в современных информационных системах благодаря ряду положительных качеств, основными из которых являются:
- высокая эффективность, так как циклические коды обладают сравнительно небольшой избыточностью, отличаются простотой реализации кодирующих и декодирующих устройств;
- высокая помехоустойчивость – за счет способности кода к обнаружению и исправлению ошибок.
Для оптимального кода количество исправляемых ошибок равно 2k-1, где k – число контрольных разрядов.
Применяемые в настоящее время циклические коды, содержащие n разрядов, из которых m является информационными, а k = n-m – контрольными (проверочными), расположенными в конце кодовой комбинации. Так как информационные и контрольные разряды занимают строго определенные места и длина кодовой комбинации постоянна, то циклические коды относятся к систематическим кодам.
Для описания циклических кодов обычно пользуются записью любого n-разрядного двоичного числа в виде многочлена степени (n-1). Например, кодовая комбинация 1011001 записывается как многочлен x6 + x4 + x3 + 1, т.е. коэффициенты многочлена не пишутся, а члены с коэффициентами 0 опускаются. Наивысшая степень числа с коэффициентом 1 называется степенью полинома (многочлена). Так, в примере рассмотрен многочлен 6-й степени.
Таким образом, действия над кодовыми числами можно свести к действиям над многочленами. При этом используют теорию коммутативных колец. Коммутативным кольцом называют множество, в котором особым образом определены операции сложения и умножения.
В циклическом кодировании все математические операции сложения производятся с использованием сложения по mod 2 и с приведением подобных членов.
Операцию умножения символически проводят по следующим правилам:
1) Вначале все многочлены перемножаются по обычным правилам, но с приведением подобных членов по mod 2.
2) Если старшая степень полученного в результате умножения многочлена не превышает (n-1), то этот многочлен является результатом символического умножения.
3) Если старшая степень полученного в результате умножения многочлена больше (n-1), то многочлен произведения делится на двучлен xn+1. В этом случае результатом символического умножения считается остаток от деления (вычет).
Пример: Имеем кодовые комбинации 001101 и 101110, где n = 6.
Эти комбинации соответствуют многочленам: x3 + x2 + 1 и x5 + x3 + x2 + x.
Допустим, необходимо провести дважды циклический сдвиг этих кодовых комбинаций. В результате получим:
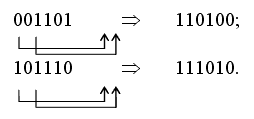
Для проведения этой операции с многочленами необходимо их символически умножить на x×x = x2:
1) (x3 + x2 + 1) × x2 = x5 + x4 + x2, т.к. степень полученного многочлена не превышает (n-1) = 5, то этот многочлен принимается за результат умножения и действительно соответствует сдвинутой кодовой комбинации 110100.
2) (x5 + x3 + x2 + x) × x2 = x7 + x5 + x4 + x3, т.к. степень полученного многочлена превышает (n-1), то для получения результата символического умножения необходимо произвести деление этого многочлена на двучлен (xn +1):
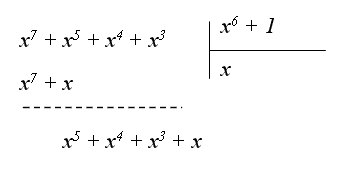
Остаток от деления x5 + x4 + x3 + x принимается за результат символического умножения, что соответствует циклически сдвинутой кодовой комбинации 111010.
В основе образования циклического кода лежит использование так называемого образующего (неприводимого) многочлена (полинома). Выбор образующего полинома определяет тип циклического кода и характеризует его обнаруживающие и исправляющие способности.
Степень образующего полинома равна k, т.е. числу контрольных символов. Любой многочлен циклического кода должен делиться без остатка на образующий полином.
В то же время ни один многочлен, соответствующий запрещенной кодовой комбинации, не должен делиться без остатка на образующий полином. Это свойство позволяет обнаружить ошибку, а по виду остатка и вектор ошибки, т.е. исправлять ошибки.
Для получения циклического кода, многочлен G(x) (соответствующий кодовым комбинациям безызбыточного m – разрядного кода), умножают на xk. Это соответствует приписыванию со стороны младших разрядов k нулей к кодовым комбинациям.
Затем произведение G(x)×xk делится на образующий многочлен Р(x). В общем случае мы получаем в результате такого деления Q(x) той же степени, что и G(x) и остаток R(x). Остаток R(x) прибавляется к G(x)×xk. Получаем многочлен F(x) = G(x)×xk + R(x).
Так как в комбинациях, соответствующих многочлену G(x)×xk, первые k младших разрядов – нули, а R(x) – многочлен степени не выше k-1, то операция получения многочлена соответствует приписыванию R(x) к G(x) со стороны младших разрядов.
Полученный таким образом многочлен F(x) будет делиться на образующий многочлен Р(x) без остатка.
Таким образом, циклический код можно получить, если к каждой кодовой комбинации безызбыточного кода приписывать остаток от деления многочлена, соответствующего этой кодовой комбинации на образующий многочлен.
Так как опознавателями ошибок являются остатки от деления многочленов циклического кода на образующий многочлен, то корректирующая способность кода будет тем выше, чем больше остатков от деления можно образовать. Наибольшее число остатков, равное 2k-1 (исключая нулевой), может обеспечить неприводимый (простой) многочлен, т.е. такой многочлен, который делится только сам на себя. Поэтому в качестве образующего многочлена необходимо выбирать простой многочлен (или их произведение).
Пример образования циклического кода.Пусть информационный код содержит m = 4 разрядов. Одна из N = 2m комбинаций этого кода: 1101 в виде многочлена запишется так: G(x) = x3 + x2 + 1.
Если циклический код обнаруживает и исправляет одну ошибку, его минимальное кодовое расстояние равно: dmin = S + r + 1 = 3 (где r - число обнаруживаемых, а S - число исправляемых ошибок).
Выберем из Таблицы 16.2 значение k (для m = 4, k = 3).
Выберем из таблицы 16.3 полином P(x) для k = 3: P(x) = x3 + x + 1 (т.е. 1011)
Умножим G(x) на xk: G(x)×x3 = (x3 + x2 + 1)×x3 = x6 + x5 + x3 (т.е. 1101 × 1000 = 1101000)
Разделим G(x)×xk на полином P(x):
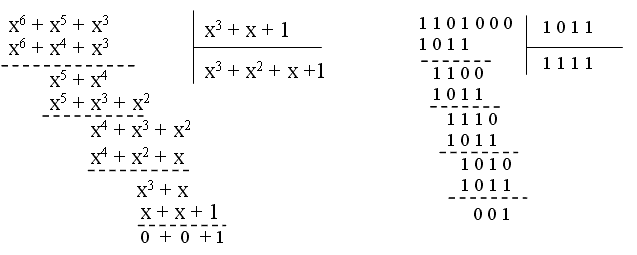
В результате получаем:
G(x)×x3/ P(x) = (x3 + x2 + x + 1) + 001/ (x3 + x + 1) или: 1111+001/1011
В соответствии с n = m + k: (x3 + x2 + x + 1) = Q(x) → 1111
1/(x3 + x + 1) = R(x) / P(x) → 001 / 1011
R(x) = 001
Искомый многочлен F(x) равен:
F(x) = Q(x) × P(x) = G(x) × xk + R(x) = x6 + x5 + x3 + 1 → 1101001
Для обнаружения и исправления ошибок принятая комбинация делится на образующий многочлен P(х). Если остаток R(х) = 0, значит, комбинация принята без ошибок. Наличие остатка свидетельствует о том, что комбинация принята искаженной.
Таблица 16.2
Зависимость между n, m и k
| n | 9...15 | 17…31 | 33…63 | 65…127 | ||||
| m | 5…11 | 12…26 | 27…57 | 28…120 | ||||
| k |
Таблица 16.3
Неприводимые полиномы P(x)
| Неприводимые многочлены | Их эквиваленты |
| q(x) = x + 1 | |
| q(x2) = x2 + x + 1 | |
| q(x3) = x3 + x + 1 | |
| q(x3) = x3 + x2 + 1 | |
| q(x4) = x4 + x + 1 | |
| q(x4) = x4 + x3 + 1 | |
| q(x4) = x4 + x3 + x2 + x + 1 | |
| q(x5) = x5 + x2 + 1 | |
| q(x5) = x5 + x3 + 1 | |
| q(x5) = x5 + x3 + x2 + x + 1 | |
| q(x5) = x5 + x4 + x2 + x + 1 | |
| q(x5) = x5 + x4 + x3 + x + 1 | |
| q(x5) = x5 + x4 + x3 + x2 + 1 | |
| q(x6) = x6 + x + 1 | |
| q(x7) = x8 | |
| q(x8) = x8 + x4 + x3 + x2 + 1 | |
| q(x9) = x9 + x4 + 1 | |
| q(x10) = x10 + x3 + 1 |
Если число проверочных символов меньше числа информационных символов, то проще комбинации циклического кода получить и с помощью образующей матрицы.
Образующая матрица состоит из двух подматриц – основной и дополнительной.
Основная матрица – это единичная транспортированная матрица Im. Она содержит m столбцов и m строк (по числу информационных разрядов кода).
Дополнительная матрица – матрица остатков. Она образуется путем деления на образующий полином P(x) многочлена в виде единицы с рядом нулей и выписыванием всех промежуточных остатков. Эта матрица содержит k столбцов и m строк.
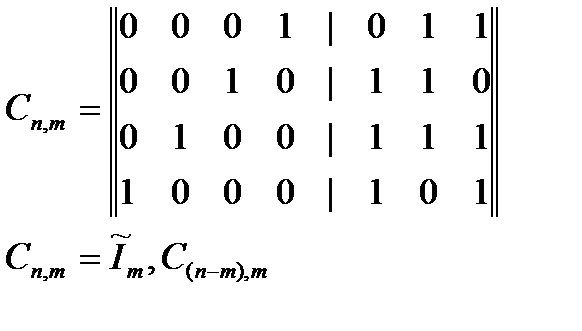
С помощью образующей матрицы можно получить любую из N = 2m-1 разрешенных комбинаций циклического кода. Каждая из строк образующей матрицы – это уже комбинация циклического кода. Остальные N-m комбинаций можно получить сложением по модулю 2 строк матрицы.
Пример:
Кодеры и декодеры циклических кодов в основном выполняют операции умножения и деления многочленов.
Операция деления на образующий полином P(x) осуществляется также с помощью регистра сдвига, но в этом случае регистр имеет обратные связи, включенные через сумматоры по модулю 2. Деление многочленов – это операция сложения по модулю 2 делителя с разрядами делимого, начиная со старшего разряда.
Для алгоритма кодирования используется k-разрядный регистр сдвига с обратными связями через сумматоры по модулю 2. Число сумматоров равно числу членов образующего полинома, отличных от нуля, минус единица. Структурная схема кодирующего устройства приведена ниже на рисунке 16.3.
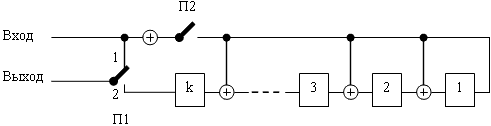
Рис. 16.3. Структурная схема кодирующего устройства
Схема работает следующим образом. В начальном состоянии ключ П2 замкнут, ключ П1 находится в положении «1». Информационная кодовая комбинация а(x), имеющая m разрядов (символов) подается на вход через «1» П1 и одновременно в регистр сдвига Р1. За k тактов работы регистра Р1 в нем формируется остаток r(x), который представляет собой контрольные разряды (символы) циклического кода. После этого ключ П2 размыкается, ключ П1 переводится в положение «2» и контрольные символы за k тактов работы регистра Р1 выводятся из него, следуя за информационными символами.
Необходимо иметь в виду, что информационная комбинация а(x) поступает на вход кодера в обратной последовательности, т.е. начиная со старших разрядов. Комбинация циклического кода на выходе кодера имеет такую же последовательность.
Схема декодирования (образуется с помощью деления на образующий многочлен):
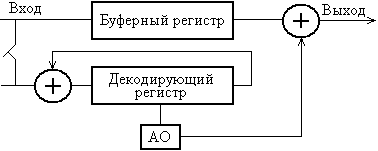
Рис. 16.4. Схема декодирования циклического кода. АО - анализатор ошибок.
Исходная комбинация подается в буферный регистр и одновременно через ключ в декодирующий регистр. Если с приходом последнего символа, зафиксирован нулевой остаток, то ошибок нет, и, если не нулевой, то есть ошибка. Принятая комбинация подается через выходной сумматор, и искаженный сигнал исправляется анализатором ошибок (АО).
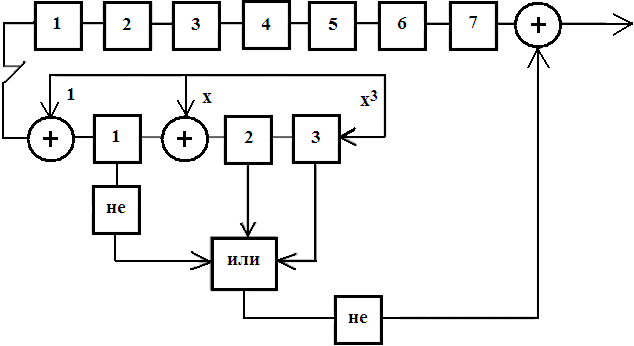
Рис. 16.5. Пример схемы декодирования методом деления на полином P(x) = x3+x+1
Коды Рида-Соломона.Коды Рида-Соломона являются субнабором циклических кодов и представляют собой линейные блочные коды. Код Рида-Соломона специфицируются как RS(n,m) s-битных символов.
Это означает, что кодировщик воспринимает m информационных символов по s бит каждый и добавляет символы четности для формирования n символьного кодового слова. Имеется n-m символов четности по s бит каждый. Декодер Рида-Соломона может корректировать до k / 2 символов, которые содержат ошибки в кодовом слове, где k = n - m.
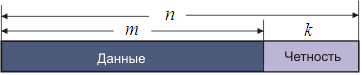
Рис. 16.6. Структура кодового слова R-S
Пример. Популярным кодом Рида-Соломона является RS(255,223) с 8-битными символами. Каждое кодовое слово содержит 255 байт, из которых 223 являются информационными и 32 байтами четности. Для этого кода: n = 255, m = 223, s = 8, k = 32, k / 2 = 16.
Декодер может исправить любые 16 символов с ошибками в кодовом слове: то есть, ошибки могут быть исправлены, если число искаженных байт не превышает 16.
Коды Рида-Соломона базируются на специальном разделе математики – полях Галуа (GF), или конечных полях. Арифметические действия (+, -, x, / и др.) над элементами конечного поля дают результат, который также является элементом этого поля. Для реализации этих арифметических операций требуется специальное оборудование и/или специализированное программное обеспечение.
Общая форма образующего полинома имеет вид:
P(x) = (x-ai)(x-ai+1)…(x-ai+k),
кодовое слово формируется с помощью операции:
F(x) = P(x).i(x),
где P(x) – образующий полином, i(x) представляет собой информационныйблок, F(x) – кодовое слово, называемое простым элементом поля.
ПОМЕХОУСТОЙЧИВОСТЬ
Дата добавления: 2017-10-04; просмотров: 7075;











