Спектральное представление периодических сигналов

Как известно, разложение периодического сигнала по базису тригонометрических функций – это разложение его в ряд Фурье.

Разложение сигнала в ряд Фурье называется спектром сигнала.

В общем случае периодический сигнал содержит независящую от времени постоянную составляющую и бесконечный набор гармонических колебаний, или гармоник, с частотами, кратными основной частоте последовательности.

Графическое изображение коэффициентов ряда Фурье для конкретного сигнала называется спектральной диаграммой. По горизонтальной оси откладываются частоты гармоник, а по вертикали – амплитуды (амплитудная диаграмма) или начальные фазы (фазовая диаграмма).

При разложении в комплексный ряд Фурье:

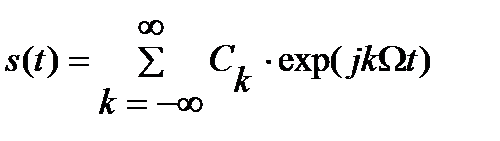, (3.1)

где .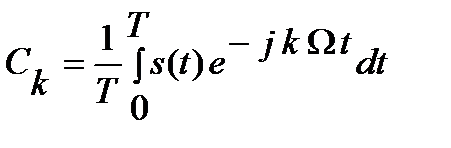

Спектр сигнала содержит компоненты на отрицательной полуоси частот, причём С_-k = С_k* (* обозначено комплексно-сопряжённое число).

Между коэффициентами комплексного и тригонометрического ряда существует связь:

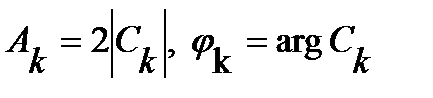. (3.2)

Шириной спектра сигнала ΔF_эназывается полоса частот, в пределах которой заключена основная доля энергии сигнала.

В качестве примера рассчитаем спектр периодической последовательности прямоугольных импульсов c амплитудой А:

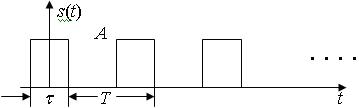
Рис. 3.1. Периодическая последовательность прямоугольных импульсов

Определим коэффициенты разложения в ряд Фурье C_к:

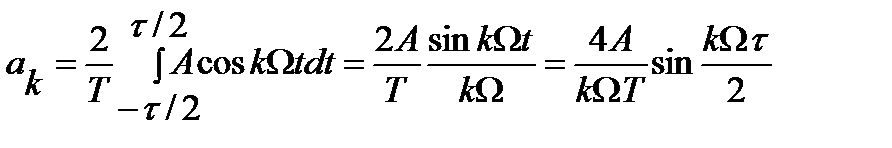
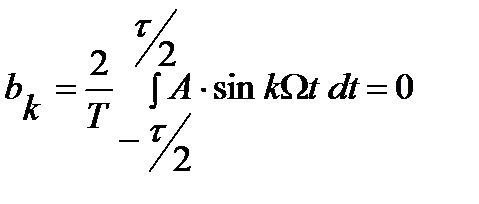, т.к. подынтегральная функция – нечетная.

Пусть Т = 2t, тогда коэффициенты a_k равны:

a₀ = А, a_k = 2А/ kp (sin kp/2), при k > 0.

Итак, временная диаграмма периодической последовательности импульсов показана на рис. 3.1. Спектр этой последовательности дискретный и показан на рис. 3.2.

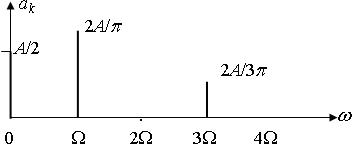
Рис. 3.2. Спектр периодическая последовательность прямоугольных импульсов

Ширина спектра сигнала равна, в данном случае, ΔF_э =2p/t.