Математическое представление сигналов

Многие задачи теории связи и радиотехники, например вычисление отклика физической системы на известное входное воздействие, требуют специфической формы представления сигналов.

Способ получения таких моделей сигналов состоит в следующем. Реальный сигнал приближенно представляется суммой некоторых элементарных сигналов, возникающих в последовательные моменты времени. Если теперь устремить к нулю длительность отдельных элементарных сигналов, то, естественно, в пределе будет получено точное представление исходного сигнала. В литературе этот способ описания сигнала получил название динамического представления, подчеркивающее развивающийся во времени процесс.

Широкое применение нашли два способа динамического представления. Согласно первому из них в качестве элементарных сигналов используются ступенчатые функции, возникающие через равные промежутки времени ∆.

В качестве таких функций используются функции включения (рис. 2.3.) или функции Хевисайда σ(t), которые описываются следующим образом

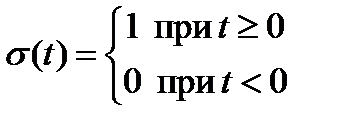
Рис. 2.3. Функция включения

Другая возможность представления сигнала заключается в использовании стандартных прямоугольных функций длительностью ∆. На рис. 2.4 показаны возможные способы представления сигналов.

Рис. 2.4. Динамическое представление сигналов

Как видно (рис. 2.4а), текущее значение сигнала при любом t равно сумме ступенчатых функций

s(t) ≈ s₀ σ(t) + (s₁ - s₀ )σ(t - Δ) + (s₂ - s₁ ) σ(t - 2Δ) + ··· (2.2)

В случае представления аналогового сигнала суммой примыкающих к друг другу прямоугольных импульсов, элементарный импульс с номером k представляется в виде

u_k(t) = s_k[σ(t - t_k ) - σ(t - t_k - Δ)]. (2.3)

Тогда исходный сигнал является суммой элементарных импульсов

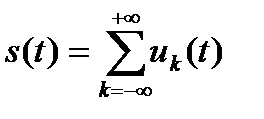. (2.4)

Важное значение при динамическом представлении сигнала играет и другая функция, которая называется дельта-функцией δ(t) или функцией Дирака. Такой функцией называется импульсный сигнал, площадь которого, например, A_m ·τ равна 1, причем длительность импульса τ стремится к нулю, а амплитуда импульса A_m стремится к бесконечности.

Если в выражении (2.4) Δ устремить к нулю, то получим формулу динамического представления сигнала

(2.5)

Таким образом, если непрерывную функцию умножить на дельта функцию и произведение проинтегрировать по времени, то результат будет равен значению функции в той точке, где существует δ-функция. В этом заключается фильтрующее свойство дельта-функции.