Сигналы с ограниченным спектром. Теорема Котельникова

Разложение непрерывных сигналов в ряд Котельникова

Как отмечено ранее, любые сигналы конечной длительности теоретически имеют бесконечно широкий спектр частот. В то же время доля энергии, передаваемая на высоких частотах, очень мала и ею при расчете полной энергии сигнала можно пренебречь. Следовательно, сигналы с ограниченным спектром являются удобными математическими моделями реальных сигналов.

В 1933 году В. А. Котельников доказал, что сигнал s(t) с ограниченной полосой частот, не имеющий спектральных компонент с частотами, которые превышают значение ω_в = 2πF_в, однозначно определяется значениями, выбранными через равные промежутки времени [1]

Δt = π/ω_в = 1/2F_в.

Известно, что при аналогово-цифровом преобразовании, чем меньше частота оцифровки (или больше период дискретизации) и грубее квантование сигнала, тем меньше данных необходимо для представления аналогового сигнала в цифровом виде. С другой стороны с уменьшением объема данных увеличивается вероятность потери информации содержащейся в сигнале.

Чтобы продемонстрировать искажение информации при неправильном выборе частоты дискретизации сигнала рассмотрим примеры.

Пример.

Гармонический сигнал имеет частоту f (период T = 1/f). Проведем дискретизацию сигнала с периодом дискретизации T_д меньшим половины периода входного сигнала T (рис. 4.1).

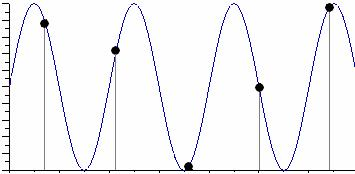
Рис. 4.1. Дискретизация сигнала с периодом Т_д < Т/2

Очевидно, что дискретные отсчеты сигнала однозначно не отображают форму исходного сигнала, в частности по получившимся точкам можно построить гармонический сигнал с периодом T_искаж., отличающимся от периода исходного сигнала T. Период T_искаж. больше периода исходного сигнала T, соответственно частота меньше, частоты исходного сигнала f (рис. 4.2).

Данный эффект называется стробоскопическим эффектом или алиасингом. Он заключается в появлении ложной низкочастотной составляющей при дискретизации сигнала с частотой меньшей удвоенной частоты исходного сигнала (или с периодом большим половины периода исходного сигнала), отсутствующей в исходном сигнале.

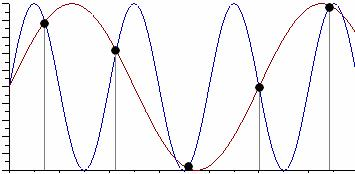
Рис. 4.2. Стробоскопический эффект дискретизации

При дискретизации с периодом равным половине исходного аналогового сигнала (f_д = 2f) возникает неопределенность начальной фазы и амплитуды сигнала, т.е. возможно зеркальное искажение (противофаза), при этом частота исходного сигнала не искажается. В крайнем случае, мы можем получить отсчеты сигнала равные нулю (рис. 4.3).

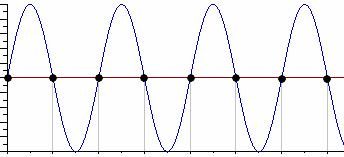
Рис. 4.3. Дискретизация сигнала с периодом Т_д = Т/2

Если период дискретизации меньше половины периода исходного сигнала, то очевидно, что через получившиеся после оцифровки точки можно построить только один гармонический сигнал, соответствующий исходному, без искажения начальной фазы, амплитуды и частоты (рис. 4.4).

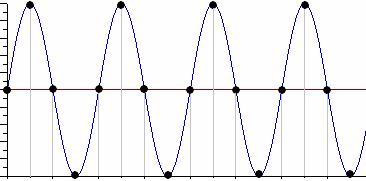
Рис. 4.4. Дискретизация сигнала с периодом Тд < Т/2

Таким образом, для адекватного восстановления гармонического сигнала по дискретным отсчетам, период дискретизации должен быть не меньше половины периода сигнала. Частота равная половине частоты дискретизации называется частотой Найквиста f_N = f_д/2.

Таким образом, аналоговый сигнал с ограниченным спектром может быть восстановлен однозначно и без искажений по своим дискретным отсчетам, взятым с частотой большей удвоенной максимальной частоты его спектра F_д > 2·F_max.

Данное утверждение известно как теорема Котельникова (в западной литературе теорема Найквиста-Шеннона) или теорема отсчетов.

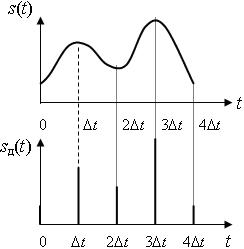
Рис. 4.5. Временные диаграммы непрерывного сигнала s(t) и дискретизированного s_д(t)

Важно, что не надо передавать непрерывно исходный сигнал s(t), достаточно передавать отсчёты s(kDt). Это первый шаг перехода от непрерывного сигнала к цифровому. С точки зрения математики теорема Котельникова означает представление сигнала в виде ряда:

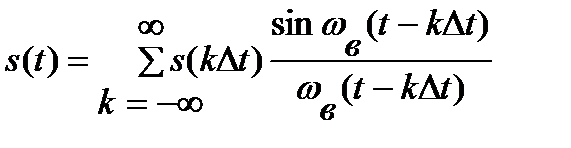, (4.1)

где s(k∆t) – отсчёты;

(sin ω_в(t - k∆t)) / ω_в(t - k∆t) – функции отсчётов.

Ряд Котельникова – это разложение сигнала s(t) в ряд по ортогональным функциям φ_k(t).

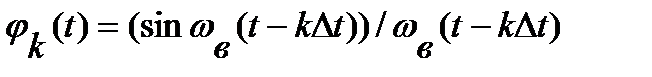(4.2)

Теоретически дискретизация осуществляется с помощью d-импульсов.

;

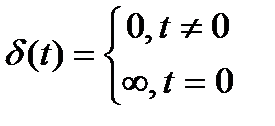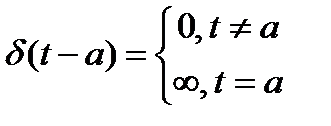
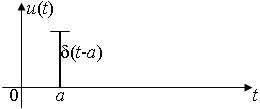
Рис. 4.6. Временная диаграмма одиночного d-импульса

Спектр одиночного d-импульса получим, используя преобразование Фурье:

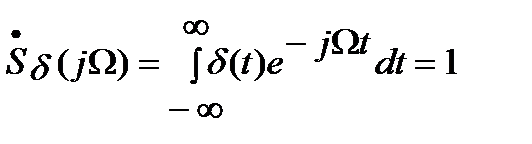
Использовано "фильтрующее" свойство дельта-функций:

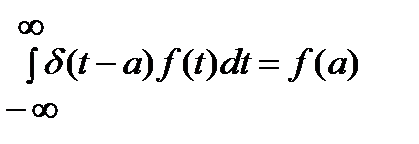
Следовательно, спектр одиночного дельта-импульса имеет вид:

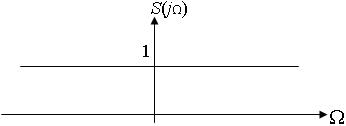
Рис. 4.7. Спектр одиночного δ-импульса

Чтобы получить отсчёты функции s(t) перемножим функцию s(t) на периодическую последовательность дельта-импульсов с периодом Т = Dt.

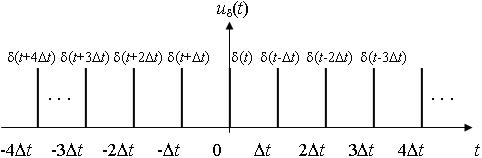
Рис. 4.8. Временная диаграмма периодической последовательности

δ-импульсов

Так как сигнал периодический, то его спектр будет дискретным.

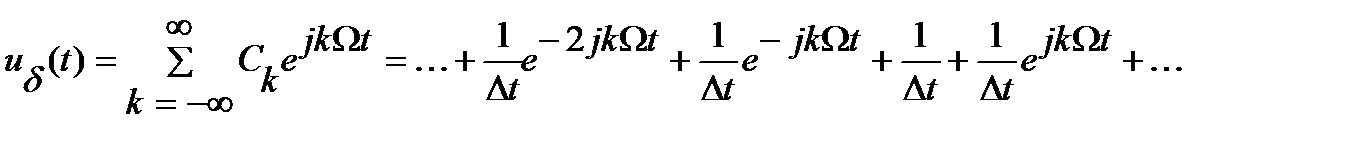(4.3)

;

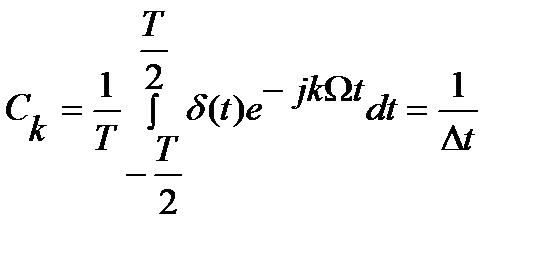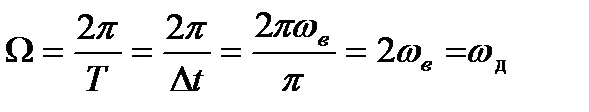
Т = Dt; ω_д – частота дискретизации.

Спектр периодической последовательности дельта-импульсов в соответствии с формулой для U(t) имеет следующий вид:

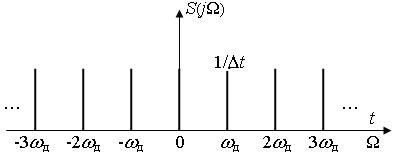
Рис. 4.9. Спектр периодической последовательности δ-импульсов