Плоская система произвольно расположенных сил

<1 234 5 6 7 >

Главный вектор равен геометрической суммевекторов произвольной плоской системы сил. Проецируем все силы системы на оси координат и, сложив соответствующие проекции на оси, получим проекции главного вектора.

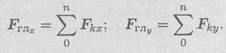
По величине проекций главного вектора на оси координат находим модуль главного вектора:

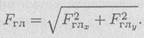
Главный момент системы сил равен алгебраической сумме моментов сил системы относительно точки приведения.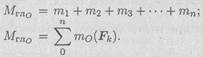

Таким образом, ПСПРС приводится к одной силе (главному вектору системы сил) и одному моменту (главному моменту системы сил).

Три формы условия равновесия ПСПРС

Для разных случаев используются три группы уравнений равновесия.

Для частного случая, если уравновешена система параллельных сил, можно составить только два уравнения равновесия:

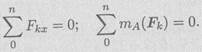
Балочные системы. Определение реакций опор и моментов защемления

Виды нагрузок

По способу приложения нагрузки делятся на сосредоточенные и распределенные. Если реально передача нагрузки происходит на пренебрежимо малой площадке (в точке), нагрузку называют сосредоточенной.

Часто нагрузка распределена по значительной площадке или линии (давление воды на плотину, давление снега на крышу и т.п.), тогда нагрузку считают распределенной.

В задачах статики для абсолютно твердых тел распределенную нагрузку можно заменить равнодействующей сосредоточенной силой (рис. 6.1).

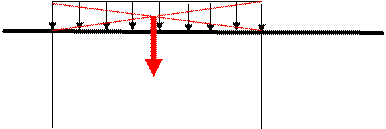l/2Q

l

q — интенсивность нагрузки, Н/м;

l— линия действия распределенной нагрузки, м;

Q = ql — равнодействующая распределенной нагрузки.

Разновидности опор балочных систем (см. реакции и их связи)Балка — конструктивная деталь в виде прямого бруса, закрепленная на опорах и изгибаемая приложенными к ней силами.

Высота сечения балки незначительна по сравнению с длиной. Жесткая заделка (защемление) (рис. 6.2)

Опора не допускает перемещений и поворотов. Заделку заменяют двумя составляющими силами RaxиR_Ayи парой с моментом Mr_А.

Для определения этих неизвестных удобно использовать систему уравнений в виде

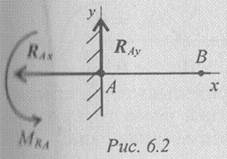
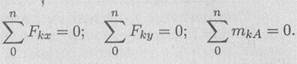
Каждое уравнение имеет одну неизвестную величину и решается без подстановок. Для контроля правильности решений используют дополнительное равнение моментов относительно любой точки на балке, например В:

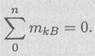
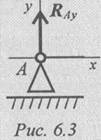
Шарнирно-подвижная опора (рис. 6.3).

Опора допускает поворот вокруг шарнира и перемещениевдоль опорной поверхности. Реакция направлена перпендикулярно опорной поверхности.

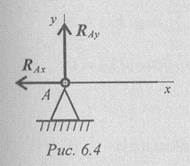
Шарнирно-неподвижная опора (рис. 6.4)

Опора допускает поворот вокруг шарнира и может быть заменена двумя составляющими силы вдоль осей координат.

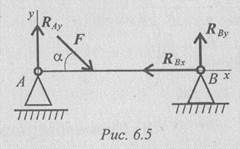
Балка на двух шарнирных опорах (рис. 6.5)

Тема 1.4. Центр тяжести

Сила тяжести — это сила, с которой тело притягивается к Земле, она распределена по всему объему тела.

Цент тяжести –это точка приложения силы тяжести.

Формулы для определения центра тяжести плоских фигур:

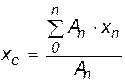
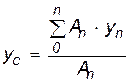
где А_n — площадь простейшей (элементарной) фигуры;

x_n, y_n — координаты центра тяжести простейшей (элементарной) фигуры.

Выражение 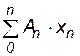называют статическим моментом площади (S_y).

Координаты центра тяжести сечения можно выразить через статический момент: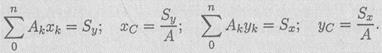

Оси, проходящие через центр тяжести, называются центральными осями. Статический момент относительно центральной оси равен нулю.

<1 234 5 6 7 >

Дата добавления: 2017-10-04; просмотров: 3509;