Тема 2.1. Основные положения.
«Сопротивление материалов» — это раздел «Технической механики», в котором излагаются теоретико-экспериментальные основы и методы расчета наиболее распространенных элементов конструкций на прочность, жесткость и устойчивость.
В сопротивлении материалов пользуются данными смежных дисциплин: физики, теоретической механики, материаловедения, математики и др. В свою очередь сопротивление материалов как наука является опорной базой для целого ряда технических дисциплин.
Любые создаваемые конструкции должны быть не только прочными и надежными, но и недорогими, простыми в изготовлении и обслуживании, с минимальным расходом материалов, труда и энергии.
Расчеты сопротивления материалов являются базовыми для обеспечения основных требований к деталям и конструкциям.
Виды расчетов
Расчет на прочность обеспечивает не разрушение конструкции.
Расчет на жесткость обеспечивает деформации конструкции нагрузкой в пределах допустимых норм.
Расчет на выносливость обеспечивает необходимую долговечность элементов конструкции.
Расчет на устойчивость обеспечивает сохранение необходимой формы равновесия и предотвращает внезапное искривление длинных стержней.
Для обеспечения прочности конструкций, работающих при ударных нагрузках (при ковке, штамповке и подобных случаях), проводятся расчеты на удар.
Основные гипотезы и допущения
Приступая к расчетам конструкции, следует решить, что в данном случае существенно, а что можно отбросить, т. к. решение технической задачи с полным учетом всех свойств реального объекта невозможно.
Допущения о свойствах материалов
Материалы однородные — в любой точке материалы имеют одинаковые физико-механические свойства.
Материалы представляют сплошную среду — кристаллическое роение и микроскопические дефекты не учитываются.
Материалы изотропны — механические свойства не зависят от направления нагружения.
Материалы обладают идеальной упругостью — полностью восстанавливают форму и размеры после снятия нагрузки.
В реальных материалах эти допущения выполняются лишь отчасти, но принятие таких допущений упрощает расчет. Все упрощения принято компенсировать, введя запас прочности.
Классификация нагрузок и элементов конструкции
Статистические нагрузки не меняются со временем или меняются очень медленно. При действии статистических нагрузок проводится расчет на прочность.
Повторно-переменные нагрузки многократно меняют значение или значение и знак. Действие таких нагрузок вызывает усталость металла.
Динамические нагрузки меняют свое значение в короткий промежуток времени, они вызывают большие ускорения и силы инерции и могут привести к внезапному разрушению конструкции.
Из теоретической механики известно, что по способу приложения нагрузки могут быть сосредоточенными или распределенными по поверхности.
Реально передача нагрузки между деталями происходит не в точке, а на некоторой площадке, т. е. нагрузка является распределённой.
Однако если площадка контакта пренебрежительно мала сравнению с размерами детали, силу считают сосредоточенной.
При расчетах реальных деформируемых тел в сопротивлении материалов заменять распределенную нагрузку сосредоточенной не следует.
Аксиомы теоретической механики в сопротивлении материалов используются ограниченно.
Нельзя переносить пару сил в другую точку детали, перемещать сосредоточенную силу вдоль линии действия, нельзя систему сил заменять равнодействующей при определении перемещений. Всё вышеперечисленное меняет распределение внутренних сил в конструкции.
Формы элементов конструкции
Все многообразие форм сводится к трем видам по одному признаку.
1. Брус — любое тело, у которого длина значительно больше других размеров.
В зависимости от форм продольной оси и поперечных сечений различают несколько видов брусьев:
— прямой брус постоянного поперечного сечения (рис. 18.3а);
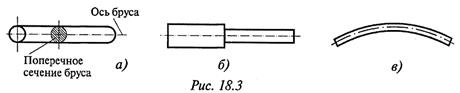
— прямой ступенчатый брус (рис. 18.3б).
— криволинейный брус (рис. 18.3в).
2. Пластина — любое тело, у которого толщина значительно меньше других размеров (рис. 18.4).

Рис. 18.4
3. Массив — тело, у которого три размера одного порядка.
Метод сечений
Метод сечений заключается в мысленном рассечении тела плоскостью и рассмотрении равновесия любой из отсеченных частей.
Если все тело находится в равновесии, то и каждая его часть находится в равновесии под действием внешних и внутренних сил.
Внутренние силы определяются из уравнений равновесия, составленных для рассматриваемой части тела.
Рассекаем тело поперек плоскостью (рис. 19.1). Рассматриваем правую часть. На нее действуют внешние силы 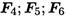 и внутренние силы упругости
и внутренние силы упругости 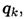 распределенные по сечению. Систему распределенных сил можно заменить главным вектором
распределенные по сечению. Систему распределенных сил можно заменить главным вектором 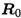 помещенным в центр тяжести сечения, и суммарным моментом сил
помещенным в центр тяжести сечения, и суммарным моментом сил 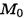 :
:
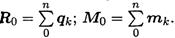
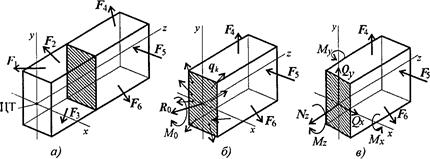
Рис. 19.1
Разложив главный вектор 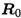 по осям, получим три составляющие:
по осям, получим три составляющие:
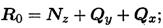
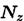 — продольная сила;
— продольная сила;
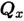 — поперечная сила по оси х;
— поперечная сила по оси х;
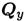 — поперечная сила по оси y.
— поперечная сила по оси y.
Главный момент тоже принято представлять в виде моментов пар сил в трех плоскостях проекции:
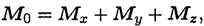
Мх — момент сил относительно Ох;
Му — момент сил относительно Оу;
Мz — момент сил относительно Оz.
Полученные составляющие сил упругости носят название внутренних силовых факторов (ВСФ). Каждый из внутренних силовых факторов вызывает определенную деформацию детали. Внутренние сивые факторы уравновешивают приложенные к этому элементу детали внешние силы.
Различают шесть внутренних силовых факторов:
Nz — продольная сила;
Qх, Qу — поперечная сила;
Мz — крутящийся момент;
Мx, Мy — изгибающий момент.
Метод сечений имеет второе название – «Правило «РОЗУ»»:
«Р» - рассекаем
«О» - отбрасываем
«З» - заменяем
«У» - уравновешиваем
Напряжения
Метод сечений позволяет определить величину внутреннего силового фактора в сечении, но не дает возможности установить закон распределения внутренних сил по сечению. Для оценки прочности необходимо определить величину силы, приходящуюся на любую точку поперечного сечения.
Величину интенсивности внутренних сил в точке поперечного сечения называют напряжением.
Напряжение характеризует величину внутренней силы, приходящейся на единицу площади поперечного сечения.
Единицы измерения Па, МПа (1МПа= 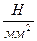 , 1Па=
, 1Па= 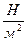 )
)
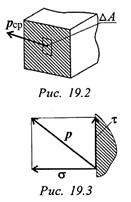
Направление напряжения рср совпадает с направлением внутренней силы в этом сечении.
Вектор рср называют полным напряжением.
Его принято раскладывать на два вектора (рис. 19.3): касательное напряжение 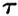 — лежащий в площадке сечения и нормальное напряжение
— лежащий в площадке сечения и нормальное напряжение 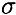 — направленный перпендикулярно площадке.
— направленный перпендикулярно площадке.
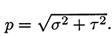
Если вектор р — пространственный, то его раскладывают на три составляющие:
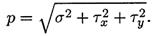
Нормальное напряжение характеризует сопротивление сечения растяжению или сжатию.
Касательное напряжение характеризует сопротивление сечения сдвигу.
Сила N (продольная) вызывает появление нормального напряжения 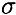 . Силы Qx и Qy вызывают появление касательных напряжений
. Силы Qx и Qy вызывают появление касательных напряжений 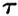 . Моменты изгибающие Мх и Му вызывают появление нормальных напряжений
. Моменты изгибающие Мх и Му вызывают появление нормальных напряжений 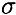 переменных по сечению.
переменных по сечению.
Крутящий момент Мz вызывает сдвиг сечения вокруг продольной оси, поэтому появляются касательные напряжения 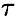 .
.
Дата добавления: 2017-10-04; просмотров: 2400;











