Метод кинетостатики

Материальная точка, движение которой в пространстве не огра­ничено какими-нибудь связями, называется свободной. Задачи реша­ются с помощью основного закона динамики.

Материальные точки, движение которых ограничено связями, называются несвободными.

Для несвободных точек необходимо определять реакции связей. Эти точки движутся под действием активных сил и ограничиваю­щих движение реакций связей (пассивных сил).

Несвободные материальные точки освобождаются от связей: связи заменяются их реакциями. Далее несвободные точки можно рассматривать как свободные (принцип освобождаемости от связей).

Сила инерции

Инертность — способность сохранять свое состояние неизмен­ным, это внутреннее свойство всех материальных тел.

Сила инерции — сила, возникающая при разгоне или торможе­нии тела (материальной точки) и направленная в обратную сторо­ну от ускорения.

Силу инерции можно измерить, она приложена к «связям» — телам, связанным с разгоняющимся или тормозящимся телом.

Рассчитано, что сила инерции равна

F_ИH = /та.

Таким образом, силы, действующие на материальные точки m₁ и m₂, при разгоне платформы соответственно равны

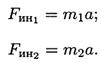
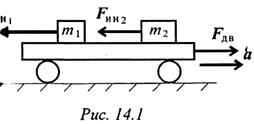
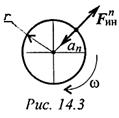
Разгоняющееся тело (плат­форма с массой т) силу инерции не воспринимает, иначе разгон платформы вооб­ще был бы невозможен. При вращательном движении (криволинейном) возникающее ускорение принято представлять в виде двух составляющих: нормального а_n и касательного a_t.

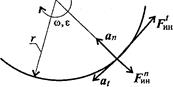
Поэтому при рассмотрении криволинейного движения могут возникнуть две составляющие силы инерции: нормальная и касательная.

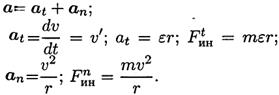
При равномерном движении по дуге всегда возникает нормаль­ное ускорение, касательное ускорение равно нулю, поэтому действует только нормальная составляющая силы инерции, направленная по радиусу из центра дуги.

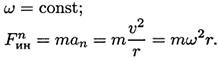
Принцип кинетостатики (принцип Даламбера)

Принцип кинетостатики используют для упрощения решения ряда технических задач.

Реально силы инерции приложены к телам, связанным с разгоняющимся телом (к связям).

Даламбер предложил условно прикладывать силу инерции к ак­тивно разгоняющемуся телу. Тогда система сил, приложенных к ма­териальной точке, становится уравновешенной, и можно при реше­нии задач динамики использовать уравнения статики.

Принцип Даламбера:

Материальная точка под действием активных сил, реакций связей и условно приложенной силы инерции находится в равнове­сии:

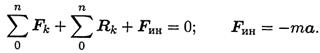
Порядок решения задач с использованием принципа Даламбера

1. Составить расчетную схему.

2. Выбрать систему координат.

3. Выяснить направление и величину ускорения.

4. Условно приложить силу инерции.

5. Составить систему уравнений равновесия.

6. Определить неизвестные величины.