Определение координат центра тяжести простейших (элементарных) плоских фигур
Примечание. Центр тяжести симметричной фигуры находится на оси симметрии. Центр тяжести стержня находится на середине высоты.
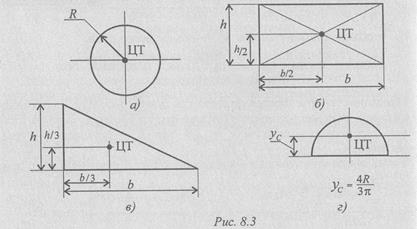
Положения центров тяжести простых геометрических фигур могут быт рассчитаны по формулам для определения центра тяжести плоских фигур(рис. 8.3):
а) — круг;
б) — квадрат, прямоугольник;
в) — треугольник;
г) — полукруг.
При решении задач используются следующие методы:
1) метод симметрии: центр тяжести симметричных фигур находится на оси симметрии;
2) метод разделения: сложные сечения разделяем на несколько простых частей, положение центров тяжести которых легко определить.
3) метод отрицательных площадей: полости (отверстия) рассматриваются как часть сечения с отрицательной площадью.
Тема 1.7. Кинематика. Основные понятия. Кинематика точки
Кинематика как наука о механическом движении, изучаемом с точки зрения геометрии. Основные понятия кинематики: механическое движение, траектория, путь, перемещение, время, скорость, ускорение.
Способы задания движения точки. Скорость. Ускорение – полное, нормальное и касательное. Виды движения точки в зависимости от ускорения
Тема 1.12. Динамика. Основные понятия и аксиомы динамики. Метод кинетостатики для материальной точки.
Динамика — раздел теоретической механики, в котором устанавливается связь между движением тел и действующими на них силами.
В динамике решают два типа задач:
— определяют параметры движения по заданным силам;
— определяют силы, действующие на тело, по заданным кинетическим параметрам движения.
При поступательном движении все точки тела движутся одинаково, поэтому тело можно принять за материальную точку. Если размеры тела малы по сравнению с траекторией, его тоже можно рассматривать как материальную точку, при этом точка падает с центром тяжести тела.
При вращательном движении тела точки могут двигаться неодинаково, в этом случае некоторые положения динамики можно применять только к отдельным точкам, а материальный объект рассматривать как совокупность материальных точек.
Поэтому динамику делят на динамику точки и динамику материальной системы.
Аксиомы динамики
Законы динамики обобщают результаты многочисленных опытов и наблюдений. Законы динамики, которые принято рассматривать как аксиомы, были сформулированы Ньютоном, но первый и четвертый законы были известны Галилею. Механику, основанную этих законах, называют классической механикой.
Первая аксиома (принцип инерции)
Всякая изолированная материальная точка находится в состоянии покоя или равномерного и прямолинейного движения, пока приложенные силы не выведут ее из этого состояния.
Это состояние называют состоянием инерции. Вывести точку из этого состояния, т.е. сообщить ей некоторое ускорение, может внешняя сила.
Всякое тело (точка) обладает инертностью. Мерой инертности является масса тела.
Массой называют количество вещества в объеме тела, в классической механике ее считают величиной постоянной. Единица измерения массы — килограмм (кг).
Вторая аксиома (второй закон Ньютона — основной закон динамики)
Ускорение, сообщенное материальной точке силой, пропорционально величине силы и совпадает с направлением силы.
F = т а,
где т — масса точки, кг;
а — ускорение точки, м/с2.
Основной закон динамики в дифференциальной форме:

На все тела на Земле действует сила тяжести, она сообщает телу ускорение свободного падения, направленное к центру Земли:
G = т g
где g = 9,81 м/с2 - ускорение свободного падения.
Третья аксиома (третий закон Ньютона)
Силы взаимодействия двух тел равны по величине и направлены по одной прямой в разные стороны:

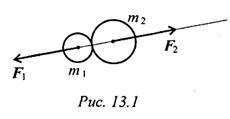
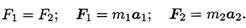
Откуда m1a1 = m2a2 или
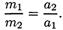
При взаимодействии ускорения обратно пропорциональны массам.
Четвертая аксиома (закон независимости действия сил)
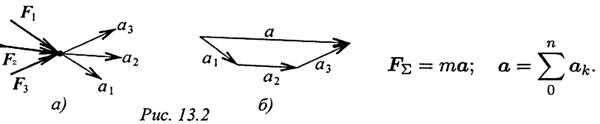
Ускорение, сообщаемое точке системой сил, равно геометрической сумме ускорений, сообщенных точке каждой силой в отдельности :

Дата добавления: 2017-10-04; просмотров: 3840;











