Кинематика поступательного движения материальной точки

Элементы кинематики поступательного и вращательного движения материальной точки

В физике, даже называя некий конкретный объект его собственным именем – автомобиль, электрон, поезд – мы все равно подразумеваем некоторую модель. Вообще в науке моделью называется абстрактная система, являющаяся упрощенной копией исследуемой реальной физической системы.

В разделе “механика” применяются две основные модели: материальная точкаиабсолютно твердое тело.

Материальной точкойиличастицей называется тело в тех случаях, когда изучается только поступательное движение тела как целого, при условии, что размеры, форма и другие его структурные свойства, а также протекающие в нем процессы в пределах точности измерений не влияют на движение тела.

При учете размера тела его можно принимать за материальную точку при соотношении величин r/h < 0,1%, где r – размер тела, а h – длина траектории его движения. Например, движение огромной Земли (диаметр > 12 тысяч км) вокруг Солнца можно рассматривать как движение материальной точки, т.к. расстояние Солнце – Земля достигает 150 миллионов км. В сравнении с Землей материальными точками являются огромные корабли и самолеты, да и каждый из нас – людей.

Когда рассматривается вращение тела вокруг какой-либо оси, проходящей через это тело, то применяют модель абсолютно твердого тела. Абсолютно твердымназывается физическое тело в тех случаях, когда его отдельные части остаются неподвижными друг относительно друга.

Кинематика поступательного движения материальной точки

Движение материи интуитивно означает перемещение в пространстве и времени. Но понятие перемещения имеет определенное содержание только при указании, относительно каких именно тел перемещается рассматриваемый объект или материальная точка. В этом заключается фундаментальное свойство природы, состоящее в том, что всякое движение относительно.

В кинематике причины (силы), вызывающие движение, не рассматриваются. Основным понятием кинематики является понятие системы отсчета. Системой отсчета называется совокупность тел, по отношению к которым рассматривается движение, и прибора для отсчета времени (часов), неподвижного относительно тел отсчета.

Опытным фактом для человека является трехмерность мирового пространства и его эвклидовость на расстояниях, малых по сравнению с радиусом кривизны Вселенной (~ 10²⁶ м). Поэтому очень часто систему отсчета изображают трехмерной прямоугольной «декартовой» системой координат, оси которой жестко связаны с набором тел образующих совместно с неподвижными относительно них часами систему отсчета (такие часы обозначают как t в кружке, рис.2.1.). Начало координат О “привязывают” к телу отсчета, движущемуся или

неподвижному.

z t

0 х

y

Рисунок 1.1 Прямоугольная система координат с неподвижными относительно неё часами

В некоторых случаях более удобными являются системы координат цилиндрической или сферической симметрии. Тогда вместо набора (x,y,z) используются наборы (r,x,q) или (r,q,j) – радиус, координату линейную или угловую. Путем математических преобразований пересчитать координаты точки в любую из этих систем координат.

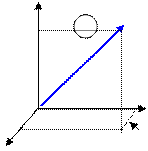
Положение материальной точки в пространстве однозначно определяется 3-мя координатами (x,y,z) по отношению к системе отсчета с прямоугольной системой координат. Однако чаще положение частицы описывается радиус-вектором 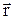(рис. 1.2).

z

z _M t · M

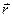
O x

y x_M y_M

Рисунок 1.2 К определению понятия радиус-вектора

Радиус-векторомназывается вектор, начинающийся в начале координат О и заканчивающийся в описываемой точке, проекции которого на оси координат системы отсчета равны координатам x,y,z.

Используется параметрическая форма записи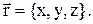

Число степеней свободы физической системы.Описать движение физической системы – значит в каждый момент времени указать положение всех её частей в пространстве по отношению к выбранной системе отсчета. Для этого необходимо задать некоторое количество параметров.