Скорость мгновенная и средняя.
Линейная скоростьявляется величиной, характеризующей быстроту изменения положения тела в пространстве.
Мгновенная скорость –скорость точкив данный момент времени есть первая производная радиус-вектора по времени
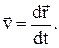
Из свойств производной следует, что при криволинейной траектории в любой момент времени мгновенная скорость направлена по касательной к траектории.
Скорость может быть представлена через проекции вектора
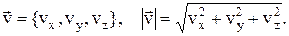
Изменение проекций вектора скорости также можно вычислить:
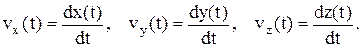
Широко применяются понятия векторная средняя скорость 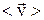 и скалярная средняя путевая скорость <v>пут.
и скалярная средняя путевая скорость <v>пут.
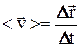
есть вектор коллинеарный вектору 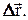 Он показан как vср на рис.1.3.
Он показан как vср на рис.1.3.
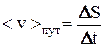 ,
,
где DS – длина всего пройденного за время Dt пути.
Ускорение.
Ускорение есть мера изменения скорости во времени:
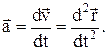
Естественно эту величину, так же как скорость, можно представить в виде проекций скорости и радиус-вектора:
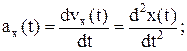
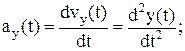
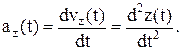
Величина мгновенной скорости при равнопеременном движении может быть найдена из известного соотношения
Vt=V0±at.
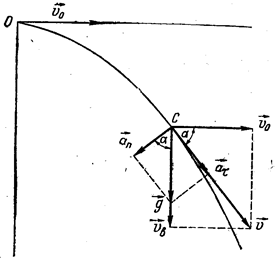
В достаточно общем случае криволинейного движения на плоскости ускорение может иметь как проекцию в направлении движения – касательную аt, – так и перпендикулярную ей нормальную или центростремительную аn составляющую (рис.1.4).
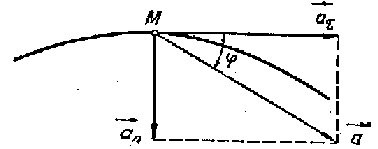 |
Рисунок 1.4 Ускорения при криволинейном движении
Тангенциальное ускорение есть проекция вектора полного ускорения на касательную к траектории, на направление вектора скорости и характеризует быстроту изменения величины скорости (её модуля). По величине 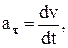 сонаправлено с
сонаправлено с 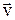 , при равноускоренном движении направлено так же, как и v, при равнозамедленном направлено противоположно
, при равноускоренном движении направлено так же, как и v, при равнозамедленном направлено противоположно 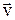 .
.
Нормальное ускорение есть проекция полного ускорения на направление, перпендикулярное 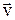 , характеризует быстроту изменения положения вектора
, характеризует быстроту изменения положения вектора 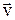 в пространстве и по величине равно
в пространстве и по величине равно 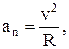 где R – радиус кривизны траектории в данной её точке.
где R – радиус кривизны траектории в данной её точке.
Очевидно, что
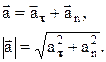
Особо интересен случай движение тела в поле силы тяжести. В этом случае полное ускорение постоянно равно g – ускорению свободного падения, независимо от формы траектории.
Так, например, если тело брошено горизонтально с какой-то башни (рис.1.5), то легко по рисунку понять, что есть тангенциальное и нормальное ускорения и как они связаны с соответствующими проекциями 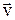 . Естественно, если сопротивление воздуха не учитывается, то сохраняется величина горизонтальной составляющей скорости V0=Vx, а вертикальная составляющая растет по закону Vy =gt.
. Естественно, если сопротивление воздуха не учитывается, то сохраняется величина горизонтальной составляющей скорости V0=Vx, а вертикальная составляющая растет по закону Vy =gt.
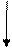
 х
х
y
Рисунок 1.5. Движение тела, брошенного горизонтально
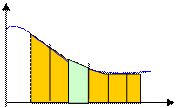
Величина пройденного телом пути является важнейшей практической характеристикой, вычисление которой зависит от вида движения: равномерное, равнопеременное, неравномерное. На рис. 1.6 а,б,в представлены графики зависимостей V=V(t) для этих видов движения.

 V=const V=Vo+at V=V(t) Vi
V=const V=Vo+at V=V(t) Vi
 V V V D Si
V V V D Si





 at1 Dti
at1 Dti




 S Vo S S
S Vo S S

O t1 t2 t O t1 t O t1 t2 t
a) б) в)
Рис.1.6 Графики V=V(t) при равномерном (а), равнопеременном (б) и неравномерном движениях (в)
Поскольку путь представляет собой графически площадь фигуры под графиком зависимости V=V(t), то при равномерном движении (рисунок 1.6 а) путь, пройденный в интервале времени (t2 - t1) просто численно равен площади прямоугольника
S = V×Dt = V(t2 –t1).
При равноускоренном движении (рисунок 1.6 б) аналогично путь равен площади трапеции, которую можно определить двумя способами:
1) как сумму площадей прямоугольника и треугольника:
S = Sð + SÑ = Vot1+;
2) по средней линии трапеции (выделена на рис.1.6.б красным цветом)
S = <V>t1 = 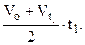
Следует заметить, что приведенный способ определения средней скорости применим лишь при равнопеременном движении.
Если скорость в зависимости от времени изменяется каким-то сложным образом, зачастую не описываемым простыми функциями, то путь вычисляется как сумма, складывающаяся из элементов Vi×Dti (см. рис.1.6,в, выделено светло-зеленым цветом), в пределах каждого из которых скорость можно полагать постоянной
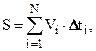
где N – число разбиений в интервале времени t1 – t2.
Если вид функции V(t) достаточно прост и интегрируем, то
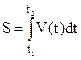 .
.
Дата добавления: 2017-10-04; просмотров: 1222;











