Кривая второго порядка может быть задана уравнением

Ах² + 2Вху + Су² + 2Dx + 2Ey + F = 0.

Существует система координат (не обязательно декартова прямоугольная), в которой данное уравнение может быть представлено в одном из видов, приведенных ниже.

1) 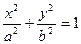- уравнение эллипса.

2) 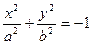- уравнение “мнимого” эллипса.

3) 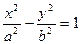- уравнение гиперболы.

4) a²x² – c²y² = 0 – уравнение двух пересекающихся прямых.

5) y² = 2px – уравнение параболы.

6) y² – a² = 0 – уравнение двух параллельных прямых.

7) y² + a² = 0 – уравнение двух “мнимых” параллельных прямых.

8) y² = 0 – пара совпадающих прямых.

9) (x – a)² + (y – b)² = R² – уравнение окружности.

Окружность.

В окружности (x – a)² + (y – b)² = R² центр имеет координаты (a; b).

Эллипс.

Определение. Эллипсом называется линия, заданная уравнением .

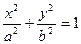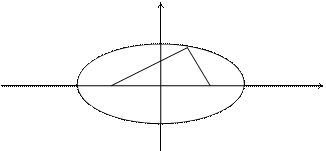
Определение. Фокусаминазываются такие две точки, сумма расстояний от которых до любой точки эллипса есть постоянная величина.

у

М

r₁

r₂

F₁ O F₂ х

F₁, F₂ – фокусы. F₁ = (c; 0); F₂(-c; 0)

с – половина расстояния между фокусами;

a – большая полуось;

b – малая полуось.

Теорема. Фокусное расстояние и полуоси эллипса связаны соотношением:

a² = b² + c².

Определение. Форма эллипса определяется характеристикой, которая является отношением фокусного расстояния к большей оси и называется эксцентриситетом.

Е = с/a.

Т.к. с < a, то е < 1.

Определение. Величина k = b/a называется коэффициентом сжатияэллипса, а величина 1 – k = (a – b)/a называется сжатиемэллипса.

Коэффициент сжатия и эксцентриситет связаны соотношением: k² = 1 – e².

Если a = b (c = 0, e = 0, фокусы сливаются), то эллипс превращается в окружность.

Если для точки М(х₁, у₁) выполняется условие: 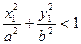, то она находится внутри эллипса, а если 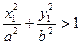, то точка находится вне эллипса.

Теорема. Для произвольной точки М(х, у), принадлежащей эллипсу верны соотношения:

r₁ = a – ex, r₂ = a + ex.

Теорема. Для того, чтобы точка лежала на эллипсе, необходимо и достаточно, чтобы отношение расстояния до фокуса к расстоянию до соответствующей директрисы равнялось эксцентриситету е.

Гипербола.

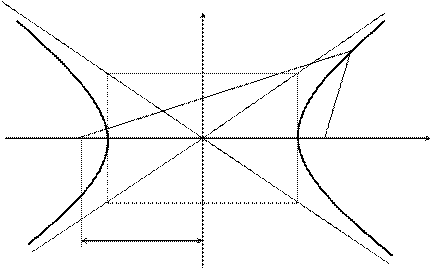
Определение. Гиперболойназывается множество точек плоскости, для которых модуль разности расстояний от двух данных точек, называемых фокусами есть величина постоянная, меньшая расстояния между фокусами.

y

M(x, y)

b

r₁

r₂

x

F₁ a F₂

c

По определению ïr₁ – r₂ï= 2a. F₁, F₂ – фокусы гиперболы. F₁F₂ = 2c.

Выберем на гиперболе произвольную точку М(х, у). Тогда:

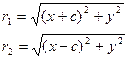
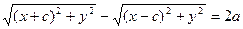
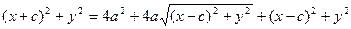
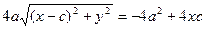
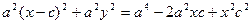
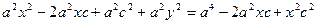
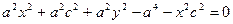
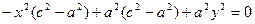
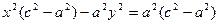
обозначим с² – а² = b² (геометрически эта величина – меньшая полуось)

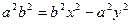
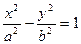
Получили каноническое уравнение гиперболы.

Гипербола симметрична относительно середины отрезка, соединяющего фокусы и относительно осей координат.

Ось 2а называется действительной осью гиперболы.

Ось 2b называется мнимой осью гиперболы.

Гипербола имеет две асимптоты, уравнения которых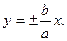

Определение. Отношение 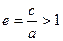называется эксцентриситетом гиперболы, где с – половина расстояния между фокусами, а – действительная полуось.

С учетом того, что с² – а² = b²:

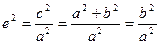
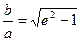
Если а = b, e = 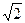, то гипербола называется равнобочной (равносторонней).

Определение. Две прямые, перпендикулярные действительной оси гиперболы и расположенные симметрично относительно центра на расстоянии a/e от него, называются директрисами гиперболы. Их уравнения: .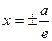

Теорема. Если r – расстояние от произвольной точки М гиперболы до какого- либо фокуса, d – расстояние от той же точки до соответствующей этому фокусу директрисы, то отношение r/d – величина постоянная, равная эксцентриситету.

Парабола.

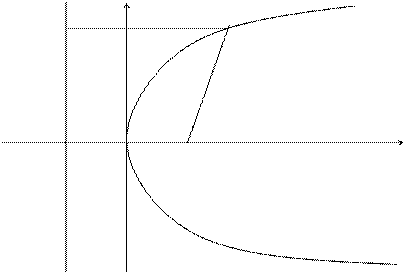
Определение. Параболой называется множество точек плоскости, каждая из которых находится на одинаковом расстоянии от данной точки, называемой фокусом, и от данной прямой, называемой директрисой и не проходящей через фокус.

Расположим начало координат посередине между фокусом и директрисой.

у

А М(х, у)

О F x

p/2 p/2

Величина р (расстояние от фокуса до директрисы) называется параметромпараболы. Выведем каноническое уравнение параболы.

Из геометрических соотношений: AM = MF; AM = x + p/2;

MF² = y² + (x – p/2)²

(x + p/2)² = y² + (x – p/2)²

x² +xp + p²/4 = y² + x² – xp + p²/4

y² = 2px

Уравнение директрисы: x = -p/2.

Системы координат.

Любая точка на плоскости может быть однозначно определена при помощи различных координатных систем, выбор которых определяется различными факторами. Способ задания начальных условий для решения какой – либо конкретной технической задачи может определить выбор той или иной системы координат. Для удобства проведения вычислений часто предпочтительнее использовать системы координат, отличные от декартовой прямоугольной системы. Кроме того, наглядность представления окончательного ответа зачастую тоже сильно зависит от выбора системы координат. Ниже рассмотрим некоторые наиболее часто используемые системы координат.

Полярная система координат.

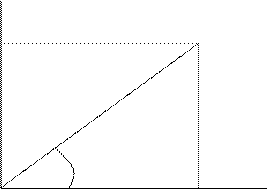
Определение. Точка О называется полюсом, а луч l – полярной осью.

Суть задания какой- либо системы координат на плоскости состоит в том, чтобы каждой точке плоскости поставить в соответствие пару действительных чисел, определяющих положение этой точки на плоскости. В случае полярной системы координат роль этих чисел играют расстояние точки от полюса и угол между полярной осью и радиус– вектором этой точки. Этот угол j называется полярным углом.

М

r

r =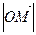

j

l

Можно установить связь между полярной системой координат и декартовой прямоугольной системой, если поместить начало декартовой прямоугольной системы в полюс, а полярную ось направить вдоль положительного направления оси Ох.

Тогда координаты произвольной точки в двух различных системах координат связываются соотношениями:

x = rcosj; y = rsinj; x² + y² = r²

Аналитическая геометрия в пространстве.

Уравнение линии в пространстве.

Как на плоскости, так и в пространстве, любая линия может быть определена как совокупность точек, координаты которых в некоторой выбранной в пространстве системе координат удовлетворяют уравнению:

F(x, y, z) = 0.

Это уравнение называется уравнением линии в пространстве.

Кроме того, линия в пространстве может быть определена и иначе. Ее можно рассматривать как линию пересечения двух поверхностей, каждая из которых задана каким- либо уравнением.

Пусть F(x, y, z) = 0 и Ф(x, y, z) = 0 – уравнения поверхностей, пересекающихся по линии L.

Тогда пару уравнений

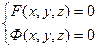
назовем уравнением линии в пространстве.