Пусть заданы векторы в прямоугольной системе координат
Как было сказано выше, матричный метод и метод Крамера применимы только к тем системам линейных уравнений, в которых число неизвестных равняется числу уравнений. Далее рассмотрим произвольные системы линейных уравнений.
Определение. Система m уравнений с n неизвестными в общем виде записывается следующим образом:
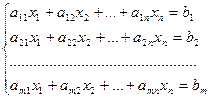 , (1)
, (1)
где aij – коэффициенты, а bi – постоянные. Решениями системы являются n чисел, которые при подстановке в систему превращают каждое ее уравнение в тождество.
Определение. Если система имеет хотя бы одно решение, то она называется совместной. Если система не имеет ни одного решения, то она называется несовместной.
Определение. Система называется определенной, если она имеет только одно решение и неопределенной, если более одного.
Определение. Для системы линейных уравнений вида (1) матрица
А = 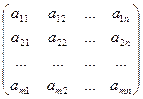 называется матрицей системы, а матрица
называется матрицей системы, а матрица
А*= 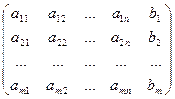 называется расширенной матрицей системы
называется расширенной матрицей системы
Определение. Если b1, b2, …,bm = 0, то система называется однородной. однородная система всегда совместна.
Элементарные преобразования систем.
К элементарным преобразованиям относятся:
1)Прибавление к обеим частям одного уравнения соответствующих частей другого, умноженных на одно и то же число, не равное нулю.
2)Перестановка уравнений местами.
3)Удаление из системы уравнений, являющихся тождествами для всех х.
Теорема Кронекера – Капелли.
(условие совместности системы)
(Леопольд Кронекер (1823-1891) немецкий математик)
Теорема:Система совместна (имеет хотя бы одно решение) тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы.
RgA = RgA*.
Очевидно, что система (1) может быть записана в виде:
x1 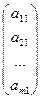 + x2
+ x2 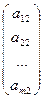 + … + xn
+ … + xn 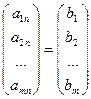
Метод Гаусса.
В отличие от матричного метода и метода Крамера, метод Гаусса может быть применен к системам линейных уравнений с произвольным числом уравнений и неизвестных. Суть метода заключается в последовательном исключении неизвестных.
Рассмотрим систему линейных уравнений:
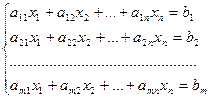
Разделим обе части 1–го уравнения на a11 ¹ 0, затем:
1) умножим на а21 и вычтем из второго уравнения
2) умножим на а31 и вычтем из третьего уравнения
и т.д.
Получим:
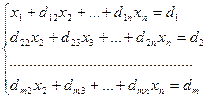 , где d1j = a1j/a11, j = 2, 3, …, n+1.
, где d1j = a1j/a11, j = 2, 3, …, n+1.
dij = aij – ai1d1j i = 2, 3, … , n; j = 2, 3, … , n+1.
Далее повторяем эти же действия для второго уравнения системы, потом – для третьего и т.д.
Элементы векторной алгебры.
Определение. Вектором называется направленный отрезок (упорядоченная пара точек). К векторам относится также и нулевой вектор, начало и конец которого совпадают.
Определение. Длиной (модулем) вектора называется расстояние между началом и концом вектора.
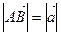
Определение. Векторы называются коллинеарными, если они расположены на одной или параллельных прямых. Нулевой вектор коллинеарен любому вектору.
Определение. Векторы называются компланарными, если существует плоскость, которой они параллельны.
Коллинеарные векторы всегда компланарны, но не все компланарные векторы коллинеарны.
Определение. Векторы называются равными, если они коллинеарны, одинаково направлены и имеют одинаковые модули.
Всякие векторы можно привести к общему началу, т.е. построить векторы, соответственно равные данным и имеющие общее начало. Из определения равенства векторов следует, что любой вектор имеет бесконечно много векторов, равных ему.
Определение. Линейными операциями над векторами называется сложение и умножение на число.
Определение.
1) Базисом в пространстве называются любые 3 некомпланарных вектора, взятые в определенном порядке.
2) Базисом на плоскости называются любые 2 неколлинеарные векторы, взятые в определенном порядке.
3)Базисом на прямой называется любой ненулевой вектор.
Определение. Если 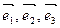 - базис в пространстве и
- базис в пространстве и 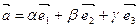 , то числа a, b и g - называются компонентами или координатами вектора
, то числа a, b и g - называются компонентами или координатами вектора 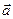 в этом базисе.
в этом базисе.
В связи с этим можно записать следующие свойства:
- равные векторы имеют одинаковые координаты,
- при умножении вектора на число его компоненты тоже умножаются на это число,
- при сложении векторов складываются их соответствующие компоненты.
Линейная зависимость векторов.
Определение. Векторы 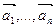 называются линейно зависимыми, если существует такая линейная комбинация
называются линейно зависимыми, если существует такая линейная комбинация 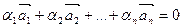 , при не равных нулю одновременно ai , т.е.
, при не равных нулю одновременно ai , т.е. 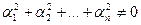 .
.
Если же только при ai = 0 выполняется 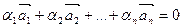 , то векторы называются линейно независимыми.
, то векторы называются линейно независимыми.
Система координат.
Для определения положения произвольной точки могут использоваться различные системы координат. Положение произвольной точки в какой- либо системе координат должно однозначно определяться. Понятие системы координат представляет собой совокупность точки начала отсчета (начала координат) и некоторого базиса. Как на плоскости, так и в пространстве возможно задание самых разнообразных систем координат. Выбор системы координат зависит от характера поставленной геометрической, физической или технической задачи. Рассмотрим некоторые наиболее часто применяемые на практике системы координат.
Декартова система координат.
Зафиксируем в пространстве точку О и рассмотрим произвольную точку М.
Вектор 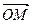 назовем радиус- вектором точки М. Если в пространстве задать некоторый базис, то точке М можно сопоставить некоторую тройку чисел – компоненты ее радиус- вектора.
назовем радиус- вектором точки М. Если в пространстве задать некоторый базис, то точке М можно сопоставить некоторую тройку чисел – компоненты ее радиус- вектора.
Определение. Декартовой системой координат в пространстве называется совокупность точки и базиса. Точка называется началом координат. Прямые, проходящие через начало координат называются осями координат.
1-я ось – ось абсцисс
2-я ось – ось ординат
3-я ось – ось апликат
Чтобы найти компоненты вектора нужно из координат его конца вычесть координаты начала.
Если заданы точки А(x1, y1, z1), B(x2, y2, z2), то 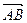 = (x2 – x1, y2 – y1, z2 – z1).
= (x2 – x1, y2 – y1, z2 – z1).
Определение. Базис называется ортонормированным, если его векторы попарно ортогональны и равны единице.
Определение. Декартова система координат, базис которой ортонормирован называется декартовой прямоугольной системой координат.
Длина вектора в координатах определяется как расстояние между точками начала и конца вектора. Если заданы две точки в пространстве А(х1, y1, z1), B(x2, y2, z2), то 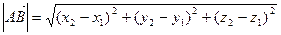 .
.
Если точка М(х, у, z) делит отрезок АВ в соотношении l/m, то координаты этой точки определяются как:
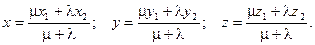
В частном случае координаты середины отрезка находятся как:
x = (x1 + x2)/2; y = (y1 + y2)/2; z = (z1 + z2)/2.
Линейные операции над векторами в координатах.
Пусть заданы векторы в прямоугольной системе координат
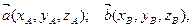 тогда
тогда
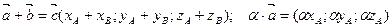
Скалярное произведение векторов.
Определение. Скалярным произведениемвекторов 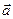 и
и 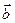 называется число, равное произведению длин этих сторон на косинус угла между ними.
называется число, равное произведению длин этих сторон на косинус угла между ними.

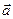 ×
× 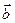 = ï
= ï 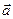 ïï
ïï 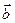 ïcosj
ïcosj
Если рассматривать векторы 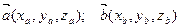 в декартовой прямоугольной системе координат, то
в декартовой прямоугольной системе координат, то

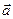 ×
× 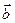 = xa xb + ya yb + za zb;
= xa xb + ya yb + za zb;
 Используя полученные равенства, получаем формулу для вычисления угла между векторами:
Используя полученные равенства, получаем формулу для вычисления угла между векторами:
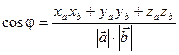 ;
;
Векторное произведение векторов.
Определение. Векторным произведениемвекторов 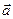 и
и 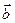 называется вектор
называется вектор 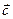 , удовлетворяющий следующим условиям:
, удовлетворяющий следующим условиям:
1) 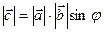 , где j - угол между векторами
, где j - угол между векторами 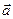 и
и 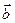 ,
,
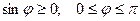
2) вектор 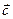 ортогонален векторам
ортогонален векторам 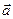 и
и 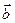
3) 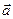 ,
, 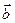 и
и 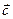 образуют правую тройку векторов.
образуют правую тройку векторов.
Обозначается: 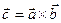 или
или 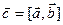 .
.
 |
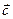
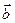
j
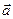

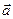 ´
´ 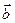 =
= 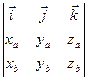
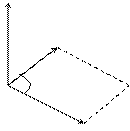
6) Геометрическим смыслом векторного произведения векторов является площадь параллелограмма, построенного на векторах 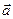 и
и 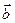 .
.
Смешанное произведение векторов.
Определение. Смешанным произведением векторов 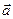 ,
, 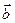 и
и 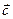 называется число, равное скалярному произведению вектора
называется число, равное скалярному произведению вектора 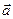 на вектор, равный векторному произведению векторов
на вектор, равный векторному произведению векторов 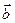 и
и 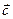 .
.
Обозначается 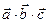 или (
или ( 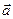 ,
, 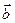 ,
, 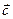 ).
).
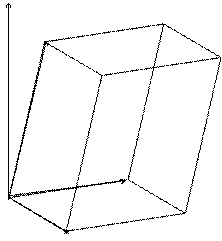
Смешанное произведение 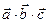 по модулю равно объему параллелепипеда, построенного на векторах
по модулю равно объему параллелепипеда, построенного на векторах 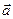 ,
, 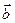 и
и 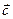 .
.
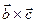
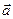
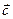
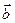
Уравнение поверхности в пространстве.
Определение. Любое уравнение, связывающее координаты x, y, z любой точки поверхности является уравнением этой поверхности.
Общее уравнение плоскости.
 Определение. Плоскостьюназывается поверхность, вес точки которой удовлетворяют общему уравнению:
Определение. Плоскостьюназывается поверхность, вес точки которой удовлетворяют общему уравнению:
Ax + By + Cz + D = 0,
где А, В, С – координаты вектора 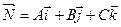 -вектор нормали к плоскости.
-вектор нормали к плоскости.
Возможны следующие частные случаи:
А = 0 – плоскость параллельна оси Ох
В = 0 – плоскость параллельна оси Оу
С = 0 – плоскость параллельна оси Оz
D = 0 – плоскость проходит через начало координат
А = В = 0 – плоскость параллельна плоскости хОу
А = С = 0 – плоскость параллельна плоскости хОz
В = С = 0 – плоскость параллельна плоскости yOz
А = D = 0 – плоскость проходит через ось Ох
В = D = 0 – плоскость проходит через ось Оу
С = D = 0 – плоскость проходит через ось Oz
А = В = D = 0 – плоскость совпадает с плоскостью хОу
А = С = D = 0 – плоскость совпадает с плоскостью xOz
В = С = D = 0 – плоскость совпадает с плоскостью yOz
Уравнение плоскости, проходящей через три точки.
Дата добавления: 2017-10-04; просмотров: 1560;











