Правила приведения к СКНФ.

Из определения СКНФ следует, что СКНФ обладает следующими свойствами совершенства (иными словами, СКНФ формулы F 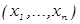называется её КНФ, удовлетворяющая следующим условиям):

а) в ней нет двух одинаковых множителей;

б) ни один множитель не содержит двух одинаковых слагаемых;

в) ни один множитель не содержит какую-нибудь переменную 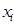вместе с её отрицанием ;

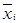г) каждый множитель содержит в качестве слагаемых все переменные 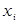или их отрицание 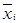, т.е. 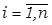для каждого множителя.

Можно доказать, что каждая не тождественно истинная формула имеет единственную (с точностью до порядка расположения множителей и слагаемых в множителях) СКНФ.

Правила приведения произвольной формулы к СКНФ аналогичны тем, которые описаны выше для нахождения СДНФ, и выражаются в двойственных терминах.

Пусть дана произвольная формула F .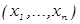

Проделаем несколько операций, которые приведут формулу к СКНФ.

1) Путем равносильных преобразований приведем формулу к КНФ.

2) Если в полученной КНФ какой-либо дизъюнктивный сомножитель В не содержит некоторую переменную 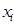(т.е. не удовлетворяет условию совершенства п. г)), то, используя равносильность 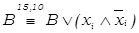, элементарную дизъюнкцию В заменяем на две элементарных дизъюнкции: 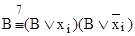, каждая из которых уже содержит переменную 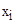- удовлетворили условию совершенства п. г).

3) Если в КНФ входят две одинаковых элементарных дизъюнкции В, то лишнюю отбрасываем, поскольку 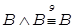- удовлетворили условию совершенства п. а).