Способ составления СНФ для произвольной формулы алгебры логики по таблице истинности.

Пример 1.

Пусть некоторая функция f трёх переменных задана следующей таблицей истинности:

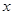
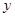
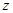
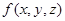
Проделаем следующие операции.

1) Выбираем наборы значений переменных, для которых :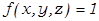

(0; 1; 1), (1; 0; 1), (1; 1; 0), (1; 1; 1).

2) Каждому из этих наборов сопоставляем (ставим в соответствие) конъюнкцию переменных 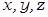или их отрицаний, принимающую при этих значениях переменных значение 1:

набору (0; 1; 1) – конъюнкцию ,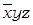

набору (1; 0; 1) – конъюнкцию ,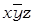

набору (1; 1; 0) – конъюнкцию ,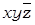

набору (1; 1; 1) – конъюнкцию .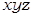

3) Дизъюнкция этих конъюнкций равна единице в тех и только тех случаях, когда и заданная функция принимает значение 1 и, следовательно, представляет собой одно из возможных выражений этой функции, т.е.

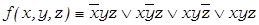Это выражение является, очевидно, СДНФ данной функции.

Пример 2

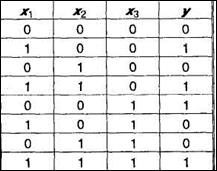
Пусть задана конкретная таблица истинности (табл. 1.10) для функции, зависящей от трех аргументов.

Тогда, выписывая соответствующие конъюнкты против единичных значений у, мы получим СДНФ. Если же мы выпишем дизъюнкты против нулевых значений у, то в результате уже получим СКНФ. Наконец, СПНФ образуется путем замены в СДНФ: v на + и 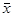на 1 + x.

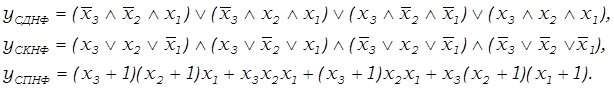
В последнем случае выражение для у_спнф легко можно упростить, если раскрыть скобки и взаимно сократить все одинаковые слагаемые, входящие в формулу четное число раз:

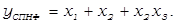
Подобное упрощение, которое называется минимизацией логической функции, можно осуществить и по отношению к СДНФ и СКНФ.

В логике Буля действует закон склеивания:

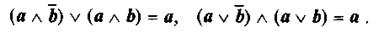
Применение этих законов позволяет найти более компактные аналитические выражения для заданной функции у, т.е. минимальную дизъюнктивную нормальную форму 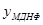. Приведем соответствующие формы представления функции у, заданной табл. 1.10:

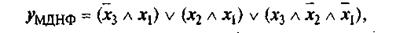
и для СКНФ. т.е. минимальную КНФ:

У_МКНФ=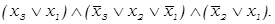

Контрольные вопросы.

1. Какие формы представления логических функций вы знаете?

2. На какую комбинацию областей можно разбить логическую функцию?

3. Сколько имеется логических операций?

4. Что называют таблицами истинности, для чего их используют?

5. Что называют конституентами?

6. Дайте понятие совершенной дизъюнктивной нормальной формы.

7. Дайте понятие совершенной конъюнктивной нормальной формы.

8. Дайте понятие совершенной полиномиальной нормальной формы.

9. Для чего используют совершенные нормальные формы?

10. Что значит минимизация логической функции?

Лекция № 6

Тема: «Введение в логику высказываний»

План лекции

1. Понятие высказывания

2. Замечания для логических связок

3. Различия между объектными и субъектными высказываниями

1. Под высказыванием мы будем понимать грамматически правильное повествовательное предложение, про которое можно сказать, что оно либо истинно, либо ложно, например:

«Киев — столица Украины»,

«Париж — столица России».

Первое высказывание является истинным, второе — ложным. Возьмем два простых высказывания:

А = «На улице идет дождь»,

В = «Над моей головой раскрыт зонтик».

С помощью пяти логических связок можно образовать следующие сложные высказывания:

1) отрицание:

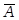= «На улице не идет дождь»;

2) дизъюнкция:

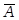v В = «На улице не идет дождь или над моей головой раскрыт зонтик»;

3) конъюнкция:

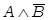= «На улице идет дождь и над моей головой не раскрыт зонтик»;

4) импликация:

А → В = «Если на улице идет дождь, то над моей головой раскрыт зонтик»;

5) эквивалентность:

В ~ А = «Над моей головой раскрыт зонтик тогда и только тогда, когда на улице идет дождь».

2. Другие логические связки, известные нам по логике Буля, в логике высказывания не используются. Теперь сделаем по поводу каждой из пяти указанных связок небольшие замечания.

Отрицание. Высказывание А по-другому можно прочитать так:

«Истинно то, что на улице идет дождь».

Поэтому, если А = 0 , то это означает, что на улице не идет дождь. Дополняющее высказывание 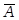также ориентируется на истинное высказывание, т.е. его следует понимать как

«Истинно то, что на улице не идет дождь».

Тогда 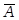= 1 будет обозначать ту же самую ситуацию, что и в предыдущем случае, т.е. отсутствие дождя.

Дизъюнкция. В нашем конкретном примере дизъюнкция двух высказываний 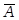и В, в принципе, может подразумевать и конъюнкцию этих же высказываний. Однако часто грамматический союз или не включает в себя союз и. Например,пусть будут даны два других высказывания:

P = «Петр находится в кинотеатре»

Q = «Петр находится в бассейне»

Если для нас не столь важно, где находится Петр, то мы, конечно, можем использовать союз или с включенным в него союзом и, формально записав:

Р v Q = «Петр находится в кинотеатре или/и в бассейне».

Но если нам нужно точно установить, где находится Петр, то мы обязаны исключить случай одновременного присутствия Петра в кинотеатре и бассейне, т.е. формально записать:

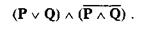
Подобные высказывания называются строгой дизъюнкцией, которая означает «либо Р, либо Q , но не Р и Q одновременно». И хотя, с точки зрения логики Буля, эта логическая операция равносильна операции симметрической разности:

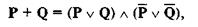
исторически сложилось так, что символ «+» в логике высказываний не используется.

Конъюнкция. Логический союз и необязательно должен представляться через грамматический союз и. В частности, выше приведенное выражение можно прочитать несколько иначе:

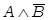= «На улице идет дождь, а над моей головой не раскрыт зонтик».

Союзы а и но по смыслу часто совпадают с союзом и, поэтому они используются в сложных конъюнктивных предложениях.

Однако языковая ситуация может стать такой, что союз и перестает играть роль конъюнкции; приведем два сложных предложения:

«Ему стало страшно и он убил человека»

«Он убил человека и ему стало страшно»

Здесь не коммутативность двух простых предложений очевидна, поскольку мы имеем дело со скрытой импликацией, когда одно простое предложение обусловливает другое.

Импликация. Высказывание типа «если А, то В» носит объясняющий характер. Оно как бы разъясняет нам, почему имеет место событие В — потому что имело место событие А. Это свойство импликации особенно ценно для логики высказываний.

Объясняющий характер импликации тесно связан с причинно-следственным отношением, при котором А выступает в роли причины, а В — следствия. Причинно-следственная связь между А и В грамматически может быть оформлена предложениями: «А является достаточным основанием для В», «В , потому что А», «В при условии выполнения А» и т.д. Если под А и В понимать прежние высказывания, то результат причинно-следственного отношения можно оформить следующей таблицей истинности (табл. 1). Вторая строка таблицы говорит об отсутствии причинно-следственного отношения между событиями А и В.

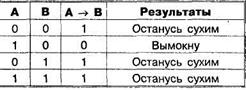
Эквивалентность. Высказывание «А эквивалентно В» может быть с успехом заменено на «А равно В», «А тождественно В», «А равносильно В», «А тогда и только тогда, когда В» и т.д. Так как эквивалентность выражается через конъюнкцию двух импликаций:

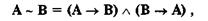
то это отношение часто возникает при одновременном выполнении двух условий: «из А следует В» и «из В следует А». Таким образом, при эквивалентности двух событий невозможно одному из них приписать роль только причины, а другому — только следствия. Например, два события:

R = «Нарастание анархии в обществе»,

S = «Падение авторитета власти»,

являются вполне равнопорядковыми событиями, поскольку причиной нарастания анархии в обществе является падение авторитета власти; и наоборот, падение авторитета власти происходит из-за нарастания анархии в обществе. В данной ситуации бессмысленно обвинять только власть в слабости и некомпетентности или обвинять народ в несознательности и недисциплинированности.

События R и S образуют логический круг; их будем называть сильно связанными событиями и выражать следующими тождественными формами:

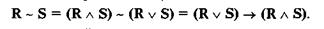
Понятие «сильной связанности» совпадает с понятием «эквивалентности», если речь идет о двух событиях. Но возьмем, к примеру, хорошо известное объяснение, на чем держится Земля:

Земля (X) держится на трех китах (Y), киты (Y) держатся на водах океана (Z), океан (Z) держится на Земле (X).

Последовательность, куда входят три названных объекта X , Y и Z, тоже образуют логический круг:

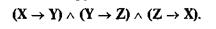
Однако отношение эквивалентности (быть взаимной опорой друг для друга) между всеми тремя объектами, т.е.

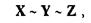
здесь не возникает, да и не могло возникнуть, так как мы ведь не утверждаем, что Земля является непосредственной опорой для китов (X ~ Y), или что киты являются непосредственной опорой для вод океана (Y ~ Z). Поэтому эквивалентность в данном случае проявляется в весьма своеобразной форме:

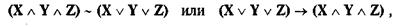
что можно истолковать в случае операции эквивалентности как: одновременное появление всех трех опор произойдет тогда и только тогда, когда возникнет хотя бы одна из опор, и наоборот; для операции импликации: если возникнет какая-нибудь одна из опор, то это приведет к появлению всех трех опор.

Таким образом, сильная связанность или логический круг есть нечто промежуточное между причинно-следственным отношением и отношением эквивалентности. Подобные отношения возникают очень часто, например, между членами преступной организации, где все связаны круговой порукой, и невозможно найти крайнего.

3. В заключение этого вводного подраздела хотелось бы подчеркнуть важность различия между языком и метаязыком, между объектными и субъектными высказываниями. Пренебрегая этим различием, мы рискуем впасть в противоречие, которое называется логическим парадоксом.

С древних времен известен так называемый «Парадокс лжеца». Изложим его суть.

«Я лжец», — сказал лжец.

Итак, некий лжец сообщает о себе, что он лжец. Следовательно, здесь он выступает в своем противоположном качестве, а именно — нелжеца. Поэтому приведенное высказывание на самом деле нужно понимать иначе:

«Я лжец», — сказал нелжец. *

Теперь получается, что правдивый человек сообщает о себе, что он лжец. Правдивому человеку мы, естественно, должны верить. Поэтому второе высказывание следует понимать все-таки так, как это отражено в первом высказывании. Таким образом, возникает неопределенность, заключающаяся в том, что непонятно, как квалифицировать говорящего — как лжеца или как нелжеца, т.е. непонятно, как идентифицировать высказывание — как истинное или как ложное.

Парадокс возник потому, что в приведенных высказываниях не делается разграничения между двумя принципиально различными логическими уровнями. Помимо «лжеца» или «нелжеца» в данной логической ситуации участвует субъект (метанаблюдатель). Если провести четкое синтаксическое отделение смыслового содержания, которое должно относиться к нам, как метанаблюдателям, от прочей семантики объектных персонажей, то логическое противоречие будет снято. Ситуацию с лжецом необходимо представлять следующим образом:

«Я лжец», — сказал лжец.

«Это истинно», — сказал метанаблюдатель.

«Я лжец», — сказал нелжец.

«Это ложно»,—сказал метанаблюдатель.

«Я нелжец», —сказал лжец.

«Это ложно», — сказал метанаблюдатель.

«Я нелжец», — сказал нелжец.

«Это истинно», — сказал метанаблюдатель.

ложно * ложно = истинно,

истинно * ложно = ложно,

ложно * истинно = ложно,

истинно * истинно = истинно.

Контрольные вопросы.

1. Что такое высказывание? Привести пример

2. Как образуется логическая связка «отрицание». Привести пример.

3. Как образуется логическая связка «дизъюнкция». Привести пример.

4. Как образуется логическая связка «конъюнкция». Привести пример.

5. Как образуется логическая связка «импликация». Привести пример.

6. Как образуется логическая связка «эквивалентность». Привести пример.

7. Какими союзами можно пользоваться в логике высказываний при описании «отрицания». Привести пример

8. Какими союзами можно пользоваться в логике высказываний при описании «отрицания». Какие имеются особенности в высказываниях. Привести пример

9. Какими союзами можно пользоваться в логике высказываний при описании «дизъюнкции». Какие имеются особенности в высказываниях. Привести пример

10. Какими союзами можно пользоваться в логике высказываний при описании «конъюнкции». Какие имеются особенности в высказываниях. Привести пример

11. Какими союзами можно пользоваться в логике высказываний при описании «импликации». Какие имеются особенности в высказываниях. Привести пример

12. Какими союзами можно пользоваться в логике высказываний при описании «эквивалентности». Какие имеются особенности в высказываниях. Привести пример

Лекция № 7

Тема: «Доказательства в логике высказываний»

План лекции

1. Различия в построении доказательств в логике высказываний и логике Буля.

2. Построение доказательств в логике высказываний

3. Методы доказательств в логике высказываний

1. Логика — это наука о способах доказательства. Выясним, в чем, собственно, состоит различие в построении доказательств в логике высказываний и логике Буля.

В булевой логике все доказательства строились на отношении эквивалентности. Даже если во множественных выражениях и фигурировало отношение включения, что является частным случаем отношения порядка, то его мы переводили в тождество. Две логические функции считались эквивалентными, если они давали на соответствующих наборах аргументов абсолютно одинаковые значения нулей и единиц. При использовании формальной записи логических выражений отдельные звенья цепи любого доказательства там были связаны через символ равенства «=». Отношение эквивалентности удовлетворяет трем законам

рефлексивности: А = А;

симметричности: если А = В , то В = А;

транзитивности: если А = В и В = С, то А = С.

В логике высказываний все доказательства строятся на отношении порядка, т.е. на отношении, которое существует между причиной и следствием. Здесь уже отдельные звенья цепи доказательства связаны символом импликации. Однако символ импликации « → » при логическом выводе мы будем заменять на символ « => », подобно тому, как в логике Буля используются два символа эквивалентности — « ~ » и « = ». Символ « ~ » является объектным, а « = » — субъектным. Таким образом, следует различать язык логики высказываний и метаязык исследователя. Во избежание путаницы введем еще два метасимвола: вместо объектной конъюнкции « Λ » будем использовать субъектный символ метаконъюнкции — « , », а вместо объектной дизъюнкции « v » — субъектную метадизъюнкцию « ; ». Тогда утверждение, которое требуется доказать, в логике высказываний оформляется в виде следующего причинно-следственного отношения:

Р₁, Р₂, ...,Р_п => С, (1)

где Р_i— посылка (причина), С — заключение (следствие). Читается: «Если посылки Р_1; Р₂, ..., Р_п истинны, то заключение С тоже истинно» или, по-другому: «Если причины P₁, Р₂,..., Р_п имели место, то будет иметь место и следствие С».

Чтобы не спутать объектное высказывание (предложение) с субъектным высказыванием, справедливость которого мы намереваемся установить, условимся предложения типа (1) называть клаузой (clause).

Клауза — это метапредложение, в котором использовано отношение порядка, оформленное через символ метаимпликации «=> ». Как и отношение эквивалентности, отношение порядка удовлетворяет трем законам —

рефлексивности: А => А;

антисимметричности: если А => В , то => ;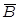

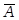транзитивности: если А => В и В => С, то А => С.

В отличие от эквивалентности отношение порядка предполагает выполнение закона антисимметричности, который можно записать так:

если А=>В и В=>А, то А = В.

Клауза есть именно формальная запись доказываемого предложения. Вместо букв в ней можно подставить объектные высказывания, и тогда клауза наполняется конкретным содержанием, которое уже именуется семантикой или легендой. Пример клаузы:

А → В, А=>В.

Если принять, что

А = сверкнула молния, В = грянул гром, то можно составить следующую легенду:

Известно, что если сверкнула молния, то после этого грянет гром. Молния сверкнула. Следовательно, должен и грянуть гром.

Ниже мы рассмотрим два метода доказательств справедливости логических клауз — аксиоматический метод, метод таблиц истинности. Как и в логике Буля, в логике высказываний существуют аксиоматический и конструктивный подходы доказательств логических выражений. Аксиоматическое построение логики высказываний состоит в том, чтобы попытаться вычленить из бесконечного числа истинных клауз независимую систему аксиом, с помощью которой можно было бы установить справедливость любых других клауз.

Логика высказывания является расширением логики Буля. Поэтому все истинные тождества логики Буля автоматически становятся справедливыми клаузами логики высказываний.

Таким образом, независимая система аксиом логики Буля, которая состоит из четырех законов — коммутативности, ассоциативности, дистрибутивности, нуля и единицы — автоматически становится системой аксиом и логики высказываний. Для выражения же отношения порядка, в принципе, требуется лишь какое-то одно элементарное высказывание, к которому можно было бы сводить все остальные более сложные высказывания. Сейчас мы его и введем.

Очевидная сентенция:

Истину может изречь всякий.

На формальном языке логики высказываний эту сентенцию можно представить следующей клаузой:

А =>В →А.

Она означает: «если А истинно, то источником этой истинности может быть что угодно, например В ». Если произвести эквивалентное преобразование этой клаузы

А, В =>А (2)

то семантика ее тоже изменится, и станет примерно такой: «если ранее было установлено, что А истинно, то истинность В не может проявиться так, что А станет ложным» или «истинность одного высказывания (В) не может повлиять на истинность другого высказывания (А)».

<2 3 456 7 8 >

Дата добавления: 2021-09-25; просмотров: 337;