Если водитель находился в комнате отдыха, то он должен был слышать все, что делается на складе
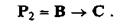
Если он имел возможность слышать, что делается на складе, то он слышал и выстрелы
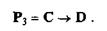
Если верить водителю, то он не слышал выстрелов
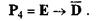
Заключение следователя:
Водитель меня обманывает при условии, что кассир говорит правду
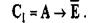
Кассир и водитель одновременно говорят правду
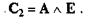
Формальная запись легенды:
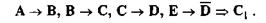
Доказать истинность следствия С1 аксиоматическим методом не составит труда. Для этого нужно воспользоваться тождеством:
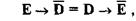
и затем трижды применить закон транзитивности. Заключение С2 ошибочно, так как
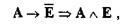
что означает
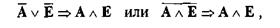
а это противоречит аксиоме порядка.
Теперь составим таблицу истинности (табл. 2), в которой под Р понимается обобщенная причина, т.е. конъюнкция всех Рi.
Таблица 2
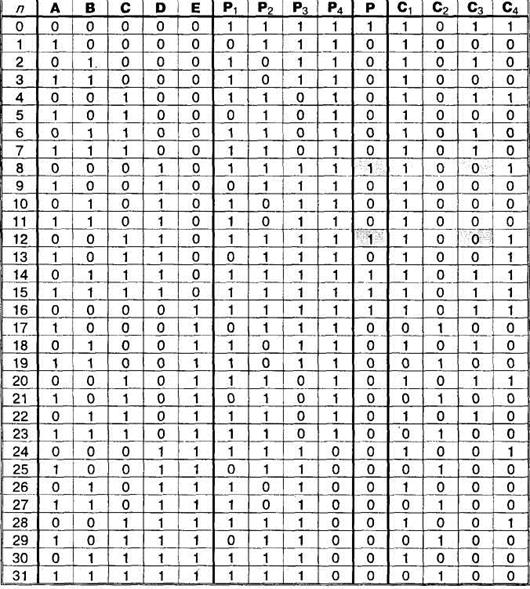
Клауза считается истинной, если единицы следствия (С) накрывают все единицы обобщенной причины (Р), т.е. единицы обобщенной причины образуют подмножество единиц следствия. Это требование выполняется для следствия С1 , но не для С2
Заключения C1 и С2, настолько очевидны, что никакой следователь в этом случае не стал бы прибегать к таблицам истинности. Но трудно найти такого следователя, который только путем одних рассуждений смог бы правильно выбрать из двух ниже представленных заключений истинное:
Водитель обманывает, он находился в комнате отдыха, а комната отдыха действительно расположена рядом со складом — все это так, но при условии, что кассир сказала правду или что водитель слышал выстрелы
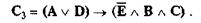
Водитель обманывает, он слышал выстрелы, а комната отдыха действительно расположена рядом со складом — все это так, но при условии, что кассир сказала правду или что водитель находился в комнате отдыха
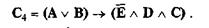
Единичные наборы для заключений С3 и С4 тоже приведены в табл.2. Для заключения С3 в строках 8 и 12 стоят нули, следовательно, условие причинно-следственного отношения не выполняется, и поэтому С3 является ложным заключением. Для заключения С4 все его единицы накрывают единицы обобщенной посылки Р. Следовательно, С4 является истинным заключением:
Истинность заключения тем очевиднее, чем большим числом его единиц накрываются единицы обобщенной причины.
Примеры.Составить легенды для приведенных ниже четырех клауз.
Клауза 1: А ~ С, С ~ Е, Е -> D, D → В => А → В.
А — Падение авторитета власти.
В — Политики, не способные управлять страной.
С — Нарастание анархии в обществе.
D — Высказывание абсурдных идей.
Е — Появление безответственных политиков.
«Падение авторитета власти происходит тогда и только тогда, когда нарастает анархия в обществе (А ~ С). Нарастание анархии в обществе равносильно появлению на политической арене безответственных политиков (С ~ Е). Появление подобных политиков приводит к тому, что они высказывают абсурдные идеи (Е → D). Высказывание политиками таких идей демонстрирует неспособность их управлять страной (D → В). Итак, падение авторитета власти приводит к появлению политиков, не способных управлять страной (А → В)».
Клауза 2: А -> В, В → Е, А → С, С → D, D → F, 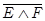 =>
=> 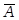 .
.
«Если человек занимается спортом (А), то он хочет быть здоровым (В). Хорошее здоровье (В) ведет к счастливой жизни (Е). Кроме того, если человек занимается спортом (А), то он, как правило, стремится достичь высоких спортивных результатов (С). Наличие высоких результатов (С) позволяет одерживать победы на соревнованиях (D). Победы на соревнованиях (D) влекут за собой всеобщее признание (F). Однако, человек не хочет жить счастливо и иметь всеобщее признание ( 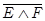 ). Значит, он не станет заниматься и спортом (
). Значит, он не станет заниматься и спортом ( 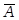 )».
)».
Клауза 3: J → Н, К → Н, I → J, Н → I, 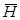 =>
=> 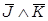 .
.
«Если знать язык программирования (J), то можно составить рабочую программу (Н). Рабочую программу можно также получить (Н) при условии наличия знакомого программиста (К). Овладеть языком программирования (J) можно, обучаясь в институте (I). Если программа работает (Н), то ее написал выпускник такого института (I). Но программа не работает ( 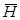 ). Это говорит о том, что желающий получить правильный результат не знает языка программирования (
). Это говорит о том, что желающий получить правильный результат не знает языка программирования ( 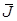 ) и не имеет знакомых программистов (
) и не имеет знакомых программистов ( 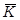 )».
)».
Клауза 4: А → В, С → D, В Λ D → Е, А, 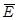 =>
=> 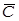 .
.
«Все живое способно чувствовать (А → В). Всякое материальное тело занимает определенный объем (С→D). Если нечто занимает пространственный объем и способно чувствовать, то это нечто есть ни что иное, как живой организм_(В Λ D → Е). Пусть существует нечто живое (А), но не являющееся организмом ( 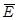 ). Тогда следует вывод, что это нечто нематериально (
). Тогда следует вывод, что это нечто нематериально ( 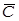 )».
)».
Выше приведены легенды. Запишем клаузы, отвечающие тексту или контексту этих легенд, для чего сформулируем необходимые посылки и два следствия: одно истинное, другое ложное. С помощью таблицы истинности найдем МНФ, минимальное и все трансверсальные покрытия (последнее задание выполнено только для варианта 21).
Для варианта 21 можно предложить следующую клаузу:
А ~ В, С → A, D → В, С → Е, Е => С → В.
А — Где-то что-то убыло.
В — Где-то что-то прибыло.
С — "Черная дыра " существует.
D — "Белая дыра " существует.
Е — Невозможность ничего увидеть.
«Если в одном месте что-то убудет, то в другом что-то непременно прибудет, и наоборот (А~ В). Если существует "черная дыра", то в нее все проваливается, то есть в ее окрестностях что-то убывает (С → А). Если существует "белая дыра", то из нее в окружающее пространство должно прибывать вещество (D → В). Если существует "черная дыра", то ее невозможно увидеть, так как она не излучает свет (С → Е). Астроном ничего не увидел (Е). Итак, "белая дыра" существует (D).» Это — ложное умозаключение. Истинным же заключением является, например, следующее: «Если существует "черная дыра", то где-то в пространстве вселенной должно непременно появляться вещество (С → В)».
Для варианта 22 можно составить следующую клаузу:
А → В, В → С, Е → ( 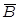 → D), D → F => (
→ D), D → F => ( 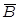
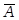 Λ Е) → F.
Λ Е) → F.
Введем следующие обозначения:
А — Возникновение перепада напряжения в сети.
В — Перегорание предохранителя.
С — Необходимость замены предохранителя.
D — Телевизор работает нормально.
Е — Телевизор подключен к сети питания.
F — Я смотрю "Новости".
«Если в сети был большой перепад напряжения, то сгорит предохранитель (А → В). Если предохранитель сгорел, необходима его замена (В → С). Если телевизор включен в сеть, то телевизор работает нормально при условии целостности предохранителя (Е → ( 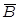 → D)). Если телевизор работает нормально, я увижу "Новости" (D → F). Я увижу "Новости" при условии отсутствия перепада напряжения и подключения телевизора к сети питания ((А л Е) -> F)». Данное следствие является ложным. Истинным же следствием будет: «Я увижу "Новости" при условии целостности предохранителя, отсутствия перепада напряжения в сети и подключения телевизора к сети питания (
→ D)). Если телевизор работает нормально, я увижу "Новости" (D → F). Я увижу "Новости" при условии отсутствия перепада напряжения и подключения телевизора к сети питания ((А л Е) -> F)». Данное следствие является ложным. Истинным же следствием будет: «Я увижу "Новости" при условии целостности предохранителя, отсутствия перепада напряжения в сети и подключения телевизора к сети питания ( 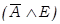 →F)».
→F)».
Для варианта 23 допустимо составить следующую простую клаузу:
А→В, В→С, C→D, D→E=>A→E.
А — Работа выполнена.
В — Отпуск на рыбалку.
С — Взять на рыбалку сына.
D — Рыбалку провести с лодкой.
Е — На рыбалку поедут все вместе.
«Если работа выполнена, то начальство отпустит на рыбалку (А → В). Если отпустят на рыбалку, то обязательно возьмут на нее и сына (В → С). Если берут сына, значит надо брать лодку (С → D). Если брать с собой лодку, то поедут все вместе (D → Е). Таким образом, если работа выполнена, то все вместе едут на рыбалку (А → Е)». Данное следствие является истинным. Ложным следствием является очевидно, такое: «Если работа сделана, то все вместе на рыбалку не едут (А → 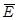 )».
)».
Для варианта 24 составим следующую клаузу:
А → (В Λ С), 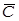 →
→ 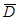 ,
, 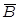 → (А → Е), D → (В v
→ (А → Е), D → (В v 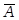 ) => (
) => ( 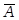 Λ В) → С.
Λ В) → С.
А — Уменьшение температуры.
В — Снижение давления.
С — Уменьшение объема.
D — Снижение скорости.
Е — Падение уровня.
«Уменьшение температуры приводит к снижению давления и уменьшению объема А → (В Λ С). Увеличение объема приводит к росту скорости потока (С → D). Повышение давления приводит к падению уровня, если при этом уменьшать температуру ( 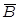 → (А → Е)) Снижение скорости приводит к уменьшению давлениями росту температуры (D → (В v
→ (А → Е)) Снижение скорости приводит к уменьшению давлениями росту температуры (D → (В v 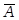 )). Технолог Иванов рассудил так: "Мне надо повысить давление при одновременном снижении скорости потока, поэтому я должен увеличить объем и температуру" ((
)). Технолог Иванов рассудил так: "Мне надо повысить давление при одновременном снижении скорости потока, поэтому я должен увеличить объем и температуру" (( 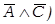 → (
→ ( 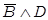 ))». Данное умозаключение является ложным. Истинным рассуждением будет, например, такое: «Уменьшение температуры и увеличение давления ведут к уменьшению объема ((
))». Данное умозаключение является ложным. Истинным рассуждением будет, например, такое: «Уменьшение температуры и увеличение давления ведут к уменьшению объема (( 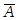 Λ В) → С)».
Λ В) → С)».
Для варианта 25 составим клаузу:
A v В v С, (С Λ D) → Е, (A v В) → 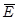 , С → D, => С → Е.
, С → D, => С → Е.
А — Надеть брезентовые штаны.
В — Надеть шерстяное платье.
С — Надеть пиджак и юбку с разрезом.
D — Взять с собой сумку.
Е — Великолепно смотрится.
«Я могу надеть на себя брезентовые штаны или шерстяное платье или пиджак и юбку с разрезом (A v В v С). Я буду выглядеть великолепно, если надену пиджак и юбку с разрезом и при этом возьму с собой сумку ((С Λ D) → Е). И наоборот, я буду выглядеть ужасно, если надену на себя брезентовые штаны или шерстяное платье ((A v В) → 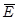 ). Однако сумку надо брать обязательно, если надеть пиджак и юбку с разрезом (С → D). Итак, чтобы выглядеть великолепно я выбираю последнее, т.е. надену на себя пиджак и юбку с разрезом (С → Е)». Данное заключение является истинным. Ложным может быть, например, такое: «Чтобы выглядеть великолепно, нужно надеть на себя брезентовые штаны (А → Е)».
). Однако сумку надо брать обязательно, если надеть пиджак и юбку с разрезом (С → D). Итак, чтобы выглядеть великолепно я выбираю последнее, т.е. надену на себя пиджак и юбку с разрезом (С → Е)». Данное заключение является истинным. Ложным может быть, например, такое: «Чтобы выглядеть великолепно, нужно надеть на себя брезентовые штаны (А → Е)».
Контрольные вопросы.
1. На чем строятся доказательства в логике высказываний в отличие от логики Буля?
2. Как оформляются утверждения в логике высказываний?
3. Закон рефлексивности. Пример
4. Закон антисимметричности. Пример
5. Закон транзитивности. Пример
6. Что такое клауза? Привести пример
7. Что предполагает аксиоматический метод доказательства высказываний?
8. Что предполагает конструктивный метод доказательства высказываний?
9. Основная аксиома логики высказываний
10. Что такое легенда? Привести пример
11. Аксиомы логики высказываний: отношения порядка, дистрибутивность.
12. Аксиомы логики высказываний: ассоциативность, коммутативность.
Лекция № 8
Тема: «Логика предикатов. Операции над предикатами
И кванторами»
План лекции
1. Понятие предиката
2. Функциональная природа предикатов
3. Кванторы
1. Проблема разрешимости — эта проблема ставится для формул исчисления предикатов, лишённых символов постоянных предметов и символов индивидуальных предикатов. В последующем изложении предполагается, что рассматриваемые формулы таковы (если не сделано специальных оговорок).
Каждая такая формула представляет собой определённое утверждение, истинное или ложное, когда оно относится к определённому полю M.
Если такая формула истинна для некоторого поля M и некоторых предикатов, на нём определённых, мы будем называть её выполнимой.
Если формула истинна для данного поля M и для всех предикатов, определённых на M, мы будем называть её тождественно истинной для поля M.
Если формула истинна для всякого поля M и для всяких предикатов, будем называть её тождественно истинной или просто истинной.
Формула называется ложной или невыполнимой, если ни для какого поля ни при каких замещениях предикатов она не является истинной. Легко показать, что если формула U тождественно истинна, то формула 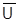 ложна, и наоборот.
ложна, и наоборот.
Постановка проблемы разрешимости для логики предикатов аналогична постановке этой проблемы для алгебры высказываний. Её решение и является целью данной курсовой работы. Итак, проблема ставится следующим образом: дать эффективный способ для определения — является ли данная формула выполнимой или нет.
Умея решать вопрос о выполнимости, мы тем самым сможем решать и вопрос об истинности любой формулы. В самом деле, если формула U истинна, то формула 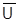 невыполнима, и обратно. Поэтому, доказав выполнимость или невыполнимость
невыполнима, и обратно. Поэтому, доказав выполнимость или невыполнимость 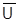 , мы тем самым проверим истинность U. Проблема разрешимости для логики предикатов является усилением проблемы разрешимости для исчисления высказываний, так как все формулы исчисления высказываний входят в число формул логики предикатов. Однако в то время как решение проблемы разрешимости для исчисления высказываний никаких трудностей не представляет, проблема разрешимости для логики предикатов оказалась связанной с серьёзными трудностями.
, мы тем самым проверим истинность U. Проблема разрешимости для логики предикатов является усилением проблемы разрешимости для исчисления высказываний, так как все формулы исчисления высказываний входят в число формул логики предикатов. Однако в то время как решение проблемы разрешимости для исчисления высказываний никаких трудностей не представляет, проблема разрешимости для логики предикатов оказалась связанной с серьёзными трудностями.
Современные исследования пролили свет на природу этих затруднений. В настоящее время представляется достаточно ясным, что решение этой проблемы в указанном смысле вообще невозможно. Иначе говоря, не может существовать никакого конструктивного правила, которое позволяло бы определять для любой формулы логики предикатов, является ли она тождественно истинной или нет. Для некоторых частных типов формул, однако, проблема разрешимости решается. Мы рассмотрим наиболее важный тип формул, для которых решение проблемы разрешимости может быть осуществлено, это формулы логики предикатов, зависящие от одного переменного.
Предикат — это функциональное высказывание, а высказывание — предикатная константа. Логика предикатов — это расширение логики высказываний за счет использования предикатов в роли логических функций. Эти функции несколько отличаются от функций, которые мы использовали в логике Буля. Булева функция однородна, т.е. для нее область значений функции и область изменений аргументов по типу одна и та же — логическая (либо истина, либо ложь). Для предикатов же область значений функции — логическая, а область изменений аргументов — предметная. Таким образом, эта функция — неоднородна. Приведем примеры предикатных функций.
Пусть имеется ряд простых высказываний:
P1 = «Иван читает Достоевского»,
Р2 = «Петр читает Достоевского»,
...........................................
Рп = «Степан читает Достоевского».
Вместо высказываний Р1; Р2,..., Рп мы могли бы ввести одноместный предикат Р(х), для которого переменная х принимала бы значения из предметной области —
х = {Иван, Петр, ... , Степан},
а сама предикатная функция передавалась бы словами:
P(х) = « х читает Достоевского».
Теперь изменим исходный ряд высказываний на другой:
P1 = «Иван читает Достоевского»,
Р2 = «Петр читает Толстого»,
......................................
Рп = «Степан читает Чехова».
Здесь можно было бы ввести уже двухместный предикат —
Р(х, у) = « х читает у »
с дополнительной предметной областью —
у= {Достоевский, Толстой, ... , Чехов}.
Введем трехместный предикат Р(х, у, z), который означает, что «х есть сумма у z». Допустим, в процессе вычислений переменная х приняла конкретное значение, равное 5. Тогда трехместный предикат превратится в двухместный:
Р(5, у, z) = «5 есть сумма у и z ».
При х = 5 и у = 3 получим одноместный предикат:
Р(5, 3, z) = « 5 есть сумма 3 и z ».
Наконец, если добавить условие z = 2 , то исходный предикат становится нульместным предикатом (константой или высказыванием), который в данном случае принимает истинное значение:
P1 = Р(5, 3, 2) = « 5 есть сумма 3 и 2 » = 1.
Но могло случиться, что z= 1 тогда имели бы ложное высказывание:
Ро = Р(5, 3, 1) = « 5 есть сумма 3 и 1 » = 0.
Таким образом, при замещении переменной хi, предметной постоянной аi, происходит превращение n-местного предиката P(x1 ,... ,xi... ,хn) в (n— 1) -местный — P(х1,... ,ai,... ,хn). Приписав конкретные значения всем аргументам предикатной функции — P(a1, ..., ai, ..., an), мы тем самым получаем предикатную константу, к которой применимы все законы логики высказываний.
2. Функциональная природа предиката влечет за собой введение еще одного понятия — квантора. Роль его выясним на следующих двух примерах:
1) «Все люди смертны. Сократ человек. Следовательно, Сократ смертен.»
2) «Некоторые люди гениальны. Сократ человек. Следовательно, Сократ гениален.»
Во втором примере хорошо чувствуется ложность заключения, поскольку интуитивно мы понимаем, что Сократ мог и не попасть в число гениальных людей.
Итак, ключевыми словами в наших примерах являются «все» и «некоторые». Когда какое-нибудь правило распространяется на всех индивидуумов, оно, естественно, распространяется и на Сократа. Когда же правило касается только некоторых, оно может оказаться в отношении Сократа как раз и неверным.
Термин «все х» обозначается в логике предикатов 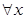 и называется квантором общности (символ
и называется квантором общности (символ 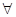 есть перевернутая буква А, которая является начальной буквой английского слова All — «все»). Термин «некоторые х» или «существует хотя бы одно значение х» обозначается через
есть перевернутая буква А, которая является начальной буквой английского слова All — «все»). Термин «некоторые х» или «существует хотя бы одно значение х» обозначается через 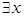 и называется квантором существования (символ
и называется квантором существования (символ 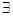 есть перевернутая буква Е, являющаяся первой буквой английского слова Exist — «существовать»).
есть перевернутая буква Е, являющаяся первой буквой английского слова Exist — «существовать»).
Выставляя кванторы перед предикатами, мы как бы усиливаем или ослабляем их действие. Так, выражение
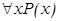
означает «для всех без исключения х свойство Р истинно», а выражение
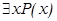
означает «существует по крайней мере одно значение х, для. которого свойство Р истинно». Мы не будем использовать так называемые свободные переменные, т.е. не будем рассматривать предикатные функции, аргументы которых не связаны ни квантором общности, ни квантором существования. Сказать «для всех х свойство Р истинно» — это все равно, что сказать «конъюнкция всех значений предикатной функции равна единице»:
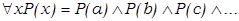
Квантор существования означает дизъюнкцию всех значений предикатной функции:
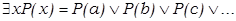
3. В логике предикатов вывод определяется так же, как и в исчислении высказываний и секвенции имеют тот же синтаксис. Аксиомы тоже определяются так же, как в логике высказываний. Все правила вывода логики высказываний – правила введения и удаления для пропозициональных связок, правила противоречия и сведения к противоречию – включены в множество правил вывода логики предикатов, с метапеременными для формул понимаемыми теперь как предикатные формулы. В дополнение, есть четыре новых правил вывода: правила введения и удаления для кванторов.
Предметное переменное, не связанное никаким квантором, мы будем называть свободным переменным.
Формулы, в которых из операций алгебры высказываний имеются только операции  ,
, 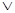 и
и 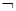 , а знаки отрицания относятся только к элементарным предикатам и высказываниям, будем называть приведёнными формулами.
, а знаки отрицания относятся только к элементарным предикатам и высказываниям, будем называть приведёнными формулами.
Приведённая формула называется нормальной, если она не содержит кванторов или если при образовании её из элементарных формул операции связывания квантором следуют за всеми операциями алгебры высказываний.
Если две формулы U и B, отнесённые к некоторому полю M, при всех замещениях переменных предикатов, переменных высказываний и свободных предметных переменных соответственно индивидуальными предикатами, определёнными на M, индивидуальными высказываниями и индивидуальными предметами из M, принимают одинаковые значения И или Л, то мы будем говорить, что эти формулы равносильны на поле M.
Если две формулы равносильны на любых полях M, то мы будем их называть просто равносильными.
Нормальную формулу, равносильную некоторой формуле U, мы будем называть нормальной формой формулы U.
Оба квантора можно отрицать и выражать один через другой на основе закона де Моргана:
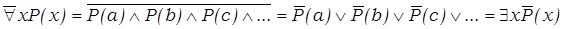
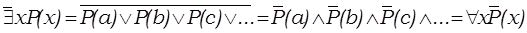
Отсюда
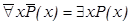
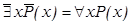
Контрольные вопросы.
1. Что такое предикат. Понятие логики предикатов. Привести пример
2. Что означает понятие «однородная функция», «неоднородная функция». Привести пример
3. Квантор общности. Что он означает? Привести пример
4. Что означает квантор общности?
5. Квантор существования. Привести пример
6. Что означает квантор существования?
7. Как можно выразить квантор существования через квантор общности?
8. Что такое одноместный, двухместный предикат. Привести пример
9. Что такое константа в логике предикатов? Привести пример
10. Что такое нульместный, трехместный предикат. Привести пример
11. Как можно выразить один квантор через другой
Лекция № 9
Тема: «Графы, орграфы, деревья. Операции над графами»
План лекции
План.
1. Графы, орграфы, деревья.
2. Матрицы смежности и инциденции
3. Операции над графами
Теория графов в последнее время широко используется в различных отраслях науки и техники, особенно в экономике и социологии.
Основы теории графов разработал Л. Эйлер, решавший задачу о разработке замкнутого маршрута движения по мостам в г. Кенигсберге. При решении задачи он обозначил каждую часть суши точкой, а каждый мост — линией, их соединяющей. В результате был получен граф (рис. 1).
Рис. 1
Эйлер доказал, что такая задача решения не имеет.
Быстрое развитие теория графов получила с созданием электронно-вычислительной техники, которая позволяла решить многие задачи алгоритмизации.
Пусть на плоскости задано некоторое множество вершин X и множество U соединяющих их дуг. Графом называют бинарное отношение множества X и множеств U: G =(X; U), или, иначе f: X → Y. Здесь f —отображение инциденции.
Рис. 2
Граф называется ориентированным, если указано направление дуг и неориентированным, если такое направление не указано. Примером неориентированного графа является карта дорог.
Граф называется петлей, если его начало и конец совпадают.
Две вершины называются смежными, если существует соединяющая их дуга.
Ребро иjназывается инцидентным вершине хi, если оно выходит или входит в вершину.
Степенью (валентностью) вершины называется число инцидентных ей ребер. Кратностью пары вершин называется число соединяющих их ребер или дуг.
Подграфом Ga графа G называется граф, в который входит лишь часть вершин графа G вместе с дугами их соединяющими.
Частным графом Gb графа называется граф, в который входит лишь часть дуг графа G вместе с вершинами их соединяющими. Карта шоссейных дорог это граф. Дороги Луганской области это подграф, а главные дороги — это частный граф.
Путем в графе G называется такая последовательность дуг, в которой конец каждой последующей дуги совпадает с началом предыдущей. Длиной пути называют число входящих в этот путь дуг. Путь может быть конечным и бесконечным. Путь, в котором никакая дуга не встречается дважды, называется элементарным.
Контур — это конечный путь, у которого начальная и конечная вершины совпадают. Контур называется элементарным, если все его вершины различны (кроме начальной и конечной). Контур единичной дуги называется петлей.
Дата добавления: 2021-09-25; просмотров: 581;











