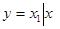Свойства счетных множеств.


Приведем свойства счетных множеств.

1°. Всякое подмножество счетного множества конечно или счетно.

2°. Сумма конечного или счетного числа конечных или счет­ных множеств есть конечное или счетное множество.

3°. Всякое бесконечное множество содержит счетное под­множество.

4°. Множество всех рациональных чисел счетно.

Докажем, например, свойство 2°. Пронумеруем сначала пер­вые элементы множеств, входящих в сумму, затем — вторые и т. д. Так как число элементов в каждом множестве конечно и число слагаемых в сумме также конечно, то таким образом мы получили новое счетное множество.

Остальные свойства доказываются аналогично.

3. Соотношения между множествами

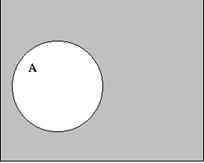
Включение (А ⊂ В). Множество А входит (включено) в множество В, или А является подмножеством В. Если всякий объект, обладающий свойством α, обладает также и свойством β, то говорят, что свойство α включает свойство β (α ⊃ β);

А ⊂ В↔ (а ∊ А→ a ∊ В).

Сумма (объединение) (AUВ). Объединение множеств А и В есть новое множество С, включающее в себя все элементы множеств А и В. Объект входит в множество С, если он входит в множество А или множество В. Сумме множеств соответствует сумма свойств, определяющих эти множества;

С = А U В = { ci/ci ∊ А или ci ∊ В}

Произведение (пересечение) (А ⋂ В). Пересечение множеств А и В есть новое множество С. Элементы множества С принадлежат множеству А (обладают его свойствами) и множеству В(обладают его свойствами). Произведению множеств соответствует произведение свойств, определяющих эти множества:

С = А ⋂ В = { ci/ci ∊ А и ci ∊ В}

Вычитание (А\В). Разность множеств А и В есть новое множество С, элементы которого обладают свойствами множества А и не обладают свойствами множества В или, что то же самое, принадлежат множеству А и не принадлежат множеству В:

С = А\В = { ci/ci ∊ А и ci ∉ В}

Дополнение ( 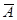). Если имеется некоторое «универсальное» множество U и все рассматриваемые множества есть его подмножества, элементами множества 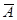являются все элементы, не входящие в А, но принадлежащие U:

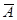={ аi/аi ∊ А }

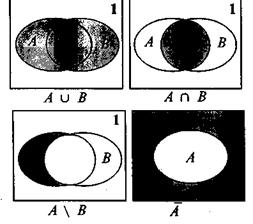
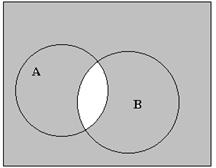
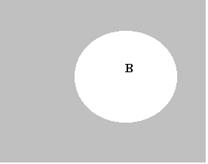
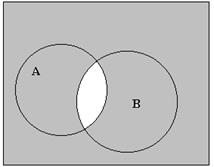
Множества часто задают графически с помощью диаграмм Эйлера—Венна, где всякий рассматриваемый контур соответствует одному из рассматриваемых множеств и ограничивает (символически) его элементы, а рамка, ограничивающая все элементы пространства, в верхнем правом углу имеет обозначение 1.

Введенные операции позволяют выражать одни множества через другие, при этом сначала выполняется операция дополнения, затем пересечения и потом объединения (вычитания). Для изменения этого порядка в выражении используют скобки.

На рисунке приведены диаграммы Эйлера, выражаю­щие основные соотношения между» множествами.

Прямое произведение А х В. Прямым произведением мно­жеств А и В называется множество М всех пар (а, Ь) таких, что a ∊ A, b ∊ В:

М = {(а, Ь)/а ∊ А, Ь∊ В}.

Если А = В, то такое произведение обозначают А2. Анало­гично можно ввести операцию прямого произведения мно­жеств А1, А2, ..., Ап, обозначаемую А1 х А2 х … х Ап. Здесь рассматриваются все векторы длины п. Если выполнено равенство А1=А2= ... Ап = А, то прямое произведение А1 х А2х … х Ап = Ап называется п-й степенью множества А.

Например, если рассмотреть все точки плоскости, то мож­но считать, что задано множество R2 = R x R; R представляет собой множество действительных чисел (координат, откладываемых на оси координат), а пары вида (а, b), где a, b ∊ R — координаты точек на плоскости. Говорят, что R2 — двумерное пространство (плоскость). Аналогично, можно рассматривать множество R3 — множество точек трехмерного пространства. При этом существенно, что положение точки на плоскости (в пространстве) однозначно определяется ее координатами.

Представление точек плоскости через координаты было впервые предложено Декартом, поэтому прямое произведе­ние часто называют декартовым.

 

Контрольные вопросы.

1. Напишите обозначение основных символов, используемых в теории множеств

2. Что такое множество? Как его обозначить? Пример

3. Как можно задать множество? Пример

4. Какое множество называют счетным? Какое – пустым? Пример

5. Что такое подмножество? Пример

6. Сформулируйте основные свойства счетных множеств

7. Какие соотношения (действия) между множествами вы знаете, перечислите их. Как они обозначаются?

8. Какое множество можно назвать универсальным? Пример

9. Какие операции (из аналогичных арифметических) нельзя производить с множествами?

10. Что такое диаграмма Эйлера? Проиллюстрируйте с помощью диаграмм Эйлера объединение и пересечение трех множеств

11. Дайте определение декартова произведения множеств (прямое произведение множеств). Пример

12. Поясните термин «мощность множества»

 

Лекция № 2

Тема: «Операции с множествами»

План лекции

1. Основные тождества алгебры множеств

2. Алгоритм доказательства тождеств

3. Примеры

 

1. Основные тождества алгебры множеств

Для любых подмножеств А, В и С универсального множества U выполняются следующие тождества.

1. а) A U В = В U А (коммутативность U);

б) А ∩ В = В ∩ А (коммутативность ∩).

2. а) A U (В U С) = (A U В) U С (ассоциативность U);

б) А ∩ (В ∩ С) = (А ∩ В) ∩ С (ассоциативность ∩).

3. а) А U (В ∩ С) = (А U В) ∩ (А U С) (дистрибутивность U относительно ∩);

б) А ∩ (В U С) = (А ∩ В) U (А ∩ С) (дистрибутивность ∩ относительно U).

4. а) A U 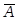= U; б) А ∩ = ∅

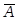5. а) A U ∅ = А; б) А ∩ U = А.

6. а) A U А = А; б) А ∩ А = А.

7. а) A ∪ U = U; б) А ∩ ∅ = ∅ .

8. a) 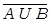= 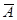∩ 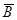(закон двойственности — закон де Моргана);

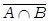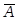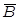б) = U (закон двойственности — закон де Моргана).

9. а) A U (А ∩ В) = А (закон поглощения).

б) А ∩ (А U В) = А (закон поглощения).

Справедливость тождества устанавливается с помощью принципа равнообъемности: показывается, что множества, в левой и правой частях тождества, состоят из одних и тех же элементов.

Введенные тождества принято называть булевыми — по имени автора, впервые их доказавшего.

Джорж Буль (1815—1864) — английский математик, один из основоположников математической логики — науки, которая состоит в том. Чтобы такие тонкие функции человеческого мышления, как доказательство утверждений, проверка гипотез, разработка теорий, связанных с проведением логических рассуждений, сделать «механическими». Было можно выполнять «автоматически» по заданному алгоритму. В работе «Исследование законов мышления» Буль сформулировал основные положения алгебры логики.

Введенная система тождеств полна в том смысле, что любое соотношение между множествами является следствием булевых тождеств.

Составим произведения множеств, составленные из исход­ных множеств и их дополнений так, чтобы каждое встреча­лось только один раз (назовем такие произведения конституенты (составляющие)).

Для доказательства любого тождества в алгебре множеств удобно использовать следующий алгоритм:

Ø представить рассматриваемое множество (на основе исполь­зования введенных операций и булевых тождеств) в виде суммы конституент. Для этого:

а) добиться, чтобы знаки отрицания стояли только над буквами, обозначающими множества;

б) раскрыть скобки и приходим к выражению вида «сум­ма произведений»;

в) одинаковые множители в произведении заменить од­ним. Произведение, содержащее множество и его допол­нение, удалить;

г) добиться, используя соотношение К = КАі + К 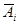что­бы все произведения состояли из одного и того же числа сомножителей;

д) если некоторое слагаемое входит в сумму более одного раза, то оставить только одно;

Ø два множества равны в том и только в том случае, когда они составлены из одних и тех же конституент.

 

Примеры:

 

Рассмотрим операцию дополнения множества, являющуюся пересечением множеств А и В. Покажем, что ее результат совпадает с объединением дополнений этих множеств.

Запишем ход решения задачи по действиям

1.

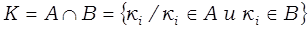
2.

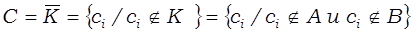
3.

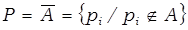
4.

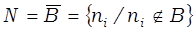
5.

 

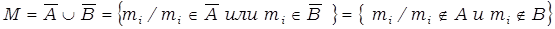
Свойства элементов множеств М и С одинаковы, следовательно, эти множества равны.

 

Решение задачи с помощью диаграмм Эйлера-Венна.

 

 

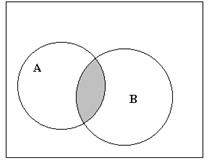
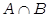
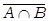
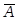
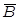
Контрольные вопросы.

1. Сформулируйте понятие включения множеств. Пример

2. Сформулируйте понятие суммы множеств. Пример

3. Сформулируйте понятие произведения множеств. Пример

4. Сформулируйте понятие вычитания множеств. Пример

5. Сформулируйте понятие дополнения множества. Пример

6. Сформулируйте основные тождества коммутативности алгебры множеств

7. Сформулируйте основные тождества ассоциативности алгебры множеств

8. Сформулируйте основные тождества дистрибутивности алгебры множеств

9. Сформулируйте основные законы двойственности алгебры множеств

10. Сформулируйте основные законы поглощения алгебры множеств

11. Сформулируйте основные тождества алгебры множеств: объединения множества с пустым множеством, универсальным и своим дополнением

12. Сформулируйте основные тождества алгебры множеств: пересечения множества с пустым множеством, универсальным и своим дополнением


Лекция № 3

Тема: «Отображения, отношения, функции»

План лекции

1. Понятие отображения

2. Типы отображений. Примеры

3. Понятие функции

 

1. Понятие отображения

 

Понятия отображения и функции — одни из самых важ­ных в математике. Они выражают зависимость одних перемен­ных величин от других. При этом слово «величина» может нести различную смысловую нагрузку. Это может быть эле­мент любого множества, число, вектор и т. д.

Отображение множества X во множество Y определяется тем, что каждому элементу х ∈ X ставится в соответствие некоторый элемент у ∈ Y.

Для обозначения отображения f множества X во множе­ство Y используется запись f: X →Y или (что более привыч­но) у = f(x).

Например, всякая нумерация счетного множества являет­ся его отображением на множество N.

Так как отображение может быть истолковано как соответствие, то для того чтобы показать, что данный элемент хпоставлен в соответствие элементу у, пишут: у = f(x) и говорят, что у есть образ элемента х при данном отображении f .

Совокупность тех элементов х ∈ X, образом которых является элемент у ∈ Y, называется прообразом элемента Y и обозначается

f-1(у)

Пусть X' ⊂ X, Y' ⊂ Y, тогда подмножество

f (X') : = { f(x)\x ∈ X'} ⊂ Y – образ подмножества X' при отображении f, а подмноже­ство f-1(У’): = { x\f(x) ∈ Y'} ⊂ X' – полный прообраз подмножества Y'.

 

2. Типы отображений. Примеры

Если каждый элемент множества Y имеет прообраз, при отображении множества X в Y, то отображение называется сюръективным (сюръекция).

Отображение f называется инъективным (инъекция), если для каждого элемента у ∈ У существует не более одного прообраза, т. е.

Если отображение f сюръективно и инъективно, то оно называется биективным (взаимно-однозначным), биекция.

Понятие биективного отображения не предполагает, что множества Хи Y конечны.

Пример биективного отображения между бесконечными множествами:

множество X состоит из все целых чисел, Y— множество натуральных чисел:

X = {0, -1, 1, -2, 2, ...}, Y = {1, 2, 3, 4, 5, ...}.

Рассмотрим, например, три функции, отображающие множество R действительных чисел само на себя,

1) функция f1(x) = ех инъективна, но не сюръективна;

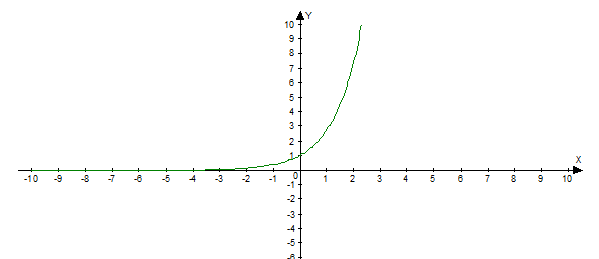
2) функция f 2(х) = х (х2 — 1) сюръективна, но не инъективна;

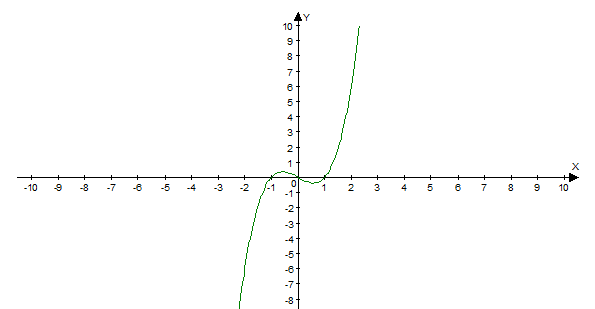
3) функция f3(x) = Зх + 1 биективна.

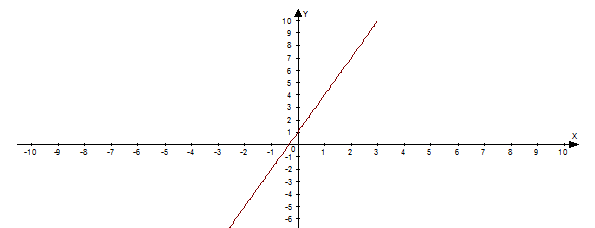
Отношение на множестве. Если в декартовом квадрате 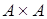некоторого множества A выделено какое-либо подмножество 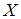, то говорят, что на A задано отношение (или бинарное отношение). Если для некоторых элементов 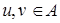имеет место включение 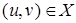, то говорят, что 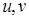находятся в отношении .

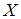Если 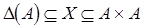, то отношение 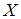называется рефлексивным.

Если отношение 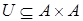таково, что из включения 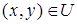обязательно следует, что 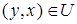, то отношение 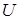называется симметричным.

Если отношение 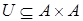таково, что из включени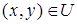й и 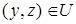следует, что 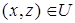, то отношение 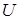называется транзитивным.

Если отношение 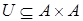таково, что из одновременных включени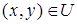й и 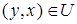следует, что 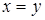, то отношение называется антисимметричным.

Полагают по определению, что пустое множество является отношением одновременно рефлексивным, симметричным, антисимметричным и транзитивным.

Если отношение рефлексивно, транзитивно и симметрично, то оно называется эквивалентностью. Если же отношение одновременно рефлексивно, транзитивно и антисимметрично, то оно называется частичным порядком.

Если 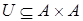- частичный порядок на множестве A и 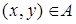, то говорят, что элементы 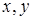сравнимы относительно 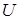или просто сравнимы; иногда пишут в этом случае 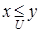или просто .

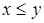С точки зрения отображений два множества называются количественно-эквивалентными (или просто эквивалентными), если между ними можно установить биективное отображение.

Подмножество F ⊂ A x B называется функцией, если для любого элемента х, х∈А, найдется не более одного элемента у∈В вида (х,у) ∈ F. При этом, если для любого элемента х имеется один элемент у вида (х,у) ∈ F, то функция называется всюду(полностью) определенной, в противном случае – частично определенной (недоопределенной).

Множество А – область определения функции F, множество В – область значений функции F.

Количество аргументов определяет местность функции.

Через теорию множеств введем понятие функции.

Подмножество FÎMx x My называется функцией, если для каждого элемента хÎMx найдется yÎМу не более одного.

(x;y)ÎF, y=F(x).

Соответствие между аргументом и функцией можно изобразить с помощью диаграммы Венна:

       
 
   
 

 


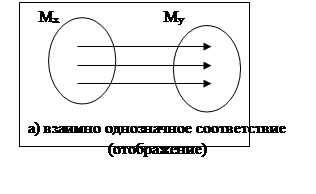Между множествами MX и MY установлено взаимноодназночное соответствие, если каждому хÎMX соответствует 1 элемент yÎMY и обратное справедливо.


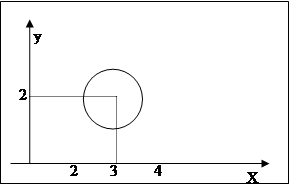
Пример: 1) (х,у) в круге

2) x = sinx

R→ R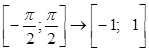

 

 

Обратное отображениеf-1: У→Х, определяется для биекции

f : Х → У следующим образом:

если f(х) = у, то f-1(у) = х;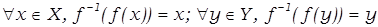

Например: взаимно-однозначное отображение R на R’, где R’ – множество всех положительных действительных чисел, определяемое формулой у = ех. Обратным к нему будет отображение х = ln y

Пусть рассмотрим упорядоченные пары (х,у), х ∈ X, у ∈ Y, т.е. декартово произведение Х х У множеств Х и У. Тогда отображение f : Х → У порождает в множестве Z = Х х У подмножество { х, f(x)\x ∈ X}, которое называется графиком отображения f.

График полностью определяет отображение.

Контрольные вопросы.

1. Дайте определение отображения множества А во множество В. Пример

2. Что такое сюръекция? Пример

3. Что такое инъекция? Пример

4. Что такое биекция? Пример

5. Дайте определение функции. Пример

6. Поясните термин «образ подмножества». Пример

7. Поясните термин «прообраз подмножества». Пример

8. Какие множества называются количественно-экви-валентными?

9. Как определяется обратное отображение? Пример

10. Какая функция называется всюду (полностью) определенной?

11. Что называют графиком отображения?

Лекция № 4

Тема: «Операции логики Буля»

План лекции

1. Понятие логики Буля

2. Операции логики Буля

3. Основные законы логики Буля

Понятие логики Буля

С точки зрения логики, вместо одной предметной переменной х удобно ввести две логические переменные х1 и х2. Областью определения х1 и х2 будут уже не числа натураль­ного ряда, а только два логических значения: 1 для истинного зна­чения и 0 для ложного.

Переменные х1 и х2 определяют некоторую логическую функцию: y = f (х1, х2).

На диаграммах Эйлера-Венна можно все возможные значения логических функций можно задавать с помощью четырех заштрихованных областей Сi:

С0 – элементы, которые не обладают свойствами множеств А и В

С1 – элементы, которые обладают свойствами множества А

С2 – элементы, которые обладают свойствами множества В

С3 – элементы, обладающие одновременно двумя свойствами множеств А и В

Между таблицами истинности и диаграммой Эйлера — Венна существует вза­имно однозначное соответствие. Поэтому число единиц для у всегда будет сов­падать с числом заштрихованных областей на диаграмме.

Операции логики Буля

1. Дизъюнкция – логическая связка «или/и», v — символ.

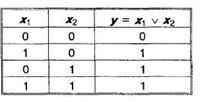
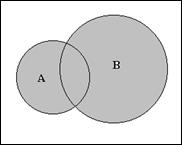Факт принадлежности элемента х множеству А обознача­ется как х ∈ А . Поэтому то, что х принадлежит А или/и В, выражается формулой:

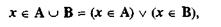
2. Конъюнкция - логическая связка «и», Ù — символ

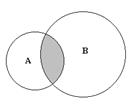То, что х принадлежит одновременно двум множествам А и В, можно представить выражением: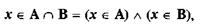

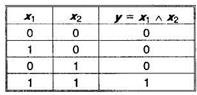
Если в табли­це истинности для конъюнкции (табл. 2) все нули заменить единицами, а все едини­цы — нулями, то в итоге получим табл. 1. Этот факт опре­деляет взаимную двойственность конъ­юнкции и дизъюнкции. Для любой логической операции можно найти двойственную.

3. Отрицание

Множество 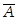дополняет множество А до фундаментального множества V (или 1); от­сюда название: дополнительное множество А или дополнение как опе­рация. Дополнение к логической переменной х, т.е. 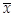(не-х), называется в логике чаще всего отрицанием х. После введения операций пересечения и дополнения все четыре области С, на диа­грамме Эйлера — Венна можно выразить следующим образом:

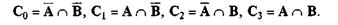
Путем объединения соответствующих областей С, можно представить любую множественную операцию, в том числе и само объединение:

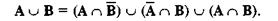
Все это распространяется и на логику:

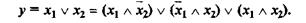
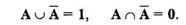
Аналогичные равенства выполняются и для логических функций, которые имеют соответствующие названия:

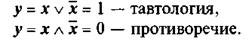
Тавтология — это всегда истинное логическое выражение, какое бы при этом значение ни принимала переменная х. Противоречие, напротив, всегда ложное выражение.

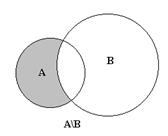4. Разность и импликация

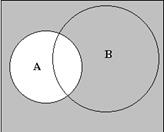Разностью между множествами А и В называется совокупность тех элементов множества А , которые не вошли в множество В.

Дополнением к разности служит импликация.

Таблицы истинности для разно­сти и импликации представлены табл.5 и табл. 6.

       
 
х1 х2 у = х1 - х2
     
     

 
   
х1 х2 у = х1 → х2

 
 

 

 


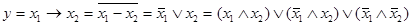
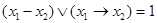
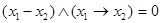
5. Дополнение объединения и пересечения до U.

Операции стрелка Пирса и штрих Шеффера

 

 

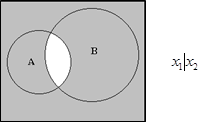
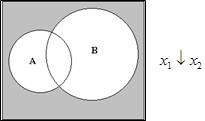
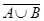
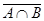
На языке логических формул это выражается так:

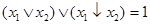для стрелки Пирса

 

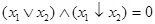
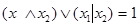для штриха Шеффера

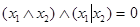
Таблицы истинности:

х1 х2

х1 х2

 

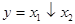
Из таблиц истинности для этих операций видно, что:

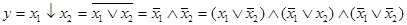
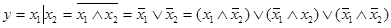
6. Симметрическая разность и эквивалентность

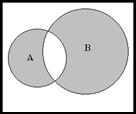
Симметрическая разность двух множеств А и В есть объединение двух разностей

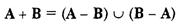
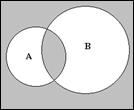
Эквивалентность определяется теми элементами множеств А и В, которые для них являются общими. Элементы, не входящие ни в А ни в В, тоже считаются эквивалентными.

у = х1 ~ х2

х1 х2 у = x1 ~ x2

 
Таблицы истинности

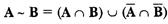
х1 х2 у = x1 + x2

 

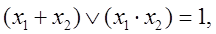
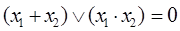
у = х1 ~ х2 =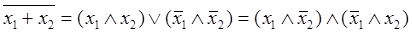

Основные законы логики Буля

В качестве основных законов логики Буля чаще других называют:

1) законы идемпотентности:

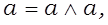
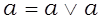
2) законы коммутативности:

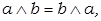
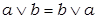
3) Законы ассоциативности:

;

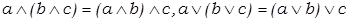4) Законы дистрибутивности:

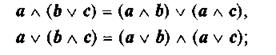
5) законы нуля и единицы:

;

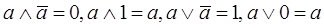6) законы поглощения:

,

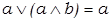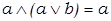
7) законы де Моргана:

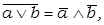
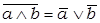
8) законы склеивания:

.

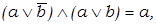
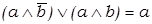Не все восемь законов независимы друг от друга. Так, например, закон идем­потентности можно получить из закона поглощения с использованием закона дистрибутивности:

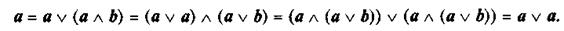
Закон поглощения может быть выведен из закона нуля и единицы:

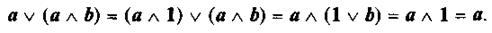
Закон идемпотентности относительно дизъюнкции непосредственно выводится из законов нуля и единицы:

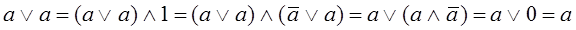
При доказательствах логических выражений мы должны всегда иметь в виду принцип двойственности. Так, вышеприведенная цепочка равенств для закона поглощения может быть представлена следующим образом:

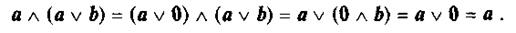
Итак, в качестве независимой системы законов можно выбрать законы: комму­тативности, ассоциативности, дистрибутивности, нуля и единицы.

В логике широко используются два подхода — аксиоматический и конструктивный. При аксиоматическом доказательстве используется жесткая система аксиом, состоящая, например, из четырех только что названных. Все остальные тождества необходимо представлять через эти законы. При конструктивном же доказательстве мы должны будем воспользоваться системой конструктов, примерами которых являются диаграмма Эйлера — Венна и таблица истинности.

 

Контрольные вопросы.

1. Какие формулы называются тавтологиями? Противоречиями? Пример

2. Что такое дизъюнкция? Как ее задать с помощью диаграмм Эйлера?

3. Что такое конъюнкция? Как ее задать с помощью диаграмм Эйлера?

4. Что такое разность? Как ее задать с помощью диаграмм Эйлера?

5. Что такое импликация? Как ее задать с помощью диаграмм Эйлера?

6. Что такое штрих Щеффера? Как его задать с помощью диаграмм Эйлера?

7. Что такое стрелка Пирса? Как ее задать с помощью диаграмм Эйлера?

8. Что такое симметрическая разность? Как ее задать с помощью диаграмм Эйлера?

9. Что такое эквивалентность? Как ее задать с помощью диаграмм Эйлера?

10. Что такое дизъюнкция? Как ее задать с помощью таблицы истинности?

11. Что такое конъюнкция? Как ее задать с помощью таблицы истинности?

12. Что такое разность? Как ее задать с помощью таблицы истинности?

13. Что такое импликация? Как ее задать с помощью таблицы истинности?

14. Что такое штрих Щеффера? Как его задать с помощью таблицы истинности?

15. Что такое стрелка Пирса? Как ее задать с помощью таблицы истинности?

16. Что такое симметрическая разность? Как ее задать с помощью таблицы истинности?

17. Что такое эквивалентность? Как ее задать с помощью таблицы истинности?

18. Сформулируйте основные тождества коммутативности логики Буля

19. Сформулируйте основные тождества ассоциативности логики Буля

20. Сформулируйте основные тождества дистрибутивности логики Буля

21. Сформулируйте основные законы двойственности логики Буля

22. Сформулируйте основные законы поглощения логики Буля

23. Сформулируйте основные тождества логики Буля: объединения множества с пустым множеством, универсальным и своим дополнением

24. Сформулируйте основные тождества логики Буля: пересечения множества с пустым множеством, универсальным и своим дополнением

 

Лекция № 5

Тема: «Формы представления булевых функций»

План лекции

1. Понятие логики Буля

2. Операции логики Буля

3. Основные законы логики Буля

 

Любую булеву функцию у = 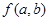можно представить как некоторую комбина­цию областей:

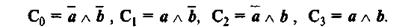
Тогда, в зависимости от значения функции и заданных Сi, которые в этом слу­чае мы будем именовать конституентами, получим шестнадцать логических операций:

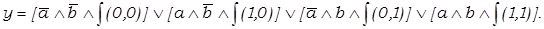
Подобная форма представления логических функций называется совершенной дизъюнктивной нормальной формой (СДНФ).

В логике Буля действует принцип двойственности, который гласит: при одно­временной замене символов 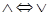и 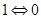все логические равенства остаются в силе. Поэтому нашу СДНФ можно представить несколько иначе:

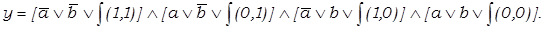
Эта форма представления называется совершенной конъюнктивной нормальной формой (СКНФ). Здесь уже конституенты представлены не в виде конъюнктов, как в СДНФ, а в виде дизъюнктов. Соединены же эти дизъюнкты конъюнкцией, отсюда и название — СКНФ.

Существует еще и третья форма — совершенная полиномиальная нормальная форма (СПНФ). Ее легко получить из СДНФ путем замены:

,

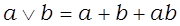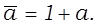
Поскольку конституенты не пересекаются (СiCj = 0), мы можем сразу же запи­сать (в СПНФ символ конъюнкции опускается):

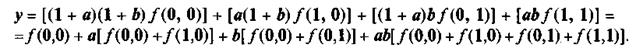
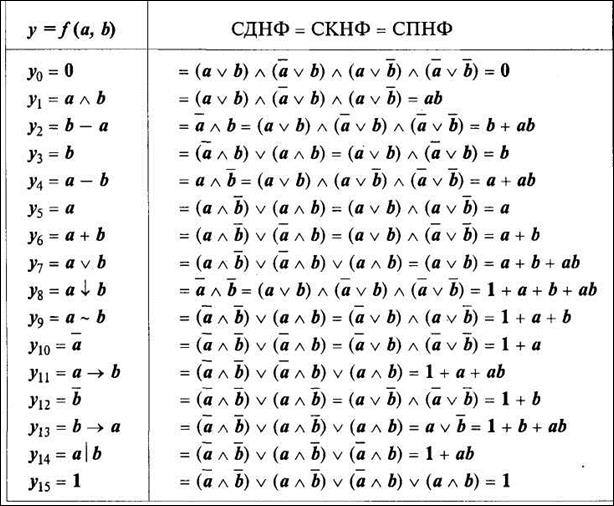В табл. 1.9 приведен полный список элементарных логических функций от двух аргументов и в трех совершенных формах — СДНФ, СКНФ и СПНФ. Совершенные формы представлений позволяют выразить аналитической формулой любую функцию, если известна ее таблица истинности.

Дата добавления: 2021-09-25; просмотров: 443;

Поиск по сайту:

Воспользовавшись поиском можно найти нужную информацию на сайте.

Поделитесь с друзьями:

Считаете данную информацию полезной, тогда расскажите друзьям в соц. сетях.
Poznayka.org - Познайка.Орг - 2016-2024 год. Материал предоставляется для ознакомительных и учебных целей.
Генерация страницы за: 0.099 сек.