Отношения между суждениями по истинности

При сопоставлении различных мнений по спорным вопросам и во многих других случаях важно знать о существовании определенных типов отношений между суждениями по истинности. Каждый тип отношений фиксирует определенную зависимость истинностного значения одного суждения от значения другого суждения. Устанавливая отношения между суждениями, мы должны исходить из того, могут ли быть эти суждения вместе истинными или не могут; могут ли они быть вместе ложными или нет; обусловливает ли истинность одного суждения истинность другого, означает ли ложность одного из них, что ложным должно быть и другое? Надо заметить, что подобного рода зависимости можно установить тогда, когда суждения имеют одни и те же термины и различаются по качеству или количеству. Такие суждения называются сравнимыми.

Среди сравнимых выделяют совместимые и несовместимые суждения. Если сравнимые суждения могут быть одновременно истинными, то они называются совместимыми. Несовместимыми называются такие сравнимые суждения, которые не могут быть одновременно истинными.

Совместимость бывает трех видов: равнозначность (эквиваленция), подчинение, частичное совпадение (субконтрарность). Отношения несовместимости подразделяются на противоположность (контрарность) и противоречие (контрадикторность). Указанные виды отношений (кроме равнозначности) принято изображать в виде схемы — логического квадрата (рис. 3.8).

А Противоположность Е

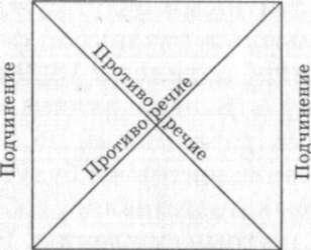
I Частичное совпадение Е

Рис. 3.8. Логический квадрат

Логический квадрат позволяет легче запоминать различные отношения, которые существуют между суждениями А, I, Е, О. На этой схеме буквы, обозначающие виды суждений (А, I, Е, О) помещаются в углах квадрата. Стороны и диагонали представляют собой отношения между суждениями. Теперь рассмотрим каждое из этих отношений.

Противоречие. В отношении противоречия находятся сужения, соединенные диагоналями логического квадрата, т.е. А и О, а также Е и I. Противоречащие суждения не могут быть одновременно истинными или одновременно ложными. Они всегда имеют разные значения истинности. Если одно из них истинно, то другое непременно ложно, и наоборот. Сравните следующие суждения: "Все студенты нашей группы сдали зачет по логике" и "Некоторые студенты нашей группы не сдали зачет по логике".

Противоположность. Это отношение существует между общеутвердительными (А) и общеотрицательными (Е) суждениями. Эти суждения не могут быть одновременно истинными, но они могут быть одновременно ложными. Убедимся в этом на примере: "Все студенты нашей группы сдали зачет по логике" (А), "Ни один студент нашей группы не сдал зачет по логике" (Е). Если допустить, что суждение А истинное, то в этом случае суждение Е будет только ложным. Если же соотнести эти суждения с ситуацией, при которой лишь некоторые студенты данной группы имеют зачет по логике, то в данном случае окажется, что и А, и Е будут ложными. Следовательно, зная, что одно из противоположных суждений ложное, мы не можем только на этом основании установить истинностное значение другого (другое суждение может быть как истинным, так и ложным).

Равнозначность. Сравнимые суждения считаются равнозначными, если они всегда принимают одинаковые логические значения. Равнозначными будут суждения, которые выражают одну и ту же мысль в различной форме. Это может быть в случае, когда термины (или один из них) выражены в суждениях разными по содержанию, но равнообъемными понятиями. Например: "Автор романа "Война и мир" родился в 1829 году", "Л.Н. Толстой родился в 1829 году". В этих высказываниях субъекты выражены различными по форме, но равнообъемными понятиями. Еще один пример: «Юрий Гагарин – первый космонавт» и «Юрий Гагарин первым совершил полет в космическое пространство». Равнозначными будут также такие два суждения, одно из которых представляет собой отрицание суждения, противоречащего другому суждению. Например, суждение "Все врачи имеют медицинское образование" будет равнозначно суждению "Неверно, что некоторые врачи не имеют медицинского образования". Первое из приведенных суждений является общеутвердительным (А), второе представляет собой отрицание частноотрицательного суждения (не-О). Следовательно, А равнозначно не-О (А ≡ не-О). Точно также О≡ не-А, I≡ не-Е, Е ≡ не-I.

Подчинение. В отношении подчинения находится суждения А и I, а также Е и О. Суждение А является подчиняющим по отношению к суждению I, которое рассматривается как подчиненное. Соответственно, Е — подчиняющее, а О — ему подчиненное.

Отношения подчинения характеризуются тем, что: 1) из истинности подчиняющего суждения следует с необходимостью истинность подчиненного; 2) из ложности подчиненного вытекает ложность подчиняющего; 3) из истинности подчиненного не следует истинность подчиняющего; 4) из ложности подчиняющего не следует ложность подчиненного.

Частичное совпадение). Данный вид отношения существует между частноутвердительными (I) и частноотрицательными (О) суждениями. Оба этих суждения могут быть одновременно истинными, но не могут быть одновременно ложными. Если одно из них ложно, то другое непременно истинное. Рассмотрим в качестве примера два суждения: "Некоторые студенты нашей группы сдали зачет по логике" (I), "Некоторые студенты нашей группы не сдали зачет по логике" (О). В ситуации, когда, предположим, 15 человек из 20 сдали зачет по логике, оба эти суждения окажутся истинными. А теперь попытайтесь представить себе ситуацию, при которой оба эти суждения оказались бы ложными... Ложность, например, суждения О "Некоторые студенты нашей группы не сдали зачет по логике" означает, что в группе нет таких студентов, которые бы не сдали зачет. Следовательно, суждение I "Некоторые студенты нашей группы сдали зачет по логике" будет истинным. Если же нам известно, что одно из этих суждений истинно, то на этом основании определить значение другого суждения нельзя. Оно может оказаться как истинным, так и ложным.